Коэффициент конкордации: пример расчета и формула. Что такое коэффициент конкордации

Коэффициент конкордации: пример расчета и формула. Что такое коэффициент конкордации?

При экспертной оценке, к примеру, оценке конкурентоспособности продукции, нужно, как в хоть какой научной работе, провести статистическую обработку данных. Крайняя начинается с определения согласованности воззрений профессионалов, числовым выражением которой является коэффициент конкордации.

Для чего же нужна оценка согласованности воззрений профессионалов?

Эта оценка нужна, сначала, поэтому, что представления профессионалов могут очень расходиться по оцениваемым характеристикам. Вначале оценку проводят по ранжированию характеристик и присвоению им определенного коэффициента значимости (весомости). Несогласованное ранжирование приводит к тому, что данные коэффициенты будут статистически недостоверными. Представления профессионалов при их нужном количестве (наиболее 7-10) должны быть распределены по нормальному закону.

Понятие о коэффициенте конкордации

Итак. Согласованность — это конкордация. Коэффициент — это безразмерная величина, показывающая отношение в общем случае дисперсии к наибольшей дисперсии. Обобщаем эти понятия.

Коэффициент конкордации — это число от 0 до 1, показывающее согласованность воззрений профессионалов при проведении ранжирования каких-либо параметров. Чем поближе это значение к 0, тем согласованность считается наиболее низкой. При величине данного коэффициента наименее 0,3 представления профессионалов числятся несогласованными. При нахождении величины коэффициента в спектре от 0,3 до 0,7 согласованность считается средней. При величине наиболее 0,7 согласованность принимается как высочайшая.

Случаи использования

При проведении статистических исследовательских работ могут возникать ситуации, в каких объект может характеризоваться не 2-мя последовательностями, которые статистически обрабатываются при помощи коэффициента конкордации, а несколькими, которые подходящим образом ранжируют при помощи профессионалов, имеющих однообразный уровень профессионализма в определенной области.

Согласованность ранжирования, осуществленного профессионалами, нужно определять для доказательства корректности догадки о том, что специалисты создают относительно четкие измерения, что дозволяет сформировывать разные группировки в экспертных группах, которые обуславливаются почти во всем человечьими факторами, до этого всего таковыми, как различие взглядов, концепций, различными научными школами, нравом проф деятельности и т. д.

Короткая черта способа рангов. Его плюсы и недочеты

При осуществлении ранжирования употребляется способ рангов. Его суть состоит в том, что любому свойству объекта присваивается собственный определенный ранг. При этом каждым профессионалом, входящим в экспертную группу, этот ранг присваивается без помощи других, в итоге чего же возникает необходимость обработки этих данных с целью выявления согласованности воззрений профессионалов. Осуществляется этот процесс с помощью расчета коэффициента конкордации.

Основное достоинство способа рангов — простота воплощения.

Главными недочетами способа являются:

• маленькое количество объектов ранжирования, так как при превышении их количества 15-20, становится тяжело присвоить конкретные ранговые оценки;
• на основании использования данного способа остается открытым вопросец о том, как далековато по значимости находятся исследуемые объекты друг от друга.

При использовании данного способа нужно учесть, что рейтинги основываются на какой-нибудь вероятностной модели, потому использовать их необходимо с осторожностью, беря во внимание область внедрения.

Ранговый коэффициент конкордации Кендалла

Употребляется с целью определения зависимости меж количественными и высококачественными признаками, характеризующими однородные объекты и ранжированными по одному принципу.

Определение данного коэффициента делается по формуле:

S — сумма разностей меж числом последовательностей и числом инверсий по второму признаку;

n — количество наблюдений.

• Осуществляется ранжирование величин х в порядке или убывания, или возрастания.
• Величины у располагают в том порядке, в каком они соответствуют величинам х.
• Для всякого следующего ранга у определяют, сколько превосходящих его значений рангов идет за ним. Их складывают и рассчитывают меру соответствия последовательностей рангов по x и y.
• Аналогично рассчитывают количество рангов у с наименьшими значениями, которые также складывают.
• Складывают количество рангов с превосходящими значениями и количество рангов с наименьшими значениями, в итоге получают величину S.

Данный коэффициент указывает зависимость меж 2-мя переменными, и почти всегда именуется ранговым коэффициентом корреляции Кендалла. Такую зависимость можно изобразить графически.

Определение коэффициента

Как это делается? В случае, если количество ранжируемых признаков либо причин превосходит 2, употребляют коэффициент конкордации, который, по собственной сущности, представляет собой множественный вариант ранговой корреляции.

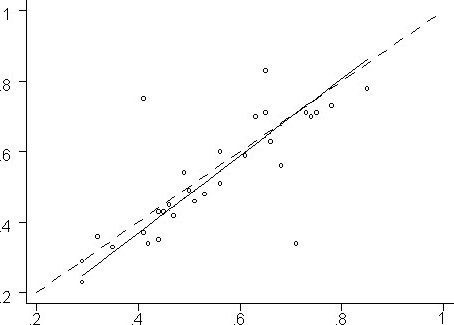
Будьте внимательны. Расчет коэффициента конкордации основан на отношении отличия суммы квадратов рангов от средней суммы квадратов рангов, умноженного на 12, к квадрату профессионалов, умноженных на разницу меж кубом числа объектов и числом объектов.

Метод расчета

Для того чтоб осознать, откуда берется число 12 в числителе расчетной формулы, поглядим на метод определения.

Для каждой строчки с рангами определенного профессионала рассчитывается сумма рангов, которая представляет собой случайную величину.

Коэффициент конкордации в общем виде определяется как отношение оценки дисперсии (D) к наибольшему значению оценки дисперсии (D_max). Приведем поочередно формулы определения этих величин.

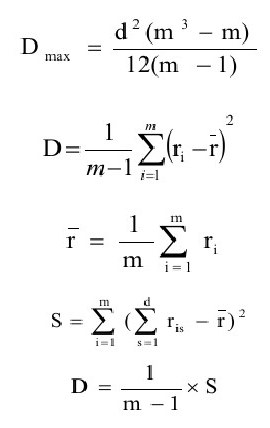
где r_ср — оценка математического ожидания;

m — число объектов.

Подставляя приобретенные формулы в отношение D к D_max получаем окончательную формулу коэффициента конкордации:

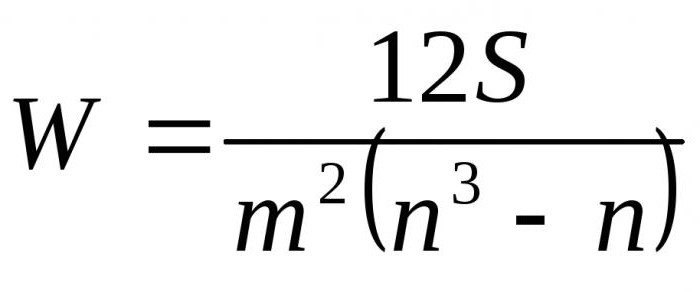
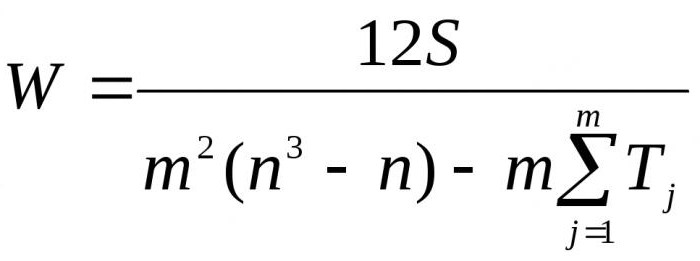
Тут m — число профессионалов, n — число объектов.

1-ая формула употребляется для определения коэффициента конкордации, если нет связанных рангов. 2-ая формула употребляется в этом случае, если связанные ранги имеются.

Итак, окончен расчет коэффициента конкордации. Что далее? Приобретенное значение оценивается на значимость при помощи коэффициента Пирсона умножением данного коэффициента на количество профессионалов и на число степеней свободы (m-1). Приобретенный аспект сравнивается с табличным значением, и при превышении значения первого над крайним, молвят о значимости исследуемого коэффициента.

В случае наличия связанных рангов расчет аспекта Пирсона несколько усложняется и делается последующим отношением: (12S)/(d(m 2 +m)-(1/(m-1))x(T_s1 +T_s2 +T_sn)

Пример

Представим, что экспертным способом оценивается конкурентоспособность сливочного масла, реализуемого в розничной торговой сети. Приведем пример расчета коэффициента конкордации. До этого, чем оценить конкурентоспособность, нужно проранжировать потребительские характеристики данного продукта, которые участвуют в проводимой оценке. Представим, что в качестве таковых параметров будут выступать последующие: вкус и запах, смесь и наружный вид, цвет, упаковка и маркировка, содержание жира, торговое наименование, производитель, стоимость.

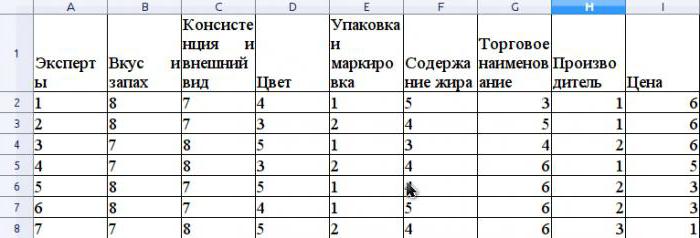
Примем, что в состав экспертной группы входят 7 профессионалов. На рисунке продемонстрированы результаты ранжирования данных параметров.

Среднее значение r рассчитывается как среднее арифметическое и составит 31,5. Для нахождения S суммируем квадраты различий меж r_is и r средним, согласно приведенной ранее формулы, и определим, что величина S составляет 1718.

Рассчитаем коэффициент конкордации по формуле без использования связанных рангов (связанными могли быть ранги в случае, если у 1-го и такого же профессионала по различным свойствам встречались бы однообразные ранги).

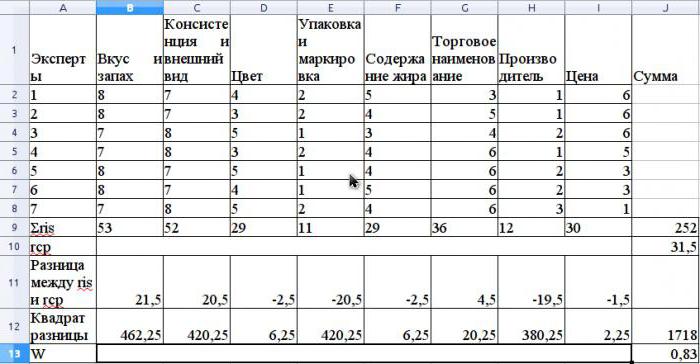
Величина данного коэффициента составит 0,83. Это свидетельствует о мощной согласованности воззрений профессионалов.

Проверим ее значимость по аспекту Пирсона:

7 х 0,83 х (8-1) = 40,7.

Табличный аспект Пирсона при 1% уровне значимости составляет 18,5, а при 5% — 14,1. И то, и другое числа — меньше расчетного значения, как следует, при уровне значимости 1% принимается весомым рассчитанный коэффициент конкордации.

Пример показывает простоту и доступность расчета для хоть какого человека, обладающего основами математических расчетов. Для их облегчения можно пользоваться формами электрических таблиц.

В заключение

Таковым образом, коэффициент конкордации указывает согласованность воззрений нескольких профессионалов. Чем далее он от 0 и поближе к 1, тем представления наиболее согласованные. Подтверждаться данные коэффициенты должны расчетом аспекта Пирсона.

Как применять функцию IMPORTRANGE в Гугл Таблицах (примеры)

Доступ к данным из одной книжки в другую в Гугл Таблицах не так прост, как для хоть какого другого программного обеспечения для работы с электрическими таблицами. В главном это соединено с онлайн-характером Гугл Таблиц.

И это имеет смысл, беря во внимание трудности сохранности данных.

Но Гугл дозволяет для вас получать доступ и применять данные из наружного рабочего листа, если у вас есть соответственное разрешение и доступ. Эта возможность обеспечивается функцией IMPORTRANGE .

Если вы когда-либо лицезрели вызов функции IMPORTRANGE ранее, вы, может быть, испугались (на 1-ый взор) ее длины и трудности.

Но, если честно, её синтаксис намного проще, чем кажется. В этом руководстве мы наиболее тщательно разглядим функцию IMPORTRANGE и усвоим, как она работает, на ординарном примере.

Синтаксис функции IMPORTRANGE

Синтаксис функции IMPORTRANGE :

Функция воспринимает два параметра:

• spreadsheet_url: это URL-адрес начальной электрической таблицы.
• range_string: это строчка, содержащая информацию о спектре ячеек для импорта.

Разберемся с этими параметрами незначительно подробнее.

URL таблицы либо Ключ книжки

Это 1-ый параметр функции IMPORTRANGE. Он содержит URL-адрес электрической таблицы либо ключ Гугл книжки, из которой вы желаете выполнить импорт.

Ниже вы сможете отыскать URL-адрес Гугл Таблиц.

И вы также сможете применять ключ книжки заместо использования всего URL-адреса в функции IMPORTRANGE.

Этот параметр обычно представляет собой строковое значение. Он может содержать URL-адрес начальной таблицы (заключенный в двойные кавычки) либо ссылку на ячейку, содержащую URL-адрес начальной электрической таблицы (без двойных кавычек).

URL-адрес электрической таблицы — это все положение, которое вы видите в адресной строке браузера, когда открыта начальная электрическая таблица.

1-ая часть URL-адреса — это главный URL-адрес Гугл Таблиц. За ней следует папка «d», за которой следует вправду большая строчка буквенно-цифровых знаков. Это ключ книжки либо идентификатор, который электрические таблицы Гугл употребляют для идентификации книжки.

Чтоб указать 1-ый параметр функции IMPORTRANGE, вы сможете применять полный URL-адрес электрической таблицы либо лишь ее ключ. Или 1-го довольно, чтоб идентифицировать электрическую таблицу, из которой вы желаете импортировать.

Строчка спектра

Строчка спектра — это 2-ой параметр функции IMPORTRANGE. Это также строковое значение и имеет последующий формат:

Видите ли, range_string состоит из 2-ух частей:

• sheet_name: это имя электрической таблицы, из которой вы желаете импортировать данные.
• range: это спектр ячеек, который вы желаете импортировать из начального листа. Этот компонент быть может ссылкой на спектр ячеек, одну ячейку либо именованный спектр.

Направьте внимание, что компонент sheet_name был представлен в квадратных скобках, поэтому что эта часть range_string является необязательной. Если вы не предоставите этот компонент, IMPORTRANGE по дефлоту импортирует 1-ый лист обозначенной книжки.

Вот несколько примеров строк спектра:

• «MySheet! A1: B10»: схожая строчка range_string употребляется, когда вы желаете импортировать ячейки от A1 до B10 из рабочего листа с именованием «MySheet».
• «A1: B10»: схожая строчка range_string употребляется, когда вы желаете импортировать ячейки от A1 до B10 с первого листа в начальной книжке.
• «MySheet! A5»: схожая строчка range_string употребляется, когда вы желаете импортировать лишь одну ячейку, A5, из рабочего листа с именованием «MySheet».

Пример — импорт спектра ячеек из другого листа

Чтоб показать, как применять функцию IMPORTRANGE, давайте попробуем импортировать ячейки с A1 по B7 из листа с именованием «Сотрудники» (англ. Employees), принадлежащего наружной книжке.

Вот шаги, которые для вас нужно выполнить:

• Откройте книжку, содержащую начальную электрическую таблицу (в нашем примере «Сведения о сотруднике 2020»).
• В адресной строке браузера вы сможете узреть URL-адрес книжки. Вы сможете избрать весь URL-адрес (как показано на изображении 1) либо избрать лишь ключ книжки (как показано на изображении 2).
  
• Скопируйте избранный URL-адрес либо ключ книжки, нажав CTRL + C на клавиатуре.
• Потом откройте мотивированную книжку.
• Щелкните ячейку, в какой должен отображаться спектр импортированных ячеек. В нашем примере мы желаем начать показывать ячейки начиная с A1.
• Введите формулу: =IMPORTRANGE(“<<url_here>>”,”<<source_sheet_name_here>>!<<range_here>>”).Replace <<url_here>>, <<source_sheet_name_here>> and <<range_here>> with the appropriate values. In our case, we will enter =IMPORTRANGE(“1Hw9qK3r4egNP7EHsYH2kcpBOAdGn64iW-WEIZ59rtF4″,”Employees!A1:B7”)
• Нажмите кнопку возврата.
• Дайте ему время на обработку.
• При первом использовании функции IMPORTRANGE вы получите # REF (ССЫЛКУ), как показано ниже:
• При наведении указателя мыши на ячейку вы получите запрос, спрашивающий, желаете ли вы разрешить доступ к листу.
• Нажмите на клавишу с надписью «Разрешить доступ».
• Сейчас вы должны узреть собственный спектр ячеек из начального листа, отображаемый в хотимой точке на мотивированном листе.

Примечание. Вы получите ошибку #REF (с шага 9) лишь при первом импорте из начального листа. В последующий раз, когда вы воспользуетесь данной функцией, она больше не будет показывать эту ошибку и запрашивать разрешение. Этот доступ остается в силе до того времени, пока юзер, предоставивший доступ, не будет удален из источника.

Также принципиально убедиться, что на мотивированном листе довольно пустых ячеек для размещения результата формулы.

Таковым образом, функцию IMPORTRANGE можно применять для доступа к данным из остальных книжек. Это становится в особенности полезным, когда вы желаете собрать данные из нескольких книжек на одном листе.

К примеру, при помощи IMPORTRANGE вы сможете импортировать данные о сотрудниках из различных филиалов компании в один сводный лист.

Мы возлагаем надежды, что нам удалось посодействовать для вас осознать, что делает функция IMPORTRANGE и как ее применять. Мы советуем для вас испытать это на для себя и убедиться, как это комфортно и сберегает время.

Ранг ако формула

За да класирате елементи в списък, използвайки един либо повече аспекты, сможете да използвате функцията COUNTIFS. В показания пример формулата в E5 е:

където «групи» е наименованият спектр C5: C14, а «резултати» е наименованият спектр D5: D14. Резултатът е ранг за всеки човек в собствената му група.

Забележка: въпреки че данните са сортирани по групи на екранната снимка, формулата ще работи добре с несортирани данни.

Обяснение

Въпреки че Excel има функция RANK, няма функция RANKIF, която да изпълнява условен ранг. Сможете обаче лесно да създадете условен RANK с функцията COUNTIFS.

Функцията COUNTIFS може да изпълнява условно броене, като използва два либо повече аспекта. Критериите се въвеждат в двойки обхват / аспекты. В този вариант първият аспект ограничава броя до една и съща група, като използва имената на групите от диапазони (C5: C14):

Това {само по себе} си ще върне общия брой членове на групата в група «А», което е 5.

Вторият аспект ограничава броя до само резултати, по-големи от «текущия резултат» от D5:

Двата аспекта работят заедно, за да преброят редове, където групата е A и резултатът е по-висок. За първото име в списъка (Хана) няма по-високи резултати в група А, така че COUNTIFS връща нула. На следващия ред (Едуард) има три резултата в група А по-високи от 79, така че COUNTIFS връща 3. И така нататък.

За да получим правилен ранг, ние просто добавяме 1 към номера, върнат от COUNTIFS.

Обратен ред на ранга

За да обърнете порядъка на класиране и класиране по ред (т.е. най-малката стойност е класирана # 1), просто използвайте оператора по-малко от ():

Заместо да отчита резултати, по-големи от D5, тази версия ще отчита резултати по-малки от стойността в D5, ефективно обръщайки реда на ранга.

Дубликати

Подобно на функцията RANK, формулата на тази страничка ще присвоява дублирани стойности със същия ранг. К примеру, ако на конкретна стойност е присвоен ранг 3 и има два екземпляра на стойността в данните, които се класират, и двата екземпляра ще получат ранг 3, а следващият присвоен ранг ще бъде 5. Да имитира поведението на функцията RANK.AVG, която би присвоила среден ранг 3,5 в такъв вариант, сможете да изчислите «корекционен фактор» с формула като тази:

Резултатът от тази формула по-горе може да се добави към първоначалния ранг, за да се получи среден ранг. Когато дадена стойност няма дубликати, горният код връща нула и няма ефект.