BI — это просто
Функции деления в DAX: DIVIDE, QUOTIENT и MOD для Power BI и Power Pivot
Содержание статьи: (кликните, чтоб перейти к соответственной части статьи):
 Приветствую Вас, дорогие друзья, с Вами Будуев Антон. В данной статье мы побеседуем о том, как в Power BI (Power Pivot) защититься от ошибки деления на 0. Также, о том, как из общей суммы секунд вычислить соответственное число часов, минут и секунд? А если гласить конкретнее, то разберем функции деления в DAX: DIVIDE (деление на ноль), QUOTIENT (целочисленное деление) и MOD (остаток от целочисленного деления).
Приветствую Вас, дорогие друзья, с Вами Будуев Антон. В данной статье мы побеседуем о том, как в Power BI (Power Pivot) защититься от ошибки деления на 0. Также, о том, как из общей суммы секунд вычислить соответственное число часов, минут и секунд? А если гласить конкретнее, то разберем функции деления в DAX: DIVIDE (деление на ноль), QUOTIENT (целочисленное деление) и MOD (остаток от целочисленного деления).
Для Вашего удобства, рекомендую скачать «Справочник DAX функций для Power BI и Power Pivot» в PDF формате.
Если же в Ваших формулах имеются какие-то ошибки, препядствия, а результаты работы формул повсевременно не те, что Вы ждете и Для вас нужна помощь, то записывайтесь в бесплатный экспресс-курс «Резвый старт в языке функций и формул DAX для Power BI и Power Pivot».
Также, подписывайтесь на наши социальные сети. Поэтому что конкретно в их, Для вас будут доступны оперативно и любой денек наши животрепещущие фишки, секреты, выработки, примеры, кейсы, полезные советы, видео и статьи по темам сквозной BI аналитики (Power BI, DAX, Power Pivot, Excel…): Вконтакте, Инстаграм, Фейсбук, YouTube.
DAX функция DIVIDE в Power BI и Power Pivot
DIVIDE () — производит деление с обработкой ошибки «деление на 0». Обработка ошибки заключается в выводе альтернативного результата в случае появления ситуации деления на ноль.
Где, кандидатура — (необязательный параметр) значение, которое необходимо вывести в случае ошибки деления на ноль (0). По дефлоту выводится пустое значение BLANK ().
Пример формулы на базе DAX функции DIVIDE.
В Power BI Desktop имеется начальная таблица «Реклама», содержащая по каждой дате издержки на рекламу и прибыль, полученную от продаж с данной нам рекламы:
Задачка — сделать в Power BI меру расчета коэффициента ROI (окупаемости издержек на рекламу). Данный коэффициент рассчитывается как сумма всей прибыли деленная на сумму всех издержек.
Сумму значений мы можем высчитать с помощью DAX функции SUM.
В итоге, формула расчета ROI будет таковой:
Другими словами, мы сложили всю прибыль, сложили все издержки и потом разделили сумму прибыли на сумму издержек.
Как бы, все отлично, но, если мы вынесем эту меру в отчеты Power BI и поглядим ROI по денькам, то в визуализации в одной из строк будет отображаться непонятное слово «Бесконечность»:
А все дело в том, что у нас произошла ошибка деления на ноль — прибыль 18000 была разбита на издержки, равные 0. И Power BI заместо данной нам ошибки вывела значение «Бесконечность».
Для того, чтоб поправить эту ситуацию, в формуле расчета ROI заместо обыденного деления необходимо применять рассматриваемую DAX функцию DIVIDE. Она дозволит нам произвести деление и обработать все ошибки, возникающие при делении на о. И заместо значения «Бесконечность» вывести то значение, которое нам необходимо, к примеру, пустое значение BLANK ().
В итоге, формула расчета ROI на базе функции DIVIDE будет таковая:
Где, в первом параметре функции DIVIDE мы указали сумму прибыли, которую необходимо поделить, во 2-м параметре — сумму издержек, на которую делится сумма прибыли. 3-ий параметр указывать не стали, потому что по дефлоту он равен функции BLANK (), что нам и необходимо.
В итоге, визуализация в Power BI сейчас работает верно:
Используйте функцию деления DIVIDE постоянно, когда имеется хоть мельчайший потенциал значения нуля в делителе Вашей формулы.
DAX функция QUOTIENT в Power BI и Power Pivot
QUOTIENT () — делает деление чисел, входящих в характеристики функции и возвращает целочисленную часть от деления.
Пример формулы на базе DAX функции QUOTIENT.
В Power BI имеется начальная таблица «Общая Продолжительность Звонков», содержащая внутри себя информацию по общей сумме секунд всех дискуссий менеджеров:
Требуется высчитать это количество в целых часах.
Для этого, полное количество секунд необходимо поделить на количество секунд в часе (3600). Но, в итоге этого деления получится дробное число, а нам нужна лишь целая часть результата деления. В данной нам ситуации нам поможет функция QUOTIENT.
В итоге, формула расчета общей продолжительности звонков в целых часах будет таковой:
И в отчете Power BI по любому менеджеру эта мера выведет количество целых часов, которые затратили менеджеры на звонки:
DAX функция MOD в Power BI и Power Pivot
MOD () — возвращает остаток от деления со знаком делителя.
В качестве разбора формулы на базе DAX функции MOD продолжим разглядывать прошедший пример с расчетом продолжительности разговора менеджеров по телефону в целых часах на базе общей суммы в секундах.
Разделив полное количество секунд на 3600 с помощью QUOTIENT, мы получили целую часть от деления. Но, также, при всем этом делении мы можем получить и остаток от этого целочисленного деления (в нашем случае, это оставшееся количество секунд за вычетом целых часов из полного количества секунд).
И создать это можно функцией MOD:
Давайте проверим эту формулу в Power BI:
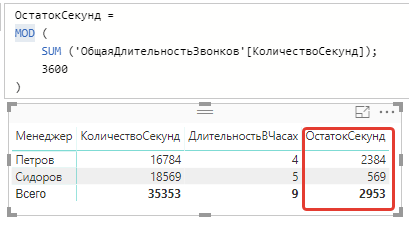
Вправду, если мы разглядим менеджера Петров из визуализации выше, то 16784 (полное количество секунд) — 14400 секунд (4 часа * 3600) = 2384 (остаток секунд). И функция MOD нам также вывела данное значение 2384.
Сейчас, это получившееся значение (остаток секунд) можно снова поделить функцией QUOTIENT на 60 и мы получим целое количество минут из этого остатка секунд:
В Power BI вычисление данной нам формулы будет таковым:
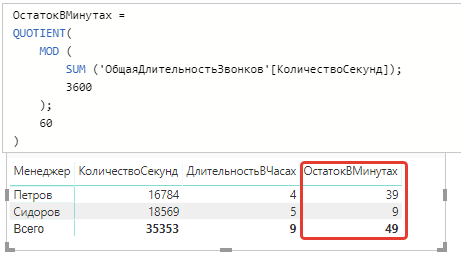
Давайте проверим все вычисления на примере менеджера Петрова: полное количество секунд у него 16784, а 4 часа и 39 минут, это 16740 секунд (60*(4*60+39). Все верно 16740 заходит в полное количество секунд 16784.
Сейчас, осталось вычислить окончательный остаток в секундах:
И в Power BI все это будет смотреться так:
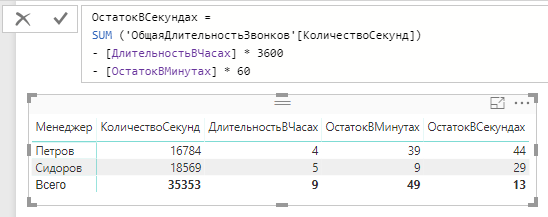
В итоге, осталось навести некоторый «косметический дизайн» — совместим часы, минутки и секунды в единое значение «часы : минутки : секунды», для этого, воспользуемся оператором объединения в языке DAX — & и текстом с двоеточием («:»):
Итоговая визуализация, демонстрирующая совместную работу DAX функций QUOTIENT и MOD в Power BI будет таковая:
Таковым образом, полное количество секунд, затраченное менеджером на звонки мы превратили в соответственное отображение в часах, минутках и секундах.
Давайте проверим все вычисления, так сказать, на калькуляторе, на примере менеджера Сидоров:
Продолжительность звонков = 5:9:29, другими словами — 5 часов, 9 минут и 29 секунд, что равно 18569 секунд (5*3600+9*60+29). А это, в свою очередь, равно начальной сумме секунд по менеджеру Сидоров (18569 секунд).
На этом, с разбором DAX функций DIVIDE (деление на ноль «0»), QUOTIENT (целочисленное деление) и MOD (остаток от целочисленного деления) в Power BI и Power Pivot, все.
Пожалуйста, оцените статью:
- 5
- 4
- 3
- 2
- 1
![[Экспресс-видеокурс] Быстрый старт в языке DAX](https://biprosto.ru/wp-content/uploads/2018/08/kurs-free-5.png)
 Фурроров Для вас, друзья!
Фурроров Для вас, друзья!
С почтением, Будуев Антон.
Проект «BI — это просто»
Если у Вас возникли какие-то вопросцы по материалу данной статьи, задавайте их в комментах ниже. Я Для вас непременно отвечу. Ну и совершенно, просто оставляйте там Вашу оборотную связь, я буду весьма рад.
Также, делитесь данной статьей со своими знакомыми в соц сетях, может быть, этот материал кому-то будет весьма полезен.
Приглянулся материал статьи?
Добавьте эту статью в закладки Вашего браузера, чтоб возвратиться к ней снова. Для этого, прямо на данный момент нажмите на клавиатуре комбинацию кнопок Ctrl+D
Что еще поглядеть / почитать?

Функции подсчета количества в DAX: COUNT, COUNTA, COUNTX, COUNTAX, COUNTBLANK, DISTINCTCOUNT и COUNTROWS (для Power BI и Power Pivot)

Функции объединения таблиц в одну на базе внутренних связей DAX: NATURALINNERJOIN и NATURALLEFTOUTERJOIN в Power BI и Power Pivot
NEXTYEAR, NEXTQUARTER, NEXTMONTH, NEXTDAY — DAX функции, возвращающие даты последующего года, квартала, месяца и денька в Power BI и Power Pivot
Деление чисел с фиксированной запятой в прямом и доп кодах
Деление чисел с фиксированной запятой имеет ряд особенностей по сопоставлению с умножением. Основная из их состоит в том, что личное определяется по одному уровню за любой цикл вычисления, а полное количество разрядов личного и, как следует, циклов вычислений определяется, обычно, нужной точностью, которая зависит как от точности начальных данных, так и от используемых форматов чисел в определенной ЭВМ (Электронная вычислительная машина — комплекс технических средств, предназначенных для автоматической обработки информации в процессе решения вычислительных и информационных задач).
В более всераспространенных в истинное время ЭВМ (Электронная вычислительная машина — комплекс технических средств, предназначенных для автоматической обработки информации в процессе решения вычислительных и информационных задач) с системой установок X86 либо IA-32 деление делается над числами с фиксированной точкой со знаком либо без знака форматом б либо слово. При всем этом итог выходит в виде целой части и остатка, при этом любая часть результата занимает фиксированное число б.
Разумеется, что таковой подход не быть может применен при делении чисел с фиксированной запятой, потому что он подразумевает, что, в общем случае, личное имеет целую часть, огромную нуля, а это противоречит определению формата числа с фиксированной запятой. Для чисел, данных в таком формате, будем исходить из последующих общих критерий, не связанных со структурой определенной ЭВМ (Электронная вычислительная машина — комплекс технических средств, предназначенных для автоматической обработки информации в процессе решения вычислительных и информационных задач):
- делимое и делитель имеют равную длину в n разрядов (для чисел, данных в прямом коде, эти разряды предусмотрены только для хранения модуля числа);
- в случае, если делимое по абсолютной величине больше делителя, итог фиксируется как ±∞, где символ бесконечности определяется из соотношения символов операндов;
- если делимое по абсолютной величине меньше делителя, то итог выходит так же n-разрядным, как и операнды; при всем этом проводится вычисление n+1 разряда результата с следующим округлением до n разрядов.
Эти положения разрешают адаптировать предлагаемые методы деления к ЭВМ (Электронная вычислительная машина — комплекс технических средств, предназначенных для автоматической обработки информации в процессе решения вычислительных и информационных задач) с случайной архитектурой, в том числе, длине слова.
Деление чисел, данных в прямом коде
Разглядим варианты деления чисел для варианта, когда делимое и делитель представлены в прямом коде. При любом методе деления в прямом коде чисел с фиксированной запятой итог, в общем случае, выходит
При любом методе деления в прямом коде чисел с фиксированной запятой итог, формируется поразрядно и так же, как и операнды, в прямом коде. Из этого следует, что в общем случае он формируется «с недочетом», потому что какая-то предстоящая цифра опосля прекращения выполнения операции может оказаться равной единице, тем увеличивая приобретенный итог. Это свойство быть может применено для текущей проверки получаемых в процессе вычислений значений.
Деление со сдвигом и автоматическим восстановлением остатка
На первом шаге проводится определение знака личного:

Потом сравниваем абсолютные величины делимого и делителя.
Если α0 ≥ 0, то |X| ≥ |Y|. Как следует, для чисел с фиксированной запятой Z = ∞, и предстоящее деление не имеет смысла.
Если α0 < 0, то очередные остатки при делении получаем по последующей рекуррентной формуле
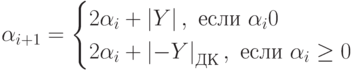 |
Очередные разряды мантиссы результата, начиная с z1, рассчитываются по формуле
 |
Разряды результата получаются в прямом коде.
Тут, как и в остальных рассматриваемых методах деления, при получении еще одного остатка складываются числа различных символов. Это приводит к тому, что переполнения на этом шаге деления никогда не возникает. Потому для выполнения данной операции измененный код не требуется.
Таковым образом, выполнение деления согласно данному методу востребует 2-ух n-разрядных регистров для хранения модулей операндов, 1-го n разрядного регистра для хранения получаемых остатков, триггеров для хранения символов операндов и результата и некого количества комбинационных схем для выполнения операции округления. При этом регистры модулей делимого и делителя могут быть довольно ординарными и владеть лишь функцией параллельной загрузки, а регистр, в каком на любом шаге выходит остаток, обязан иметь также функцию сдвига в сторону старших разрядов.
Пример 9.1
Выполнить деление 2-ух чисел с фиксированной запятой, данных в прямом коде, по методу деления со сдвигом и автоматическим восстановлением остатка: Xпк = 1.0110; Yпк = 0.1010
Решение
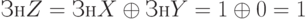
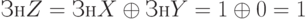


Получив достаточное количество цифр в мантиссе, запишем окончательный итог:


Пример 9.2
Выполнить деление 2-ух чисел с фиксированной запятой, данных в прямом коде, по методу деления со сдвигом и автоматическим восстановлением остатка: Xпк = 0.1110; Yпк = 1.1010.
Решение
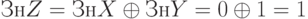


Деление со сдвигом делителя и автоматическим восстановлением остатка
Анализ формул (9.1) и (9.2) указывает, что значение еще одного разряда личного зависит от соотношения двойного значения остатка, приобретенного на прошлом шаге, и модуля делителя.
Метод деления со сдвигом делителя и автоматическим восстановлением остатка базируется на определении этого же соотношения, но заместо удвоения предшествующего остатка он употребляет уменьшение делителя на любом шаге вдвое. В то же время вид формул сохраняется:
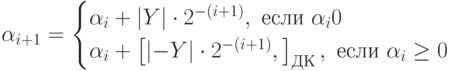 ![alpha_<i+1></noscript>=begin<cases>alpha_i+left| Y right|cdot 2^<-(i+1)>, text < если >alpha_ilt0alpha_i+left[left| -Y right|cdot 2^<-(i+1)>,right]_<ДК>, text < если >alpha_igeq0end<cases>» /></td>
<td valign=](https://intuit.ru/sites/default/files/tex_cache/5d231144b6b59e0a9d795b1289975b0e.png) ( 9.3) ( 9.3) |
   ( 9.4) ( 9.4) |
Анализируя формулу (9.3), можно прийти к выводу, что схемотехнически реализация этого метода востребует n-разрядного регистра для хранения модуля делимого, 2n-разрядного регистра для модуля делителя с учетом его сдвига в сторону младших разрядов, 2n-разрядного регистра для хранения остатка, комбинационные схемы для выполнения операции округления модуля личного, также триггеры для хранения символов операндов и результата.
Как и при выполнении операции умножения, деление без утраты точности можно проводить в укороченной разрядной сетке длиной n+d разрядов, где d = log2n и, соответственно, применять регистры наименьшей разрядности. Плюсы и недочеты такового подхода рассматривались при обсуждении алгоритмов умножения в предшествующей главе. В примерах мы будем применять 2n-разрядную сетку.
Пример 9.3
Выполнить деление 2-ух чисел с фиксированной запятой, данных в прямом коде, по методу деления со сдвигом делителя и автоматическим восстановлением остатка: Xпк = 0.1110; Yпк = 1.1010.
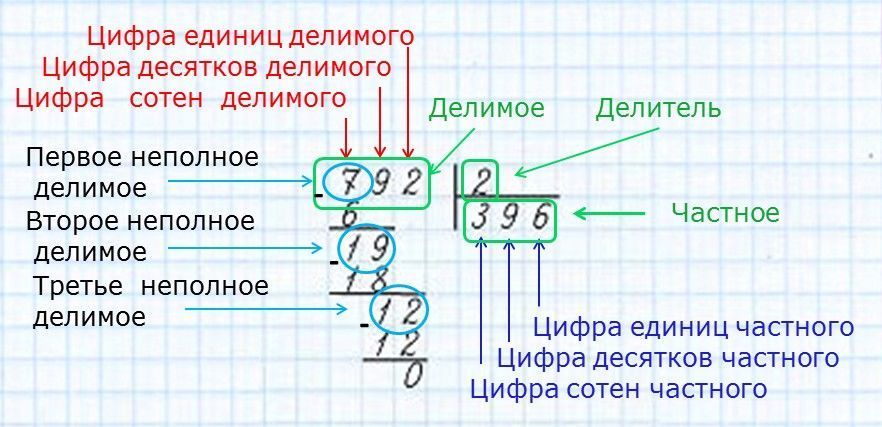
Деление

Деление – одна из 4 главных математических операций (сложение, вычитание, умножение). Деление, как и другие операции принципиально не только лишь в арифметике, да и в ежедневной жизни. К примеру, вы целым классом (человек 25) сдадите средства и купите подарок учительнице, а потратите не все, остается сдача. Итак вот сдачу для вас нужно будет поделить на всех. В работу вступает операция деления, которая поможет для вас решить эту задачку.
Деление – увлекательная операция, в чем мы и убедимся с вами в данной нам статье!


Деление чисел
Итак, незначительно теории, а потом практика! Что такое деление? Деление – это разбивание на равные части чего-либо. Другими словами это быть может пакет конфет, который необходимо разбить на равные части. К примеру, в пакетике 9 конфет, а человек которые желают их получить – три. Тогда необходимо поделить эти 9 конфет на 3-х человек.
Записывается это так: 9:3, ответом будет цифра 3. Другими словами деление числа 9 на число 3 указывает количество чисел три содержащихся в числе 9. Оборотным действием, проверочным, будет умножение. 3*3=9. Правильно? Полностью.
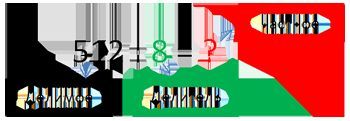
Итак, разглядим пример 12:6. Для начала обозначим имена любому компоненту примера. 12 – делимое, другими словами. число которое делиться на части. 6 – делитель, это число частей, на которое делится делимое. А результатом будет число, имеющее заглавие «личное».
Поделим 12 на 6, ответом будет число 2. Проверить решение можно умножением: 2*6=12. Выходит, что число 6 содержится 2 раза в числе 12.
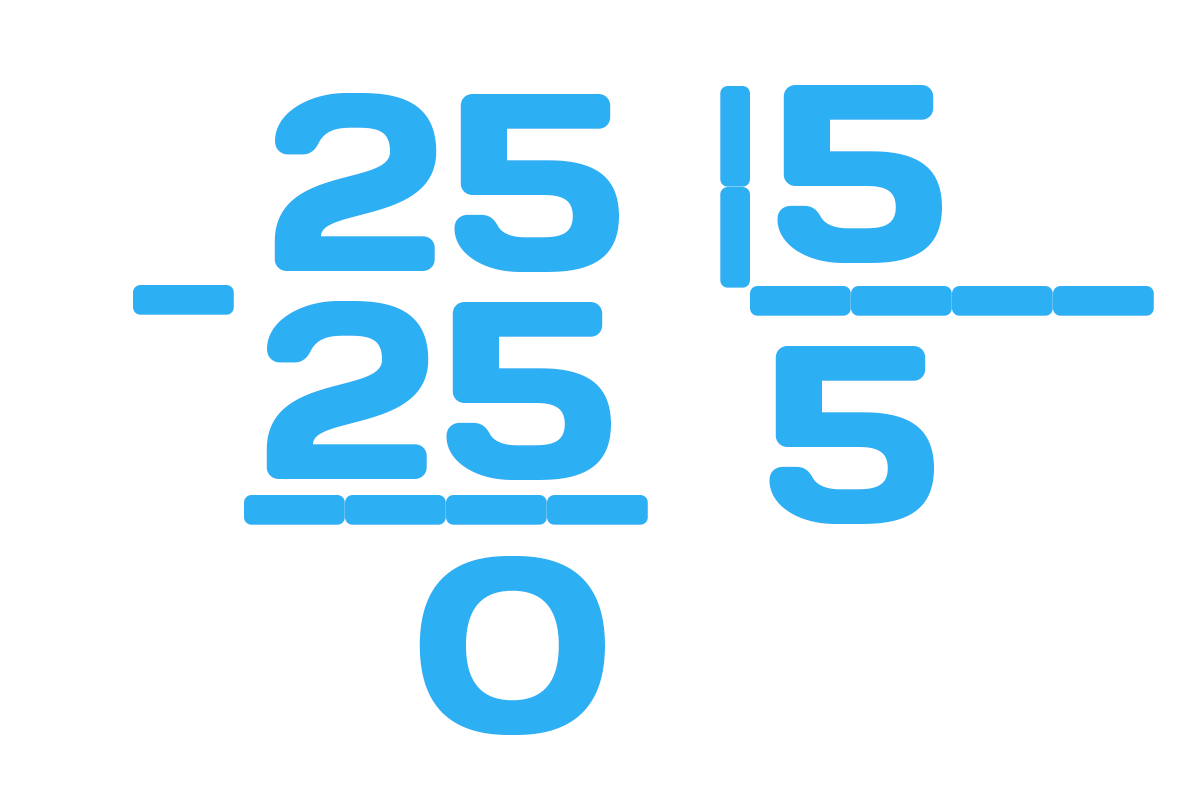
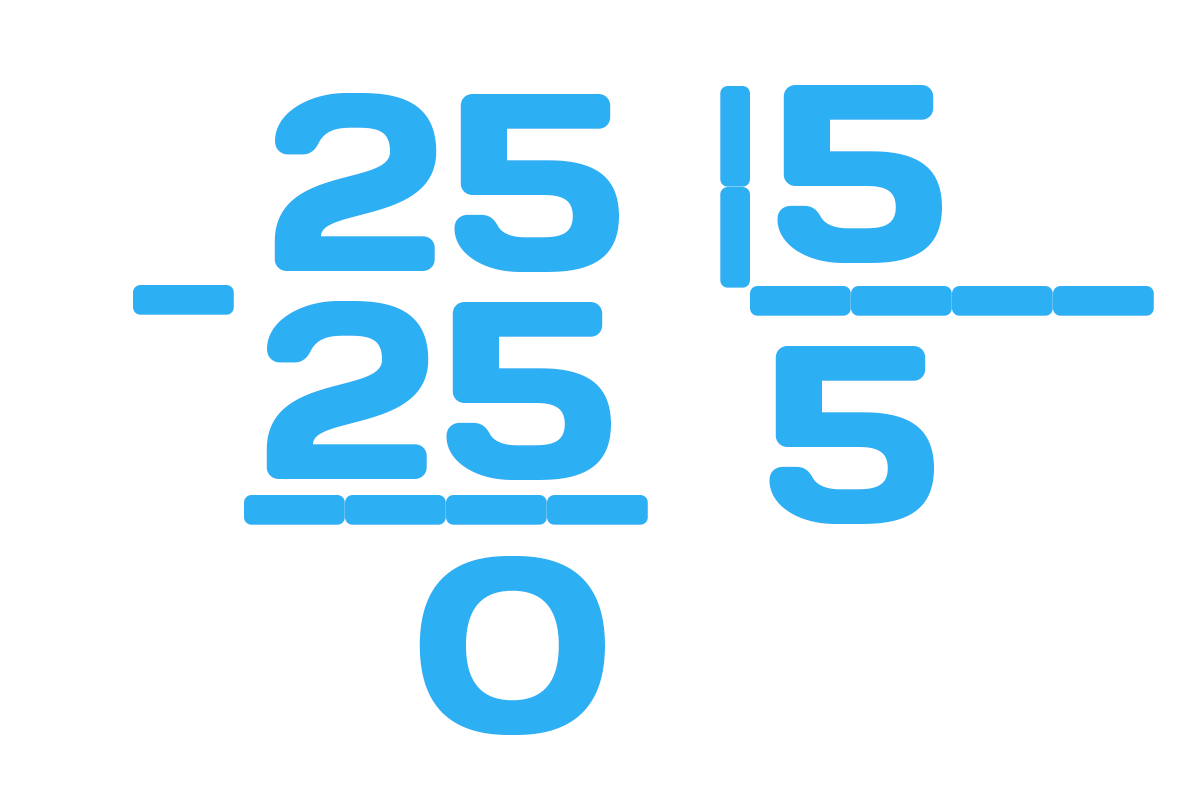
Деление с остатком
Что все-таки такое деление с остатком? Это то же самое деление, лишь в итоге выходит не ровненькое число, как показано выше.
К примеру, поделим 17 на 5. Потому что, наибольшее число, делящееся на 5 до 17 это 15, то ответом будет 3 и остаток 2, а записывается так: 17_5=3(2).
К примеру, 22:7. Буквально так же определяемся очень число, делящееся на 7 до 22. Это число 21. Ответом тогда будет: 3 и остаток 1. А записывается: 22_7=3(1).
Деление на 3 и 9
Личным случаем деления будет деление на число 3 и число 9. Если вы желаете выяснить, делиться ли число на 3 либо 9 без остатка, то для вас будет нужно:
Отыскать сумму цифр делимого.
Поделить на 3 либо 9 (зависимо от того, что для вас необходимо).
Если ответ выходит без остатка, то и число поделится без остатка.
К примеру, число 18. Сумма цифр 1+8 = 9. Сумма цифр делится как на 3, так и на 9. Число 18_9=2, 18_3=6. Поделено без остатка.
К примеру, число 63. Сумма цифр 6+3 = 9. Делится как на 9, так и на 3. 63_9=7, а 63_3=21.Такие операции проводятся с хоть каким числом, чтоб выяснить делится ли оно с остатком на 3 либо 9, либо нет.
Умножение и деление
Умножение и деление – это обратные друг дружке операции. Умножение можно применять как проверку деления, а деление – как проверку умножения. Подробнее выяснить о умножении и освоить операцию сможете в нашей статье про умножение. В какой тщательно описано умножение и как верно делать. Там же отыщите таблицу умножения и примеры для тренировки.
Приведем пример проверки деления и умножения. Допустим, дан пример 6*4. Ответ: 24. Тогда проверим ответ делением: 24_4=6, 24_6=4. Принято решение правильно. В этом случае проверка делается методом деления ответа на один из множителей.
Либо дан пример на деление 56:8. Ответ: 7. Тогда проверкой будет 8*7=56. Правильно? Да. В этом случае проверка делается методом умножения ответа на делитель.
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная математика», чтоб научиться стремительно и верно ложить, вычитать, множить, разделять, возводить числа в квадрат и даже извлекать корешки. За 30 дней вы научитесь применять легкие приемы для упрощения арифметических операций. В любом уроке новейшие приемы, понятные примеры и полезные задания.


Деление 3 класс
В 3-ем классе лишь начинают проходить деление. Потому третьеклассники решают самые обыкновенные задачи:
Задачка 1. Работнику на фабрике дали задание разложить 56 пирожных в 8 упаковок. Сколько пирожных необходимо положить в каждую упаковку, чтоб вышло равно количество в каждой?
Задачка 2. На кануне новейшего года в школе детям на класс, в каком обучается 15 человек, выдали 75 конфет. Сколько конфет должен получить любой ребенок?
Задачка 3. Рома, Саша и Миша собрали с яблони 27 яблок. Сколько любой получит яблок, если необходимо поделить их идиентично?
Задачка 4. Четыре друга приобрели 58 штук печенья. Но позже сообразили, что им не поделить их поровну. Сколько ребятам необходимо докупить печенья, чтоб любой получил по 15 штук?
Деление 4 класс
Деление в четвертом классе – наиболее суровое, чем в 3-ем. Все вычисления проводятся способом деления в столбик, а числа, которые участвуют в делении – не мелкие. Что все-таки такое деление в столбик? Ответ сможете отыскать ниже:
Деление в столбик
Что такое деление в столбик? Это способ позволяющий отыскивать ответ на деление огромных чисел. Если обыкновенные числа как 16 и 4, можно поделить, и ответ понятен – 4. То 512:8 в уме для малыша не попросту. А поведать о технике решения схожих примеров – наша задачка.
Разглядим пример, 512:8.

1 шаг. Запишем делимое и делитель последующим образом:
Личное будет записано в итоге под делителем, а расчеты под делимым.
2 шаг. Деление начинаем слева вправо. Поначалу берем цифру 5:

3 шаг. Цифра 5 меньше числа 8, а означает поделить не получится. Потому берем еще одну цифру делимого:


Сейчас 51 больше 8. Это неполное личное.
4 шаг. Ставим точку под делителем.


5 шаг. Опосля 51 стоит еще цифра 2, а означает в ответе будет очередное число, другими словами. личное – двузначное число. Ставимвторую точку:
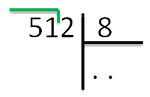
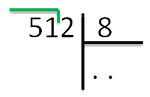
6 шаг. Начинаем операцию деления. Наибольшее число, делимое без остатка на 8 до 51 – 48. Поделив 48 на 8,получаем 6. Записываем число 6 заместо первой точки под делителем:


7 шаг. Потом записываем число ровно под числом 51 и ставим символ «-»:
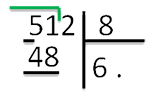
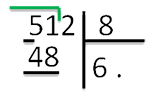
8 шаг. Потом из 51 вычитаем 48 и получаем ответ 3.
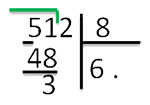
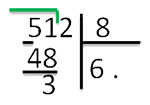
* 9 шаг*. Сносим цифру 2 и записываем рядом с цифрой 3:
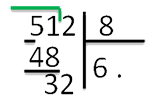
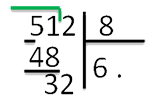
10 шаг Получившееся число 32 делим на 8 и получаем вторую цифру ответа – 4.
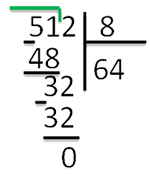

Итак, ответ 64, без остатка. Если б разделяли число 513, то в остатке была бы единица.
Деление трехзначных
Деление трехзначных чисел производится способом деления в столбик, который был объяснен на примере выше. Пример как раз-таки трехзначного числа.
Деление дробей
Деление дробей не так трудно, как кажется на 1-ый взор. К примеру, (2/3):(1/4). Способ такового деления достаточно прост. 2/3 – делимое, 1/4 – делитель. Можно поменять символ деления (:) на умножение (), но для этого необходимо поменять местами числитель и знаменатель делителя. Другими словами получаем: (2/3)(4/1), (2/3)*4, это равно – 8/3 либо 2 целые и 2/3.Приведем еще пример, с иллюстрацией для лучшего осознания. Разглядим дроби (4/7):(2/5):
Как и в прошлом примере, переворачиваем делитель 2/5 и получаем 5/2, заменяя деление на умножение. Получаем тогда (4/7)*(5/2). Производим сокращение и ответ:10/7, потом выносим целую часть: 1 целая и 3/7.
Деление числа на классы
Представим число 148951784296, и поделим его по три числа: 148 951 784 296. Итак, справа влево: 296 – класс единиц, 784 — класс тыщ, 951 – класс миллионов, 148 – класс млрд. В свою очередь, в любом классе 3 числа имеют собственный разряд. Справа влево: 1-ая цифра – единицы, 2-ая цифра – 10-ки, 3-я – сотки. К примеру, класс единиц – 296, 6 – единицы, 9 – 10-ки, 2 – сотки.


Деление натуральных чисел


Деление натуральных чисел – это самое обычное деление описанные в данной статье. Оно быть может, как с остатком, так и без остатка. Делителем и делимым могут быть любые не дробные, целые числа.
Запишитесь на курс «Ускоряем устный счет, НЕ ментальная математика», чтоб научиться стремительно и верно ложить, вычитать, множить, разделять, возводить числа в квадрат и даже извлекать корешки. За 30 дней вы научитесь применять легкие приемы для упрощения арифметических операций. В любом уроке новейшие приемы, понятные примеры и полезные задания.
Деление презентация
Презентация – очередной метод наглядно показать тему деления. Ниже мы отыщите ссылку на красивую презентацию, в какой отлично разъясняется как разделять, что такое деление, что такое делимое, делитель и личное. Время напрасно не потратите, а свои познания закрепите!









