Эконометрика. Линейная Регрессия в MS Excel

На мой взор, как студента, эконометрика – это одна из самых прикладных наук из всех, с которыми мне удалось познакомиться в стенках собственного института. При помощи неё, вправду, можно решать задачки прикладного нрава в масштабах компании. Как действенными будут эти решения – вопросец 3-ий. Сущность в том, что большая часть познаний так и остается теорией, а вот эконометрика и регрессионный анализ всё-таки стоит изучить с особенным вниманием.

Что разъясняет регрессия?

До этого, чем мы приступим к рассмотрению функций MS Excel, позволяющих, решать данные задачки, хотелось бы для вас на пальцах разъяснить, что, в сути, подразумевает регрессионный анализ. Так для вас проще будет сдавать экзамен, а самое основное, интересней учить предмет.

Будем надежды, вы знакомы с понятием функции из арифметики. Функция – это связь 2-ух переменных. При изменении одной переменной что-то происходит с иной. Изменяем X, изменяется и Y, соответственно. Функциями описываются разные законы. Зная функцию, мы можем подставлять произвольные значения X и глядеть на то, как при всем этом поменяется Y.

Это имеет огромное значение, так как регрессия – это попытка разъяснить при помощи определённой функции на 1-ый взор бессистемные и беспорядочные процессы. Так, к примеру, можно выявить связь курса бакса и безработицы в Рф.

Если данную закономерность найти получится, то по приобретенной нами в процессе расчетов функции, мы сможем составить прогноз, какой будет уровень безработицы при N-ом курсе бакса по отношению к рублю.
Данная связь будет называться корреляцией. Регрессионный анализ подразумевает расчет коэффициента корреляции, который растолкует тесноту связи меж рассматриваемыми нами переменными (курсом бакса и числом рабочих мест).

Данный коэффициент быть может положительным и отрицательным. Его значения находятся в границах от -1 до 1. Соответственно, мы может следить высшую отрицательную либо положительную корреляцию. Если она положительная, то за повышением курса бакса последует и возникновение новейших рабочих мест. Если она отрицательная, означает, за повышением курса, последует уменьшение рабочих мест.

Регрессия бывает нескольких видов. Она быть может линейной, параболической, степенной, экспоненциальной и т.д. Выбор модели мы делаем зависимо от того, какая регрессия будет соответствовать непосредственно нашему случаю, какая модель будет очень близка к нашей корреляции. Разглядим это на примере задачки и решим её в MS Excel.

Линейная регрессия в MS Excel

Для решения задач линейной регрессии для вас пригодится функционал «Анализ данных». Он быть может не включен у вас потому его необходимо активировать.

• Жмём на клавишу «Файл»;
• Избираем пункт «Характеристики»;
• Жмём по предпоследней вкладке «Надстройки» с левой стороны;

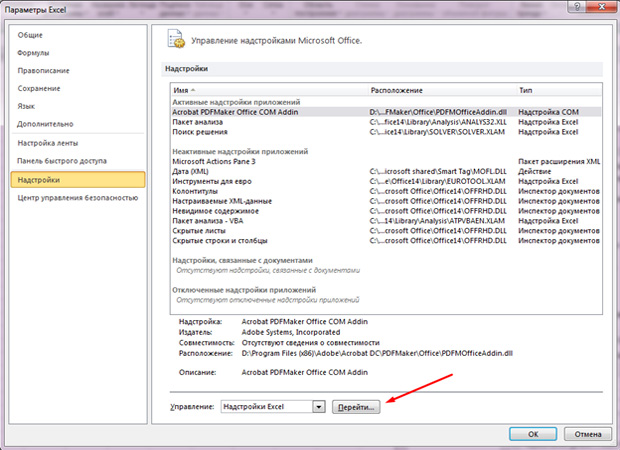
• Снизу увидим Надпись «Управление» и клавишу «Перейти». Жмём по ней;
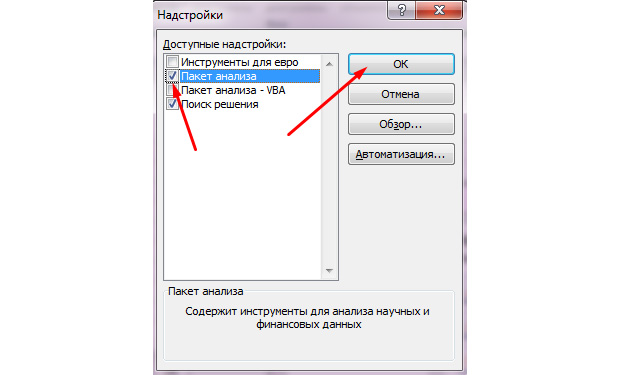
• Ставим галочку на «Пакет анализа»;
• Жмём «ок».

Пример задачки

Функция пакетного анализа активирована. Решим последующую задачку. У нас есть подборка данных за пару лет о числе ЧП на местности компании и количестве трудоустроенных работников. Нам нужно выявить связь меж этими 2-мя переменными. Есть объясняющая переменная X – это число рабочих и объясняемая переменная – Y – это число чрезвычайных происшествий. Распределим начальные данные в два столбца.

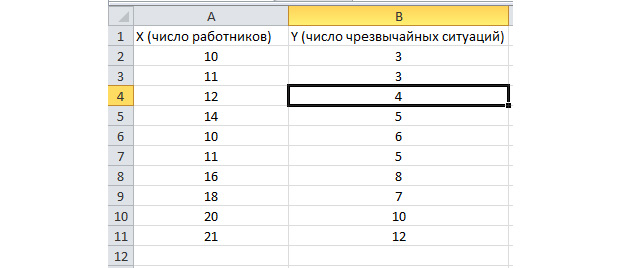
Перейдём во вкладку «данные» и выберем «Анализ данных»

В показавшемся перечне избираем «Регрессия». Во входных интервалах Y и X избираем надлежащие значения.

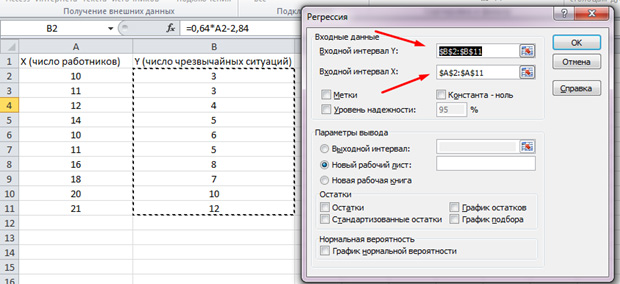
Жмем «Ок». Анализ произведён, и в новеньком листе мы увидим результаты.

Более значительные для нас значения отмечены на рисунке ниже.

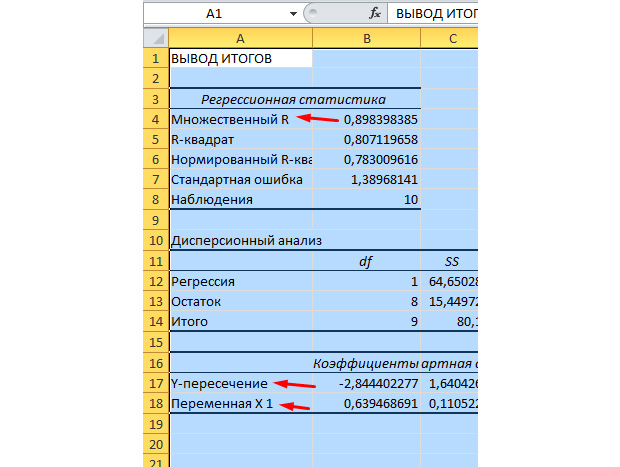
Множественный R – это коэффициент детерминации. Он имеет сложную формулу расчета и указывает, как можно довериться нашему коэффициенту корреляции. Соответственно, чем больше это значение, тем больше доверия, тем удачнее наша модель в целом.

Y-пересечение и Пересечение X1 – это коэффициенты нашей регрессии. Как уже было сказано, регрессия – это функция, и у неё есть определённые коэффициенты. Таковым образом, наша функция будет иметь вид: Y = 0,64*X-2,84.

Что нам это даёт? Это даёт нам возможность составить прогноз. Допустим, мы желаем нанять на предприятие 25 работников и нам необходимо приблизительно представить, каким при всем этом будет количество чрезвычайных происшествий. Подставляем в нашу функцию данное значение и получаем итог Y = 0,64 * 25 – 2,84. Приблизительно 13 ЧП у нас будет происходить.

Поглядим, как это работает. Посмотрите на набросок ниже. В полученную нами функцию подставлены фактические значения по вовлеченным работникам. Поглядите, как близки значения к настоящим игрекам.

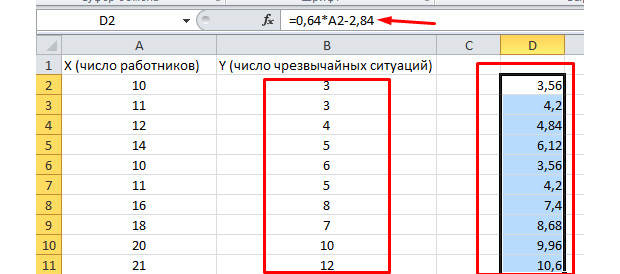
Вы так же сможете выстроить поле корреляции, выделив область игреков и иксов, нажав на вкладку «вставку» и выбрав точечную диаграмму.

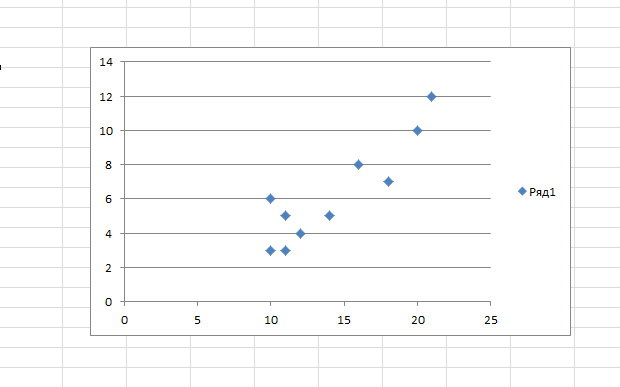
Точки идут вразброс, но в целом двигаются ввысь, как как будто в центре лежит ровная линия. И эту линию вы так же сможете добавить, перейдя во вкладку «Макет» в MS Excel и выбрав пункт «Линия тренда»

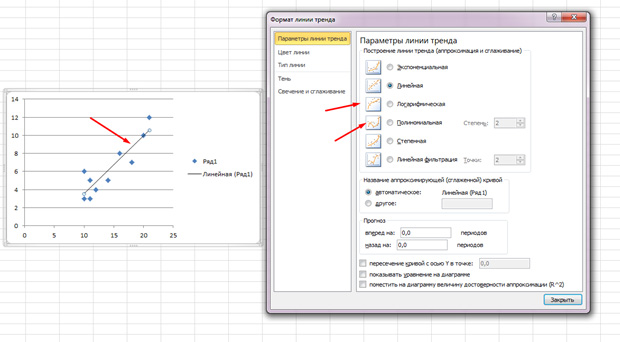
Щелкните два раза по показавшейся полосы и увидите то, о чем говорилось ранее. Вы сможете изменять тип регрессии зависимо от того, как смотрится ваше поле корреляции.

Может быть, для вас покажется, что точки отрисовывают параболу, а не прямую линию и для вас целесообразней избрать иной тип регрессии.

Заключение

Будем надежды, что данная статья отдала для вас большее осознание о том, что такое регрессионный анализ и для что он нужен. Всё это имеет огромное прикладное значение.

Аппроксимация в Excel

(Направьте внимание на доп раздел от 04.06.2017 в конце статьи.)

Учет и контроль! Те, кому за 40 должны отлично держать в голове этот девиз из эры построения социализма и коммунизма в нашей стране.

Но без отлично налаженного учета нереально действенное функционирование ни страны, ни области, ни компании, ни домашнего хозяйства при хоть какой общественно-экономической формации общества! Для составления прогнозов и планов деятельности и развития нужны начальные данные. Где их брать? Лишь один достоверный источник – это ваши статистические учетные данные прошлых периодов времени.

Учесть результаты собственной деятельности, собирать и записывать информацию, обрабатывать и рассматривать данные, использовать результаты анализа для принятия правильных решений в дальнейшем должен, в моем осознании, любой адекватномыслящий человек. Это есть ничто другое, как скопление и рациональное внедрение собственного актуального опыта. Если не вести учет принципиальных данных, то вы через определенный период времени их забудете и, начав заниматься этими вопросцами вновь, вы снова наделаете те же ошибки, что делали, когда в первый раз сиим занимались.

«Мы, помню, 5 годов назад изготавливали до 1000 штук таковых изделий за месяц, а на данный момент и 700 еле-еле собираем!». Открываем статистику и лицезреем, что 5 годов назад и 500 штук не изготавливали…

«Во сколько обходится километр пробега твоего кара с учетом всех издержек?» Открываем статистику – 6 руб./км. Поездка на работу – 107 рублей. Дешевле, чем на такси (180 рублей) наиболее чем в полтора раза. А бывали времена, когда на такси было дешевле…

«Сколько времени требуется для производства металлоконструкций уголковой башни связи высотой 50 м?» Открываем статистику – и через 5 минут готов ответ…

«Сколько будет стоить ремонт комнаты в квартире?» Поднимаем старенькые записи, делаем поправку на инфляцию за прошедшие годы, учитываем, что в прошедший раз приобрели материалы на 10% дешевле рыночной цены и – приблизительную стоимость мы уже знаем…

Ведя учет собственной проф деятельности, вы постоянно будете готовы ответить на вопросец начальника: «Когда. ». Ведя учет домашнего хозяйства, легче спланировать расходы на большие покупки, отдых и остальные расходы в дальнейшем, приняв надлежащие меры по доп заработку либо по сокращению необязательных расходов сейчас.

В данной статье я на ординарном примере покажу, как можно обрабатывать собранные статистические данные в Excel для способности предстоящего использования при прогнозировании будущих периодов.

Аппроксимация в Excel статистических данных аналитической функцией.

Производственный участок делает строй металлоконструкции из листового и профильного металлопроката. Участок работает размеренно, заказы однотипные, численность рабочих колеблется некординально. Есть данные о выпуске продукции за прошлые 12 месяцев и о количестве переработанного в эти периоды времени металлопроката по группам: листы, двутавры, швеллеры, уголки, трубы круглые, профили прямоугольного сечения, круглый прокат. Опосля подготовительного анализа начальных данных появилось предположение, что суммарный месячный выпуск металлоконструкций значительно зависит от количества уголков в заказах. Проверим это предположение.

До этого всего, несколько слов о аппроксимации. Мы будем находить закон – аналитическую функцию, другими словами функцию, заданную уравнением, которое лучше остальных обрисовывает зависимость общего выпуска металлоконструкций от количества уголкового проката в выполненных заказах. Это и есть аппроксимация, а отысканное уравнение именуется аппроксимирующей функцией для начальной функции, данной в виде таблицы.

1. Включаем Excel и помещаем на лист таблицу с данными статистики.

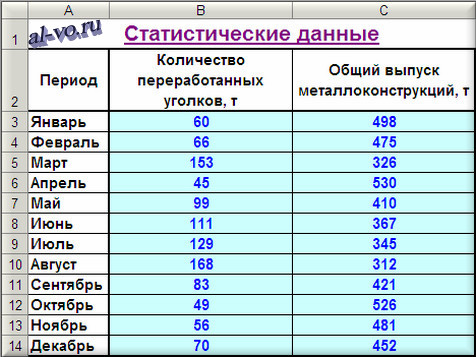
2. Дальше строим и форматируем точечную диаграмму, в какой по оси X задаем значения аргумента – количество переработанных уголков в тоннах. По оси Y откладываем значения начальной функции – общий выпуск металлоконструкций за месяц, данные таблицей.

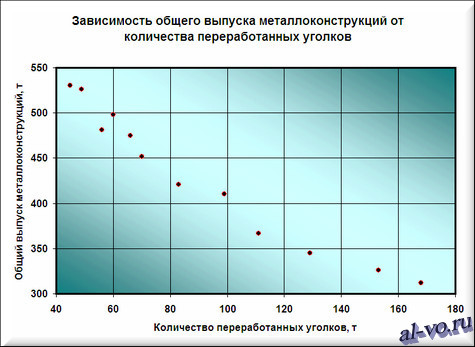
О том, как выстроить схожую диаграмму, тщательно поведано в статье «Как строить графики в Excel?».

3. «Наводим» мышь на всякую из точек на графике и щелчком правой клавиши вызываем контекстное меню (как гласит один мой неплохой товарищ — работая в незнакомой программке, когда не знаешь, что созодать, почаще щелкай правой клавишей мыши…). В выпавшем меню избираем «Добавить линию тренда…».

4. В показавшемся окне «Линия тренда» на вкладке «Тип» избираем «Линейная».

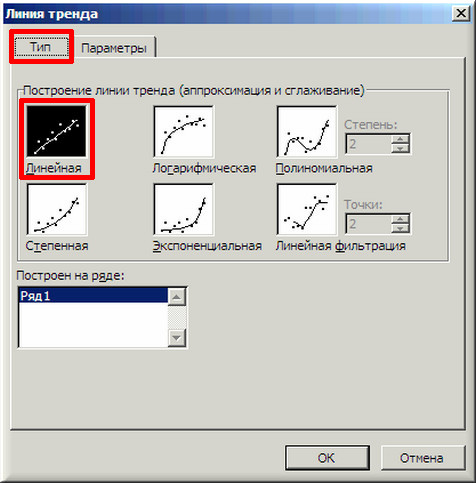
5. Дальше на вкладке «Характеристики» ставим 2 галочки и жмем «ОК».

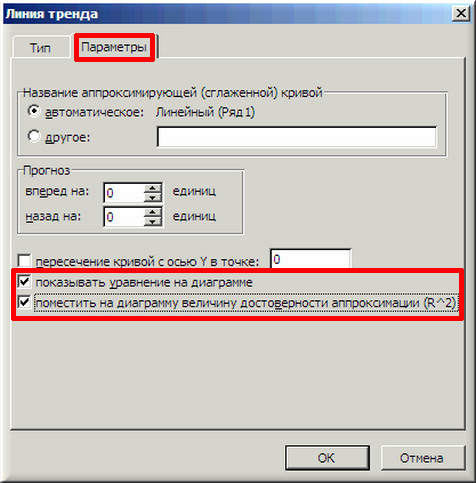
6. На графике возникла ровная линия, аппроксимирующая нашу табличную зависимость.

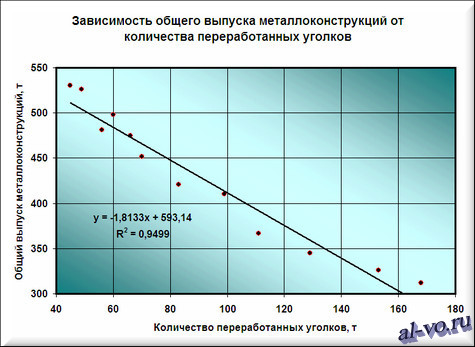
Мы лицезреем не считая самой полосы уравнение данной полосы и, основное, мы лицезреем значение параметра R 2 – величины достоверности аппроксимации! Чем поближе его значение к 1, тем более буквально избранная функция аппроксимирует табличные данные!

7. Строим полосы тренда, используя степенную, логарифмическую, экспоненциальную и полиномиальную аппроксимации по аналогии с тем, как мы строили линейную линию тренда.

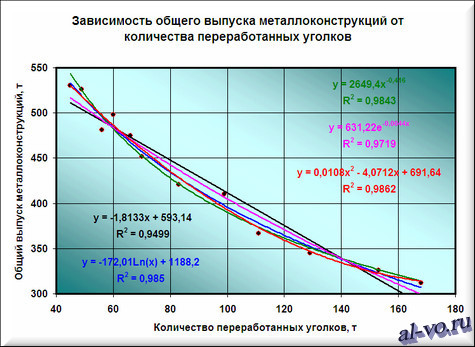
Лучше всех из избранных функций аппроксимирует наши данные полином 2-ой степени, у него наибольший коэффициент достоверности R 2 .

Но желаю вас предостеречь! Если вы возьмете полиномы наиболее больших степеней, то, может быть, получите еще наилучшие результаты, но кривые будут иметь замудренный вид…. Тут принципиально осознавать, что мы отыскиваем функцию, которая имеет физический смысл. Что это значит? Это значит, что нам нужна аппроксимирующая функция, которая будет выдавать адекватные результаты не только лишь снутри рассматриваемого спектра значений X, да и за его пределами, другими словами ответит на вопросец: «Какой будет выпуск металлоконструкций при количестве переработанных в месяц уголков меньше 45 и больше 168 тонн!» Потому я не рекомендую увлекаться полиномами больших степеней, ну и параболу (полином 2-ой степени) выбирать осторожно!

Итак, нам нужно избрать функцию, которая не только лишь отлично интерполирует табличные данные в границах спектра значений X=45…168, да и допускает адекватную экстраполяцию за пределами этого спектра. Я выбираю в этом случае логарифмическую функцию, хотя можно избрать и линейную, как более ординарную. В рассматриваемом примере при выбирании линейной аппроксимации в excel ошибки будут больше, чем при выбирании логарифмической, но не на много.

8. Удаляем все полосы тренда с поля диаграммы, не считая логарифмической функции. Для этого щелкаем правой клавишей мыши по ненадобным линиям и в выпавшем контекстном меню избираем «Очистить».

9. В окончании добавим к точкам табличных данных планки погрешностей. Для этого правой клавишей мыши щелкаем на хоть какой из точек на графике и в контекстном меню избираем «Формат рядов данных…» и настраиваем данные на вкладке «Y-погрешности» так, как на рисунке ниже.

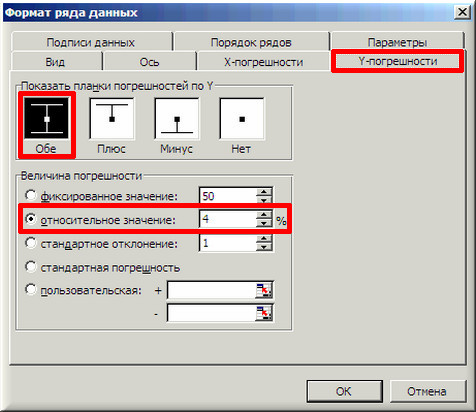
10. Потом щелкаем по хоть какой из линий диапазонов погрешностей правой клавишей мыши, избираем в контекстном меню «Формат полос погрешностей…» и в окне «Формат планок погрешностей» на вкладке «Вид» настраиваем цвет и толщину линий.

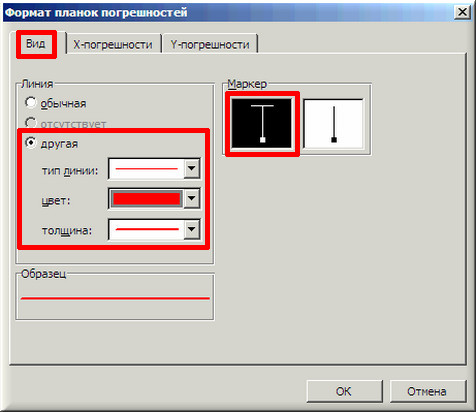
Аналогичным образом форматируются любые остальные объекты диаграммы в Excel!

Окончательный итог диаграммы представлен на последующем скриншоте.

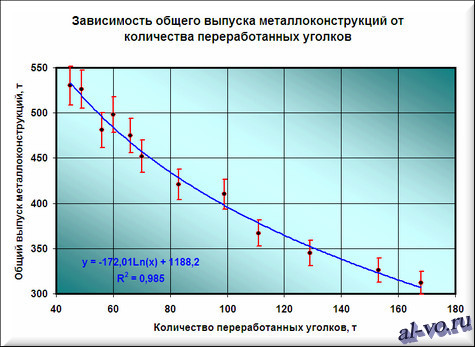
Итоги.

Результатом всех прошлых действий стала приобретенная формула аппроксимирующей функции y=-172,01*ln (x)+1188,2. Зная ее, и количество уголков в месячном наборе работ, можно с высочайшей степенью вероятности (±4% — смотри планки погрешностей) спрогнозировать общий выпуск металлоконструкций в месяц! К примеру, если в плане на месяц 140 тонн уголков, то общий выпуск, быстрее всего, при иных равных составит 338±14 тонн.

Для увеличения достоверности аппроксимации статистических данных обязано быть много. Двенадцать пар значений – это мало.

Из практики скажу, что неплохим результатом следует считать нахождение аппроксимирующей функции с коэффициентом достоверности R 2 >0,87. Хороший итог – при R 2 >0,94.

На практике бывает тяжело выделить один самый основной определяющий фактор (в нашем примере – масса переработанных в месяц уголков), но если попытаться, то в каждой определенной задачке его постоянно можно отыскать! Естественно, общий выпуск продукции в месяц реально зависит от сотки причин, для учета которых нужны значительные трудовые затраты нормировщиков и остальных профессионалов. Лишь итог все равно будет ориентировочным! Так стоит нести издержки, если есть еще наиболее доступное математическое моделирование!

В данной статье я только прикоснулся к вершине айсберга под заглавием сбор, обработка и практическое внедрение статистических данных. О том удалось, либо нет, мне расшевелить ваш энтузиазм к данной теме, надеюсь выяснить из объяснений и рейтинга статьи в поисковиках.

Затронутый вопросец аппроксимации функции одной переменной имеет обширное практическое применение в различных сферах жизни. Но еще большее применение имеет решение задачки аппроксимации функции нескольких независящих переменных…. О этом и не только лишь читайте в последующих статьях на блоге.

Подписывайтесь на новости статей в окне, расположенном в конце каждой статьи либо в окне вверху странички.

Не запамятовывайте подтверждать подписку кликом по ссылке в письме, которое придет к для вас на обозначенную почту (может придти в папку «Мусор»).

С энтузиазмом прочту Ваши комменты, почетаемые читатели! Пишите!

P.S. (04.06.2017)

Высокоточная прекрасная подмена табличных данных обычным уравнением.

Вас не устраивают приобретенные точность аппроксимации (R 2 <0,95) либо вид и набор функций, предлагаемые MS Excel?

Размеры выражения и форма полосы аппроксимирующего полинома высочайшей степени не веселит глаз?

Обращайтесь через страничку «Оборотная связь» для получения наиболее четкого и малогабаритного результата аппроксимации ваших табличных данных и для того, чтоб выяснить ординарную методику решения задач высокоточной аппроксимации функцией одной переменной.

Дальше на снимке экрана в качестве сопоставления представлены поисковые результаты аппроксимирующей функции с помощью Excel и с помощью предлагаемой методики.

При использовании предлагаемого метода действий найдена очень малогабаритная функция, обеспечивающая высочайшую точность аппроксимации: R 2 =0,9963.