Тщательно о генераторах случайных и псевдослучайных чисел

На Хабре и в сети нередко начали появляться статьи, посвященные уязвимостям генераторов случайных чисел. Эта тема очень пространна и является одной из главных в криптографии. Под катом находится описание случайных чисел от A до Z. Статья является результатом вольного перевода цикла статей из 1-го западного блога и личных дополнений создателя. Основная цель — получить feedback и поделиться познаниями.

Введение

Генераторы сессий (PHPSESSID)
Генерация текста для капчи
Шифрование
Генерация соли для хранения паролей в необратимом виде
Генератор паролей
Порядок раздачи карт в веб казино

Как отличить случайную последовательность чисел от неслучайной?

Пусть есть последовательность чисел: 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 . Является ли она случайной? Есть серьезное определение для случайной величины. Случайная величина — это величина, которая воспринимает в итоге опыта одно из огромного количества значений, причём возникновение того либо другого значения данной нам величины до её измерения недозволено буквально предсказать. Но оно не помогает ответить на наш вопросец, потому что нам не хватает инфы для ответа. Сейчас скажем, что данные числа вышли набором одной из верхних строк клавиатуры. «Естественно не случайная» — вскричите Вы и здесь же назовете последующие число и будете полностью правы. Последовательность будет случайной лишь если меж знаками, нету зависимости. К примеру, если б данные знаки возникли в итоге вытягивания бочонков в лото, то последовательность была бы случайной.

Чуток наиболее непростой пример либо число Пи

Последовательность числа в числе Пи считается случайной. Пусть генератор основывается на выводе бит представления числа Пи, начиная с некий неведомой точки. Таковой генератор, может быть и пройдет «тест на последующий бит», потому что ПИ, видимо, является случайной последовательностью. Но этот подход не является критографически надежным — если криптоаналитик обусловит, какой бит числа Пи употребляется на этот момент, он сумеет вычислить и все предыдущие и следующие биты.
Данный пример накладывает ещё одно ограничение на генераторы случайных чисел. Криптоаналитик не обязан иметь способности предсказать работу генератора случайных чисел.

Отличие генератора псевдослучайных чисел (ГПСЧ) от генератора случайных чисел (ГСЧ)

Источники энтропии употребляются для скопления энтропии с следующим получением из неё исходного значения (initial value, seed), нужного генераторам случайных чисел (ГСЧ) для формирования случайных чисел. ГПСЧ употребляет единственное изначальное значение, откуда и следует его псевдослучайность, а ГСЧ постоянно сформировывает случайное число, имея сначала высококачественную случайную величину, предоставленную разными источниками энтропии.
Энтропия – это мера кавардака. Информационная энтропия — мера неопределённости либо непредсказуемости инфы.
Можно сказать, что ГСЧ = ГПСЧ + источник энтропии.

Уязвимости ГПСЧ

Прогнозируемая зависимость меж числами.
Предсказуемое изначальное значение генератора.
Малая длина периода генерируемой последовательности случайных чисел, опосля которой генератор зацикливается.

Линейный конгруэнтный ГПСЧ (LCPRNG)

Распространённый способ для генерации псевдослучайных чисел, не владеющий криптографической стойкостью. Линейный конгруэнтный способ заключается в вычислении членов линейной рекуррентной последовательности по модулю некого натурального числа m, задаваемой последующей формулой:

где a (multiplier), c (addend), m (mask) — некие целочисленные коэффициенты. Получаемая последовательность зависит от выбора стартового числа (seed) X0 и при различных его значениях получаются разные последовательности случайных чисел.

Для выбора коэффициентов имеются характеристики дозволяющие максимизировать длину периода(наибольшая длина равна m), другими словами момент, с которого генератор зациклится [1].

Пусть генератор выдал несколько случайных чисел X0, X1, X2, X3. Выходит система уравнений

Решив эту систему, можно найти коэффициенты a, c, m. Как утверждает википедия [8], эта система имеет решение, но решить без помощи других либо отыскать решение не вышло. Буду весьма благодарен за всякую помощь в этом направлении.

Пророчество результатов линейно-конгруэнтного способа

Главным методом пророчества чисел для линейно-конгруэнтного способа является Plumstead’s — метод, реализацию, которого можно отыскать тут [4](есть онлайн пуск) и тут [5]. Описание метода можно отыскать в [9].
Обычная реализация конгруэнтного способа на Java.

Послав 20 чисел на веб-сайт [4], можно с большенный вероятностью получить последующие. Чем больше чисел, тем больше возможность.

Взлом встроенного генератора случайных чисел в Java

Почти все языки программирования, к примеру C(rand), C++(rand) и Java употребляют LСPRNG. Разглядим, как можно провести взлом на примере java.utils.Random. Зайдя в начальный код (jdk1.7) данного класса можно узреть применяемые константы

Способ java.utils.Randon.nextInt() смотрится последующим образом (тут bits == 32)

Результатом является nextseed сдвинутый на право на 48-32=16 бит. Данный способ именуется truncated-bits, в особенности неприятен при black-box, приходится добавлять ещё один цикл в brute-force. Взлом будет происходить способом грубой силы(brute-force).

Пусть мы знаем два попорядку сгенерированных числа x1 и x2. Тогда нужно перебрать 2^16 = 65536 вариантов oldseed и использовать к x1 формулу:

до того времени, пока она не станет равной x2. Код для brute-force может смотреться так

Нетрудно осознать, что мы отыскали не самый 1-ый seed, а seed, применяемый при генерации второго числа. Для нахождения начального seed нужно провести несколько операций, которые Java употребляла для преобразования seed, в оборотном порядке.

И сейчас в начальном коде заменим
crackingSeed.set(seed);
на
crackingSeed.set(getPreviousSeed(seed));

И всё, мы удачно взломали ГПСЧ в Java.

Взлом ГПСЧ Mersenne twister в PHP

Разглядим ещё один не криптостойкий метод генерации псевдослучайных чисел Mersenne Twister. Главные достоинства метода — это скорость генерации и большой период 2^19937 − 1, Сейчас будем рассматривать реализацию метода mt_srand() и mt_rand() в начальном коде php версии 5.4.6.

Можно увидеть, что php_mt_reload вызывается при инициализации и опосля вызова php_mt_rand 624 раза. Начнем взлом с конца, обратим трансформации в конце функции php_mt_rand(). Разглядим (s1 ^ (s1 >> 18)). В бинарном представление операция смотрится так:

10110111010111100111111001110010 s1
00000000000000000010110111010111100111111001110010 s1 >> 18
10110111010111100101001110100101 s1 ^ (s1 >> 18)
Видно, что 1-ые 18 бит (выделены жирным) остались без конфигураций.
Напишем две функции для инвертирования битового сдвига и xor

Тогда код для инвертирования крайних строк функции php_mt_rand() будет смотреться так

Если у нас есть 624 поочередных числа сгенерированных Mersenne Twister, то применив этот метод для этих поочередных чисел, мы получим полное состояние Mersenne Twister, и сможем просто найти каждое следующее значение, запустив php_mt_reload для известного набора значений.

Область для взлома

Если вы думаете, что уже нечего разламывать, то Вы глубоко заблуждаетесь. Одним из увлекательных направлений является генератор случайных чисел Adobe Flash(Action Script 3.0). Его индивидуальностью является закрытость начального кода и отсутствие задания seed’а. Главный энтузиазм к нему, это внедрение в почти всех онлайн-казино и онлайн-покере.
Есть много последовательностей чисел, начиная от курса бакса и заканчивая количеством времени проведенным в пробке любой денек. И отыскать закономерность в таковых данных весьма не обычная задачка.

Интересно почитать: Как в excel посчитать средневзвешенное значение

Задание распределения для генератора псевдослучайных чисел

Для хоть какой случайной величины можно задать распределение. Перенося на пример с картами, можно создать так, чтоб тузы выпадали почаще, чем девятки. Дальше представлены несколько примеров для треугольного распределения и экспоненциального распределения.

Треугольное распределение

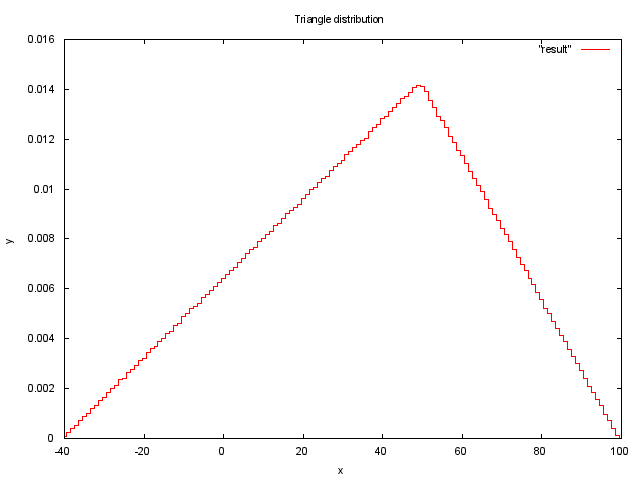
Приведем пример генерации случайной величины с треугольным распределением [7] на языке C99.

В этом случае мы берем случайную величину rand() и задаем ей распределение, исходя из функции треугольного распределения. Для характеристик a = -40, b = 100, c = 50 график 10000000 измерений будет смотреться так

Экспоненциальное распределение

Пусть требуется получить датчик экспоненциально распределенных случайных величин. В этом случае F(x) = 1 – exp(-lambda * x). Тогда из решения уравнения y = 1 – exp(-lambda * x) получаем x = -log(1-y)/lambda.
Можно увидеть, что выражение под знаком логарифма в крайней формуле имеет равномерное распределение на отрезке [0,1), что позволяет получать другую, но так же распределённую последовательность по формуле: x = -log(y)/lambda, где y есть случайная величина(rand()).

Тесты ГПСЧ

Некоторые разработчики считают, что если они скроют используемый ими метод генерации или придумают свой, то этого достаточно для защиты. Это очень распространённое заблуждение. Следует помнить, что есть специальные методы и приемы для поиска зависимостей в последовательности чисел.

Одним из известных тестов является тест на следующий бит — тест, служащий для проверки генераторов псевдослучайных чисел на криптостойкость. Тест гласит, что не должно существовать полиномиального алгоритма, который, зная первые k битов случайной последовательности, сможет предсказать k+1 бит с вероятностью большей ½.

В теории криптографии отдельной проблемой является определение того, насколько последовательность чисел или бит, сгенерированных генератором, является случайной. Как правило, для этой цели используются различные статистические тесты, такие как DIEHARD или NIST. Эндрю Яо в 1982 году доказал, что генератор, прошедший «тест на следующий бит», пройдет и любые другие статистические тесты на случайность, выполнимые за полиномиальное время.
В интернете [10] можно пройти испытания DIEHARD и огромное количество остальных, чтоб найти критостойкость метода.

Случайные числа не случайны

Вы когда-нибудь думали, как работает Math.random()? Что такое случайное число и как оно выходит? А представьте вопросец на собеседовании — напишите собственный генератор случайных чисел в пару строк кода. И так, что все-таки это такое, случайность и может быть ли ее предсказать.

Генератор псевдослучайных чисел и генератор случайных чисел

Для того, чтоб получить что-то случайное, нам нужен источник энтропии, источник некоторого хаоса из который мы будем применять для генерации случайности.

Этот источник употребляется для скопления энтропии с следующим получением из неё исходного значения (initial value, seed), которое нужно генераторам случайных чисел (ГСЧ) для формирования случайных чисел.

Генератор ПсевдоСлучайных Чисел употребляет единственное изначальное значение, откуда и следует его псевдослучайность, в то время как Генератор Случайных Чисел постоянно сформировывает случайное число, имея сначала высококачественную случайную величину, которая берется из разных источников энтропии.

Энтропия — это мера кавардака. Информационная энтропия — мера неопределённости либо непредсказуемости инфы.

Выходит, что чтоб сделать псевдослучайную последовательность нам нужен метод, который будет генерить некую последовательность на основании определенной формулы. Но такую последовательность можно будет предсказать. Тем не наименее, давайте пофантазируем, вроде бы могли написать собственный генератор случайных чисел, если б у нас не было Math.random()

ГПСЧ имеет некий метод, который можно воспроизвести.
ГСЧ — это получение чисел стопроцентно из какого или шума, возможность просчитать который стремится к нулю. При всем этом в ГСЧ есть определенные методы для сглаживания распределения.

Придумываем метод ГПСЧ

Генератор псевдослучайных чисел (ГПСЧ, англ. pseudorandom number generator, PRNG) — метод, порождающий последовательность чисел, элементы которой практически независимы друг от друга и подчиняются данному распределению (обычно равномерному).

Мы можем взять последовательность каких-либо чисел и брать от их модуль числа. Самый обычный пример, который приходит в голову. Нам необходимо пошевелить мозгами, какую последовательность взять и модуль от чего же. Если просто в лоб от 0 до N и модуль 2, то получится генератор 1 и 0:

Эта функция генерит нам последовательность 01010101010101… и именовать ее даже псевдослучайной никак недозволено. Чтоб генератор был случайным, он должен проходить тест на последующий бит. Но у нас не стоит таковой задачки. Тем не наименее даже без всяких тестов мы можем предсказать последующую последовательность, означает таковой метод в лоб не подступает, но мы в подходящем направлении.

А что если взять какую-то известную, но нелинейную последовательность, к примеру число PI. А в качестве значения для модуля будем брать не 2, а что-то другое. Можно даже пошевелить мозгами на тему меняющегося значения модуля. Последовательность цифр в числе Pi считается случайной. Генератор может работать, используя числа Пи, начиная с некий неведомой точки. Пример такового метода, с последовательностью на базе PI и с изменяемым модулем:

Но в JS число PI можно вывести лишь до 48 знака и не наиболее. Потому предсказать такую последовательность все так же просто и любой пуск такового генератора будет выдавать постоянно одни и те же числа. Но наш генератор уже стал демонстрировать числа от 0 до 9. К слову, так смотрится распределение по выпадению чисел при 10000 итерациях:

Распределение весьма неравномерное, но мы получим генератор чисел от 0 до 9.

Мы можем взять не число Pi, а время в числовом представлении и это число разглядывать как последовательность цифр, при этом для того, чтоб всякий раз последовательность не повторялась, мы будем считывать ее с конца. Итого наш метод нашего ГПСЧ будет смотреться так:

Вот это уже похоже на генератор псевдослучайных чисел. И этот же Math.random() — это ГПСЧ, про него мы побеседуем чуток позднее. При всем этом у нас всякий раз 1-ое число выходит различным.

Фактически на этих обычных примерах можно осознать как работают наиболее сложные генераторы случайных числе. И есть даже готовые методы. Для примера разберем один из их — это Линейный конгруэнтный ГПСЧ(LCPRNG).

Интересно почитать:

Линейный конгруэнтный ГПСЧ

Линейный конгруэнтный ГПСЧ(LCPRNG) — это распространённый способ для генерации псевдослучайных чисел. Он не владеет криптографической стойкостью. Этот способ заключается в вычислении членов линейной рекуррентной последовательности по модулю некого натурального числа m, задаваемой последующей формулой:

где a(multiplier), c(addend), m(mask) — некие целочисленные коэффициенты. Получаемая последовательность зависит от выбора стартового числа — т.е. seed. При различных значениях seed получаются разные последовательности случайных чисел. Пример реализации такового метода на JavaScript:

Почти все языки программирования употребляют LСPRNG (но не конкретно таковой метод(!)).

Как говорилось выше, такую последовательность можно предсказать. Так для чего нам ГПСЧ? Если гласить про сохранность, то ГПСЧ — это неувязка. Если гласить про остальные задачки, то эти характеристики — могут сыграть в плюс. К примеру для разных спец эффектов и анимаций графики может пригодиться нередкий вызов random. И вот здесь важны распределение значений и перформанс! Секурные методы не могут похвастать скоростью работы.

Очередное свойство — воспроизводимость. Некие реализации разрешают задать seed, и это весьма полезно, если последовательность обязана повторяться. Проигрывание необходимо в тестах, к примеру. И еще много остальных вещей существует, для которых не нужен неопасный ГСЧ.

Как устроен Math.random()

Способ Math.random() возвращает псевдослучайное число с плавающей запятой из спектра [0, 1) , то есть, от 0 (включительно) до 1 (но не включая 1), которое затем можно отмасштабировать до нужного диапазона. Реализация сама выбирает начальное зерно для алгоритма генерации случайных чисел; оно не может быть выбрано или сброшено пользователем.

Как устроен алгоритм Math.random() — интересный вопрос. До недавнего времени, а именно до 49 Chrome использовался алгоритм MWC1616:

Именно этот алгоритм генерит нам последовательность псевдослучайных чисел в промежутке между 0 и 1.

UPD

Исправил ошибку в алгоритме MWC1616 (пропущенные скобки). Эта же ошибка повторяется и в статье https://v8project.blogspot.ru/2015/12/theres-mathrandom-and-then-theres.html

то видим, что должны быть скобки:

Предсказываем Math.random()

Чем это было чревато? Есть такой квест: https://alf.nu/ReturnTrue

В нем есть задача:

Что нужно вписать вместо вопросов, чтобы функция вернула true? Кажется что это невозможно. Но, это возможно, если вы заглядывали в спеку и видели алгоритм ГПСЧ V8. Решение этой задачи в свое время мне показал Роман Дворнов:

Этот код работал в 70% случаев для Chrome < 49 и Node.js < 5. Рома Дворнов, как всегда, показал чудеса магии, которая не что иное, как глубокое понимание внутренних механизмов браузеров. Я все жду, когда Роман сделает доклад на основе этих событий или напишет более подробную статью.

Что здесь происходит? Все дело в том, что алгоритм можно предсказать. Чтобы это было нагляднее, можно сгенерировать картинку случайных пикселей. На сайте https://bl.ocks.org/mmalone/bf59aa2e44c44dde78ac

есть такой генератор. Вот что было, когда в браузере был алгоритм MWC1616:

Видите эти равномерности на левом слайде? Изображение показывает проблему с распределением значений. На картинке слева видно, что значения местами сильно группируются, а местами выпадают большие фрагменты. Как следствие — числа можно предсказать.

Выходит что мы можем отреверсить Math.random() и предсказать, какое было загадано число на основе того, что получили в данный момент времени. Для этого получаем два значения через Math.random(). Затем вычисляем внутреннее состояние по этим значениям. Имея внутреннее состояние можем предсказывать следующие значения Math.random() при этом не меняя внутреннее состояние. Меняем код так так, чтобы вместо следующего возвращалось предыдущее значение. Собственно все это и описано в коде-решении для задачи random4. Но потом алгоритм изменили (подробности читайте в спеке). Его можно будет сломать, как только у нас в JS появится нормальная работа с 64 битными числами. Но это уже будет другая история.

Новый алгоритм выглядит так:

Его все так же можно будет просчитать и предсказать. Но пока у нас нет “длинной математики” в JS. Можно попробовать через TypedArray сделать или использовать специальные библиотеки. Возможно кто-то однажды снова напишет предсказатель. Возможно это будешь ты, читатель. Кто знает ?

Сrypto Random Values

Метод Math.random() не предоставляет криптографически стойкие случайные числа. Не используйте его ни для чего, связанного с безопасностью. Вместо него используйте Web Crypto API (API криптографии в вебе) и более точный метод window.crypto.getRandomValues() .

Пример генерации случайного числа:

Но, в отличие от ГПСЧ Math.random(), этот метод очень ресурсоемкий. Дело в том, что данный генератор использует системные вызовы в ОС, чтобы получить доступ к источникам энтропии (мак адрес, цпу, температуре, etc…).

Материалы про Math.random()

Больше про random в спецификации:

Хорошая статья про работу рандомайзера

Пример реализации предсказателя с Math.random()

Кстати, следить за обновлениями и прочими материалами от меня можно в телеграм канале: @prowebit

В этом канале публикую не только статьи из этого блога, но и различные новости и мысли. Подписывайтесь ?

Генерация случайных чисел в javascript.

В javascript часто требуется сгенерировать случайное число. Например, чтобы нарисовать звезду в ночном небе или анимировать хаотические аттракторы. Однако существуют различные способы генерации, и от приложения зависит, какой вы будете использовать.

Базовая генерация

Самый простой способ получить случайное число — это метод Math.random(), встроенный в javascript.

Math.random() всегда возвращает число с плавающей точкой между 0 и 1.

Технически, число, которое вы получите, может быть 0, но никогда не будет точно 1.

Посколько это используется достаточно часто, Math.random() помещают внутрь функции

function getRandom() <
return Math.random();
>

Проблема, конечно, заключается в том, что функция всегда будет создавать случайное число в пределах очень ограниченного диапазона. Большинство других рецептов на этой странице предназначены для того, чтобы решить эту проблему.

Генерация между числами: минимальные и максимальные значения

Чтобы добавить эту функциональность, нам потребуется немного математики.

FLOATING POINT

function getRandomFloat(min, max) <
return Math.random() * (max — min) + min;
>
getRandomFloat(11, 101)
> 75.31898734299466

function getRandomInt(min, max) <
return Math.floor(Math.random() * (max — min)) + min;
>

getRandomInt(10, 20)
> 12

Случайное целое число в диапазоне, включая минимальное и максимальное.

function getRandomInRange(min, max) <
return Math.floor(Math.random() * (max — min + 1)) + min;
>

getRandomInRange(1, 10)
> 7

Подбрасывание монеты(случайное true или false)

Если вам нужно получить просто 0 или 1, то используйте следующий код:

function coinToss() <
return Math.floor(Math.random() * 2);
>
coinToss();
> 0

Интересно почитать: В excel поиск значения в массиве

Если нужно конкретно true или false

function coinToss() <
return (Math.floor(Math.random() * 2) === 0);
>
coinToss();
> true

Если вам нужно ассоциировать любые слова со сторонами монеты

function coinFlip() <
return (Math.floor(Math.random() * 2) === 0) ? «up» : «down»;
>
coinToss();
> up

Генерация с исключениями

Для ограниченного диапазона целых чисел: создайте массив чисел, которые вы бы хотели вырисовывать, и выберите из него случайное.

var numPool = [ 1, 3, 5, 7, 9, 10 ],
rand = numPool[Math.floor(Math.random() * numPool.length)];

Для чего-нибудь наиболее оживленного: добавьте массив целых чисел, которые вы желаете исключить, и пустой массив, который будет содержать итог фильтрации первого массива во 2-ой.

var numPool = [ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 ];
var excludePool = [ 3, 4 ];
var filteredPool = [];

Потом сделайте цикл по массиву numPool, проверьте, есть ли случайное число в массиве исключений excludePool, и расположите итог в массив filteredPool:

В конце концов, отобразите случайное число из отфильтрованного массива

var rand = filteredPool[Math.floor(Math.random() * filteredPool.length)];

Генерация случайного, неповторяющегося числа

Для маленьких наборов чисел: сделайте массив, заполненный элементами, перетасуйте их случайным образом, расположите итог в новейший массив, потом достаньте перетасованные элементы один раз:

var numPool = [ 13, 21, 36, 14, 27, 10 ];

function shuffle(numPool) <
for(var j, x, i = numPool.length; i; j = parseInt(Math.random() * i), x = numPool[—i], numPool[i] = numPool[j], numPool[j] = x);
return numPool;
>;
var randomResult = shuffle(numPool);
while( randomResult.length > 0 ) <
console.log( randomResult.pop() );
>

Для наиболее огромных наборов чисел: сделайте и заполните массив случайными целыми числами, отклоняя хоть какое, которое уже было ранее сгенерировано:

var numReserve = []
while (numReserve.length

В коде выше numReserve заполнен 12 случайными числами меж 0 и 1000. Числа потом могут быть получены из массива.

Тайнопись

Всех показанных выше способов будет недостаточно для сотворения криптографически защищенных функций. Для этого мы можем применять Web Cryptography API, создав типизированный массив:

var cryptoStor = new Uint16Array(8);

В этом случае мы создаем массив с 8 разными слотами, любой из которых может содержать 16-битовое целое число без знака. Остальные функции включают Int8Array, Uint8Array, int16Array, Int32Array и Uint32Array.

Сейчас заполните массив случайными числами определенного типа

Показаны избранные значения в консоли:

> [43484, 57947, 46691, 49849, 24272, 11827, 28203, 17423]

Web Cryptography API имеет неплохую поддержку в современных браузерах, хотя в неких необходимо ставить префиксы.

Копирование материалов разрешается лишь с указанием создателя (Миша Русаков) и индексируемой прямой ссылкой на веб-сайт (http://myrusakov.ru)!

Добавляйтесь ко мне в друзья ВКонтакте: http://vk.com/myrusakov.
Если Вы желаете отдать оценку мне и моей работе, то напишите её в моей группе: http://vk.com/rusakovmy.

Если Вы не желаете пропустить новейшие материалы на веб-сайте,
то Вы сможете подписаться на обновления: Подписаться на обновления

Если у Вас остались какие-либо вопросцы, или у Вас есть желание высказаться по поводу данной нам статьи, то Вы сможете бросить собственный комментарий понизу странички.

Посоветуйте эту статью друзьям:

Если Для вас приглянулся веб-сайт, то разместите ссылку на него (у себя на веб-сайте, на форуме, в контакте):

Она смотрится вот так:

Комменты ( 5 ):

Здрасти! Можно вопросец не по теме статьи?

Естественно, можно! Но задайте его, пожалуйста, в службу саппорта: http://support.myrusakov.ru/

Спасибо! В последующий раз, уже ответили на javascript.ru

Отлично! Рады за вас!

не чего же не вывелось Случайное целое число в спектре, включая малое и наибольшее. function getRandomInRange(min, max) < return Math.floor(Math.random() * (max - min + 1)) + min; >getRandomInRange(1, 10) > 7

Для прибавления объяснений нужно войти в систему.
Если Вы ещё не зарегистрированы на веб-сайте, то поначалу зарегайтесь.

Способ random — Возвращает случайное число — Генерация случайных чисел

В JavaScript нередко возникает ситуация, когда для выполнения какого-нибудь скрипта нужно получить случайное число. Для этого следует пользоваться способом random объекта Math .

Способ random — Случайное число от 0 до 1

По дефлоту способ random объекта Math генерирует (возвращает) случайное число от 0 до 1 .

var any = Math . random (); /* Генерируем число от 0 до 1 */

document. write ( any );

Но по сути почти всегда внедрение способа random в чистом виде не имеет смысла , потому что дробное число от 0 до 1 с огромным количеством символов опосля запятой очень изредка применимо.

Способ random — Случайное число от 0 до 100

Способ random может генерировать случайные числа от 0 до 100 . Разглядим пример, как это создать.

var any = Math . random () * 100 ; /* Генерируем число от 0 до 100 */

document. write ( any );

Как видно из примера, для того чтоб сгенерировать случайное число от 0 до 100 с помощью способа random , необходимо скрипт для генерации чисел от 0 до 1 помножить на 100 .

Да и этот вариант работы способа random снова же фактически бесполезен, потому что, на самом деле, мы имеем все тоже дробное число, что и в прошлом примере. В то время как для работы скриптов в главном требуется генерация целых чисел .

Тут приходят на помощь способы round , floor либо ceil из предшествующей заметки, которые разрешают округлять дробные числа.

var any = Math . random () * 100 ; /* Генерируем число от 0 до 100 */

document. write ( Math . round (any) ); /* Округляем сгенерированное число */

Вот таковым образом с помощью способов random и round объекта Math поначалу генерируется , а позже округляется случайное число от 0 до 100 .

Заместо 100 можно указать хоть какое другое число , к примеру, 40 либо 400 и т.д. Тогда способ random будет выдавать случайные числа в спектре от 0 до хоть какого обозначенного.

Скрипт для генерации чисел из ПРОИЗВОЛЬНОГО спектра

В прошлом примере мы удостоверились в том, что способ random вкупе с одним из способов округления может генерировать случайные целые числа в спектре от 0 до хоть какого обозначенного числа .

При всем этом мы имеем дело с достаточно обычным javascript -кодом.

Но что если необходимо сгенерировать число в случайном спектре , т.е. в таком, где 1-ое число непревзойденно от 0 ?

Для этого существует определенный скрипт. Смотрим пример ниже.

function myRandom ( from , to )

<
return Math . floor (( Math . random () * ( to — from + 1 )) + from ); /* Оператор return возвращает итог работы функции */
>