Как отсортировать в Powershell объекты через Sort-Object

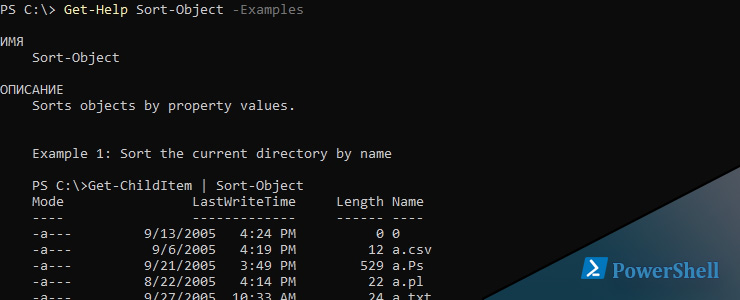
Для сортировки в Powershell есть командлет Sort-Object. Мы можем отсортировать хоть какой вывод установок, в том числе массивы, хэш таблицы и по датам. Любой вариант мы разглядим на примерах.

По дефлоту командлет сортирует по возрастанию (ASC). На примере ниже я получил данные по отклику микропроцессора:

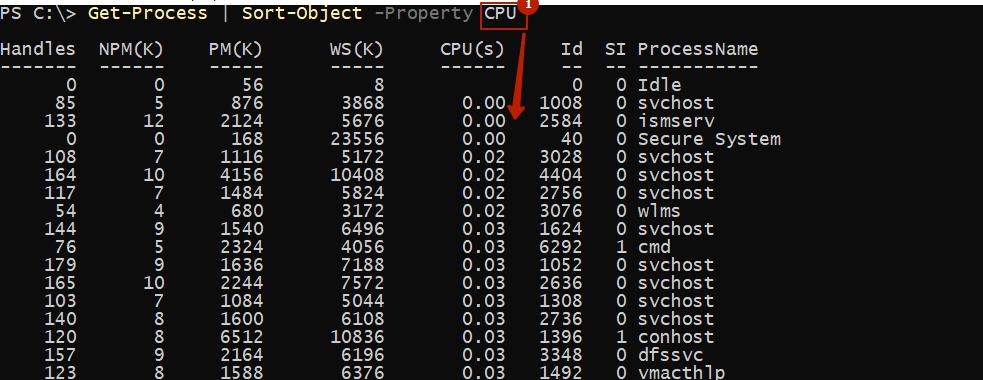
Ключ Property допускает внедрение нескольких значений.

Если нам необходимо выполнить сортировку по убыванию (DESC), то для этого есть последующий ключ:

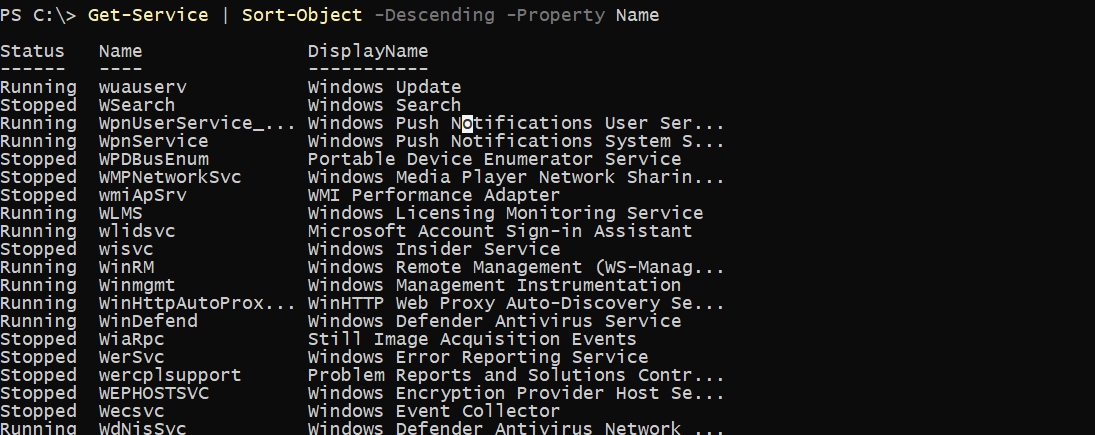
Если у нас не указан ключ Descending, то у нас будет таковая последовательность вывода:

1. Числа
2. Буковкы британского алфавита
3. Буковкы российского алфавита

Сортировка массивов и дат в Powershell Sort-Object

По сути хоть какой объект сортируется аналогично предшествующим примерам. Если мы собираемся выполнить в Powershell сортировку по дате необходимо убедиться, что необходимое свойство имеет формат Datetime.

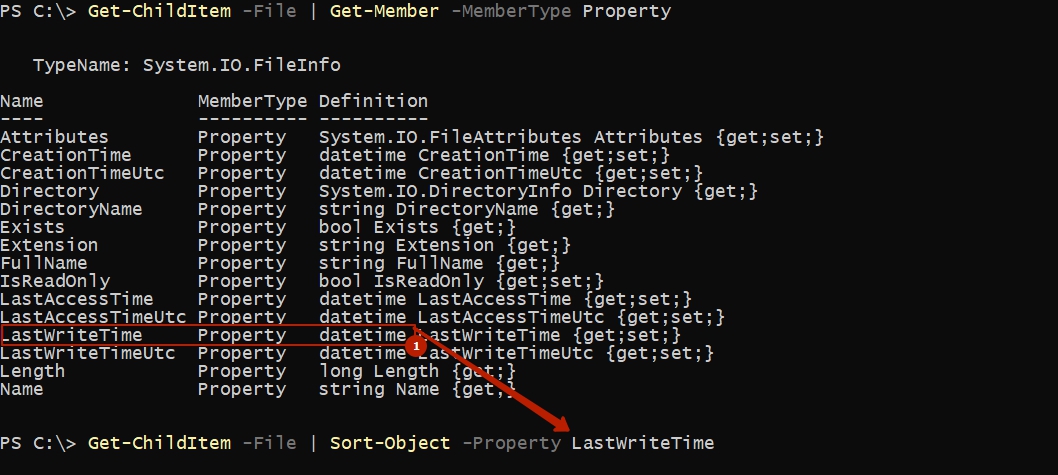
Случается так, что дата формата INT (численный) либо STR (строковый) и если вы не желаете сортировать как числа либо строчки, то их необходимо конвертировать. Для примера так я отсортирую по типу данных datetime преобразовав число:

Как переименовывать папки в Powershell

Пример с сортировкой массива:

Хэш таблцицы сортируются так же.

Доп характеристики сортировки в Powershell

Хоть это и не много относится к сортировке, то у нас есть возможность получить неповторимые значения в выводе:

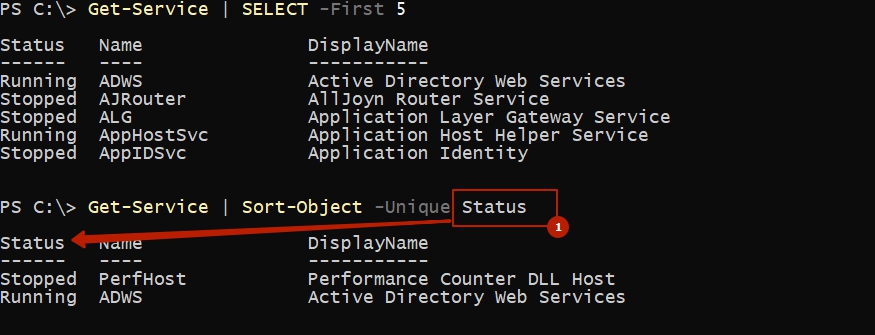
Для сортировки с учетом регистра букв есть ключ CaseSensitive, но он похоже не работает ( как минимум в PS 5.1 ).

Компьютерная грамотность с Надеждой

Заполняем пробелы — расширяем горизонты!

Обычная сортировка текста в Ворде при помощи таблицы

Почти все юзеры компа встречались с неувязкой, когда требуется сортировка текста в Ворде по алфавиту от А до Я либо напротив, от Я до А.

Давайте представим, что в некоей школе есть класс, в котором обучается 7 учеников. Естественно, в настоящей школе учеников обычно бывает больше. Но допустим, что учеников всего 7 человек, и ниже показан перечень их имен, записанный в редакторе Microsoft Word (рис. 1).

Рис. 1. Перечень имен, которые требуется отсортировать в алфавитном порядке.

Как показанный перечень переработать в редакторе текста Word так, чтоб имена были в алфавитном порядке? Вручную переписывать? Выделять каждое имя в отдельности и перетаскивать мышкой на необходимое пространство в перечне?

Положим, если имен либо фамилий всего 7, то схожее ручное перетаскивание полностью может быть. А если список имен будет большенный, допустим, человек 50?

Предлагаю разглядеть способности не ручной, а автоматической сортировки текстов в Ворде. Можно за три шага сделать сортировку в Ворде по алфавиту (по возрастанию либо по убыванию).

Преобразование текста Word в таблицу: шаг 1-ый

Выделяем список имен, которые необходимо автоматом расположить в том либо ином порядке. Выделение делается левой клавишей мышки, которую необходимо надавить и задерживать в ходе выделения фрагмента текста. На рисунке 1 имена показаны уже, как выделенные.

Дальше на вкладке «Вставка» (1 на рис. 2) избираем опцию «Таблица» (2 на рис. 2). И кликаем по строке меню «Конвертировать в таблицу» (3 на рис. 2).

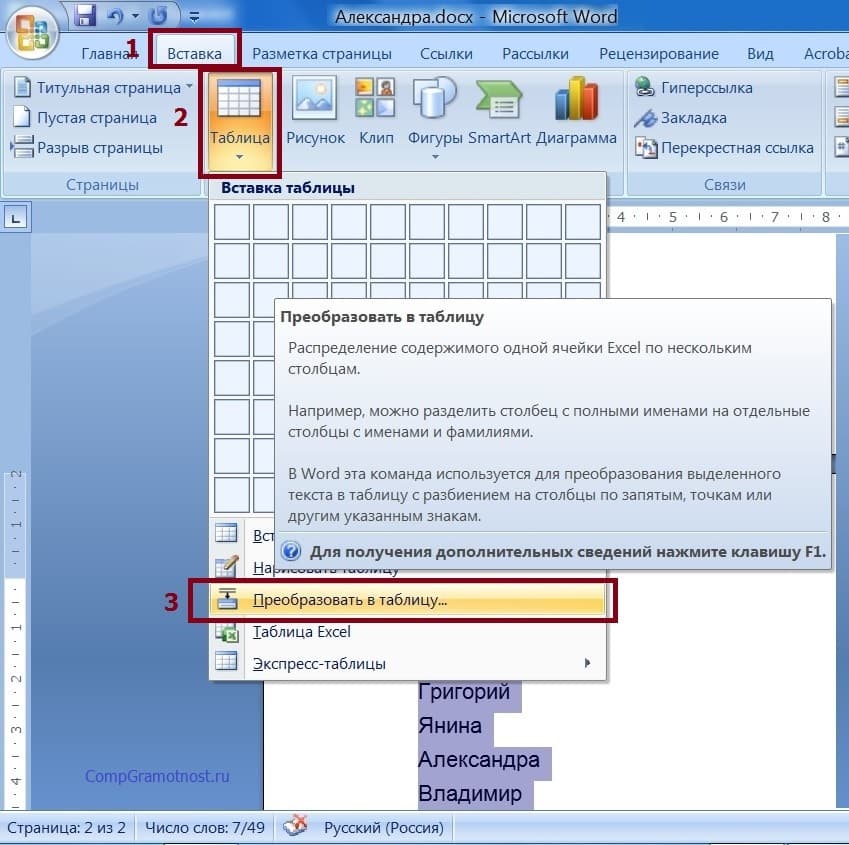
Рис. 2. Преобразование текста, подлежащего сортировке, в таблицу.

Для чего потребовалась таблица? Дело в том, что

в Ворде можно изменять сортировку данных лишь в таблицах.

Конкретно потому поначалу требуется конвертировать текст в таблицу, и лишь позже делать сортировку данных.

Следом в открывшемся служебном окне «Конвертировать в таблицу» (рис. 3) остается только кликнуть на клавишу «ОК» (1 на рис. 3), особо не вчитываясь в содержание предлагаемых опций. Опции по умолчанию выставлены так, как требуется в данном определенном случае. Поэтому довольно надавить ОК, что практически значит «согласны».

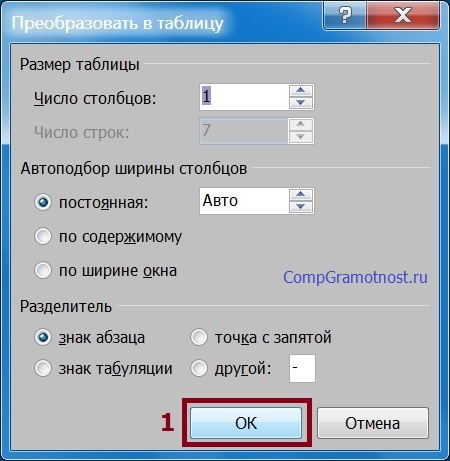
Рис. 3. Доказательство опций по умолчанию для следующего перевоплощения выделенного текста в таблицу.

Выделенный перечень имен здесь же перевоплотится в таблицу. Ничего ужасного, что заместо обычного текста возникла какая-то расчерченная на графы таблица. Позже настолько же просто можно будет перевоплотить таблицу в текст, как будет выполнена сортировка данных.

Сортировка текста в Ворде по алфавиту: шаг 2-ой

Нам необходимо расположить имена в таблице в алфавитном порядке. Для этого пригодится в меню «Макет» (1 на рис. 4) кликнуть по кнопочке «Сортировка» (2 рис. 4). При всем этом принципиально сохранить выделение таблицы. Голубий цвет, в который «окрашена» таблица на рис. 4, свидетельствует о том, что она выделена в редакторе Word.

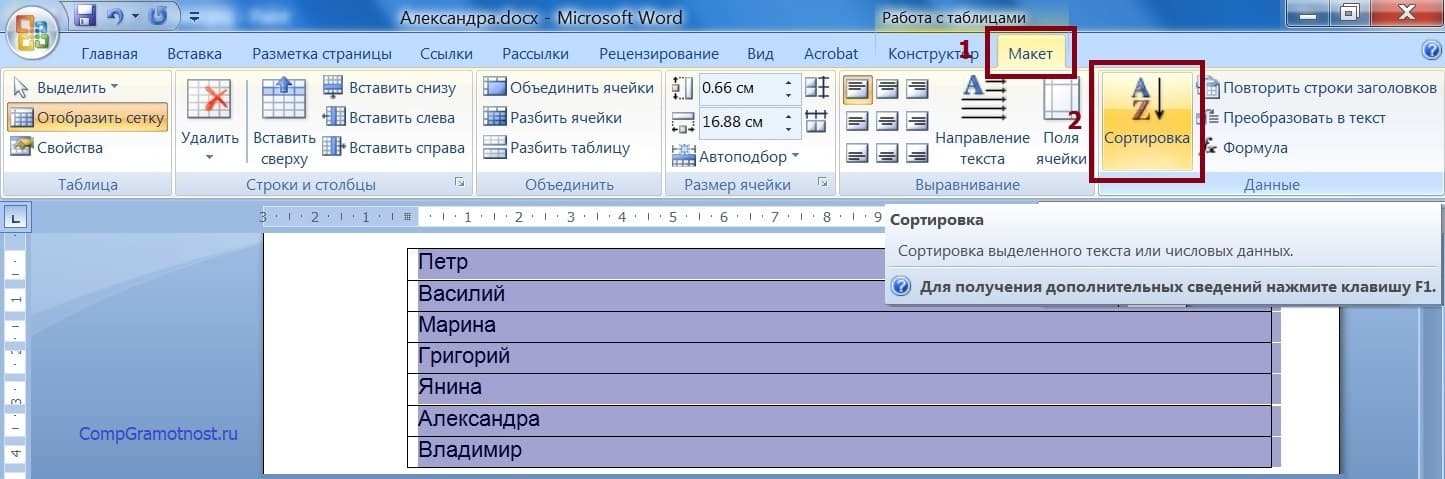
Рис. 4. Сортировка данных по алфавиту в выделенной таблице Word.

На дисплее покажется служебное меню «Сортировка» (рис. 5). Оно довольно сложное, содержит много настроечных характеристик. Но нам пригодятся лишь 2 из их, которые к тому же не надо вводить вручную, характеристики уже указаны.

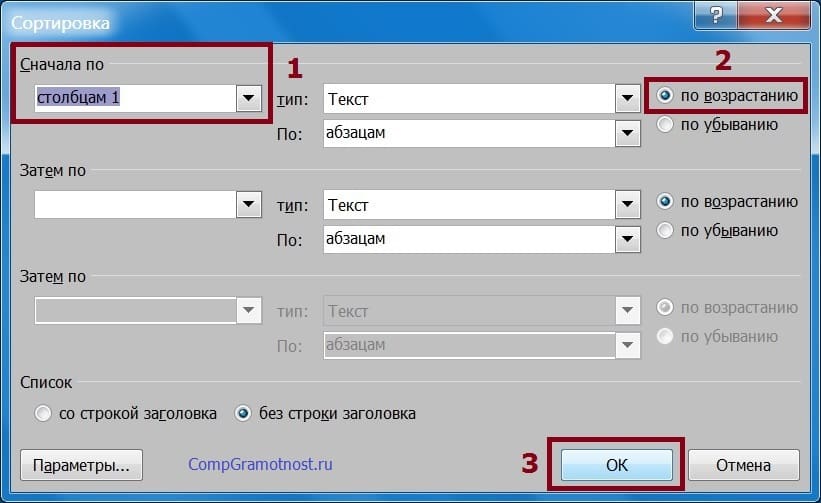
Рис. 5. Опции характеристик сортировки данных в таблице Ворд.

В окошке опций «Поначалу по» (красноватая цифра 1 на рис. 5) стоит параметр «столбцам 1». Справа от данной надписи на самом краю окна проставлено выделение «по возрастанию» (2 на рис. 5).

При желании «по возрастанию» можно без помощи других поменять на «по убыванию». Тогда данные будут отсортированы по алфавиту не от буковкы «а» до буковкы «я», а в обратном направлении: от «я» до «а». Пока же оставим все как есть и кликнем по кнопочке «ОК» (3 на рис. 5).

Опосля клика по «ОК» сходу же увидим, что имена выстроились так, как требовалось (рис. 6). На первом месте оказалась «Александра», так как имя начинается с «а». На крайнем месте в таблице стоит «Янина», поэтому что 1-ая буковка в ее имени – это «я».

Преобразование отсортированной таблицы в текст в Ворде: шаг 3-ий

Имена, расположенные в алфавитном порядке, стоят по-прежнему в таблице, а не в виде текста, как было вначале. Поэтому на крайнем шаге преобразований выполним оборотное действие по превращению таблицы в текст Ворда.

Для перевоплощения таблицы в текст, не снимая выделения таблицы, на вкладке «Макет» (цифра 1 на рисунке 6) кликаем по кнопочке «Данные» (2 на рис. 6). И избираем опцию «Конвертировать в текст» (3 на рисунке 6).

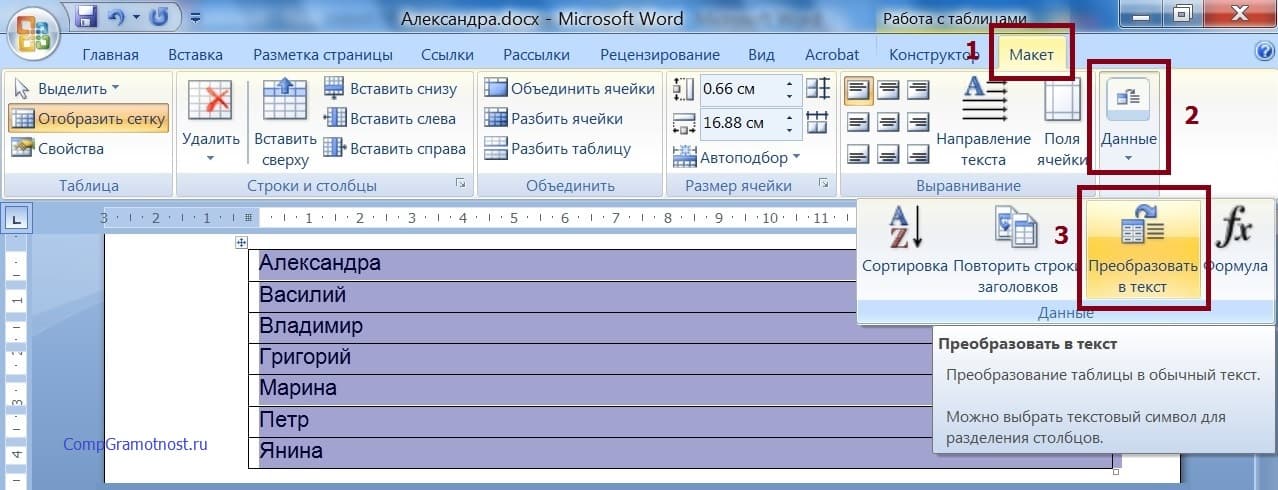
Рис. 6. Оборотное преобразование таблицы в текст Ворд.

Опять покажется служебное окно опций характеристик. Сейчас предлагаются функции для преобразования таблицы в текст (рис. 7). В открывшемся служебном окне довольно только надавить на клавишу «ОК» (1 на рис. 7), так как все опции выставлены по умолчанию так, как необходимо.

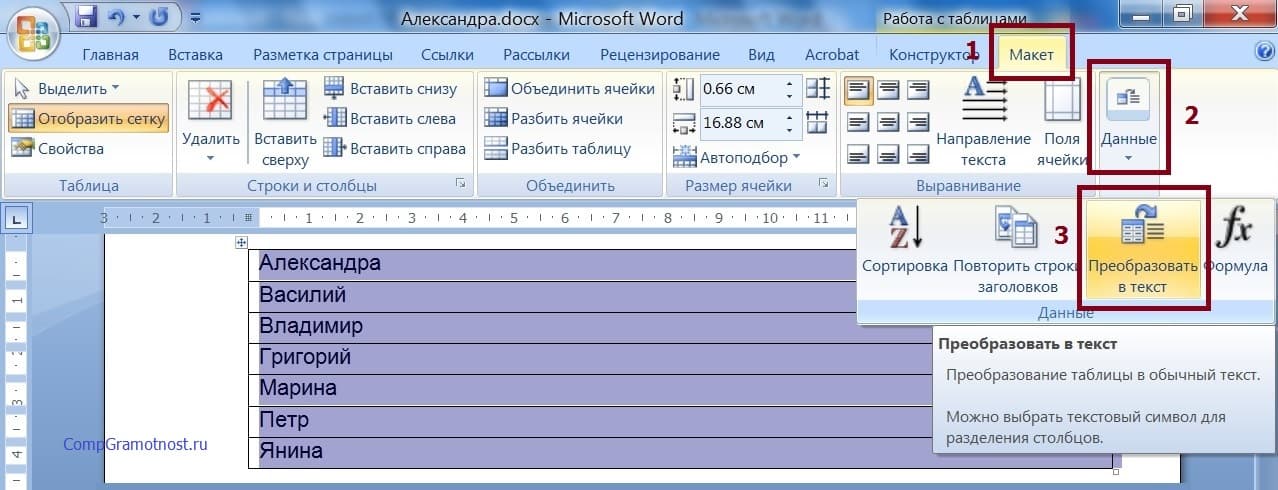
Рис. 7. Служебное окно опций характеристик преобразования таблицы в текст Ворд.

Итак, кликаем по «ОК» (1 на рис. 7) и… лицезреем на дисплее текст, состоящий из прежних имен, но уже расположенных в строго алфавитном порядке (рис. 8). Что и требовалось сделать в конечном итоге! Cортировка текста в Ворде проведена.

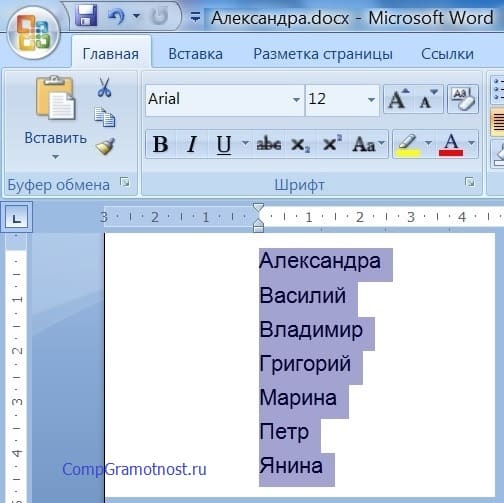
Рис. 8. Окончательное размещение имен по алфавиту опосля всех сделанных действий в редакторе Ворд.

Итоги

Очевидно, таковым же образом можно отсортировать перечень имен либо фамилий, либо даже еще наиболее длинноватые тексты (к примеру, вполне ФИО). При этом перечень быть может хоть какой величины, не непременно 7 имен, как в показанном примере.

Можно схожим образом расположить в алфавитном порядке хоть 70, хоть 700, хоть 7000 имен. Да что там имена, фамилии либо ФИО! Так можно отсортировать любые тексты. Основное, чтоб эти тексты были размещены в Word друг под другом, абзац за абзацем.

Сможете испытать – всё получится!

Видео-формат статьи

Сортировка подсчётом

Сортировка подсчётом (англ. counting sort) — метод сортировки целых чисел в спектре от [math]0[/math] до некой константы [math]k[/math] либо сложных объектов, работающий за линейное время.

Содержание

Сортировка целых чисел [ править ]

Это простой вариант метода.

Описание [ править ]

Начальная последовательность чисел длины [math]n[/math] , а в конце отсортированная, хранится в массиве [math]A[/math] . Также употребляется вспомогательный массив [math]C[/math] с индексами от [math]0[/math] до [math]mathrm k — 1[/math] , вначале заполняемый нулями.

• Поочередно пройдём по массиву [math]A[/math] и запишем в [math]C[i][/math] количество чисел, равных [math]i[/math] .

• Сейчас довольно пройти по массиву [math]C[/math] и для всякого [math]number in <0, . mathrm k - 1>[/math] в массив [math]A[/math] поочередно записать число [math]number[/math] [math] C[number][/math] раз.

Псевдокод [ править ]

Сортировка сложных объектов [ править ]

Сортировка целых чисел за линейное время это отлично, но недостаточно. Время от времени бывает весьма лучше применить резвый метод сортировки подсчетом для упорядочивания набора каких-то «сложных» данных. Под «сложными объектами» тут предполагаются структуры, содержащие в для себя несколько полей. Одно из их мы выделим и назовем ключом, сортировка будет идти конкретно по нему (предполагается, что значения, принимаемые ключом — целые числа в спектре от [math]0[/math] до [math]mathrm k-1[/math] ).

Мы не сможем применять тут в точности этот же метод, что и для сортировки подсчетом обыденных целых чисел, поэтому что в наборе могут быть разные структуры, имеющие однообразные ключи. Существует два метода совладать с данной неувязкой — применять списки для хранения структур в отсортированном массиве либо заблаговременно посчитать количество структур с схожими ключами для всякого значения ключа.

Описание [ править ]

Начальная последовательность из [math]n[/math] структур хранится в массиве [math]A[/math] , а отсортированная — в массиве [math]B[/math] такого же размера. Не считая того, употребляется вспомогательный массив [math]P[/math] с индексами от [math]0[/math] до [math]mathrm k-1[/math] .

Мысль метода состоит в подготовительном подсчете количества частей с разными ключами в начальном массиве и разделении результирующего массива на части соответственной длины (будем именовать их блоками). Потом при повторном проходе начального массива любой его элемент копируется в специально отведенный его ключу блок, в первую вольную ячейку. Это осуществляется при помощи массива индексов [math]P[/math] , в котором хранятся индексы начала блоков для разных ключей. [math]P[key][/math] — индекс в результирующем массиве, соответственный первому элементу блока для ключа [math]key[/math] .

• Пройдем по начальному массиву [math]A[/math] и запишем в [math]P[i][/math] количество структур, ключ которых равен [math]i[/math] .

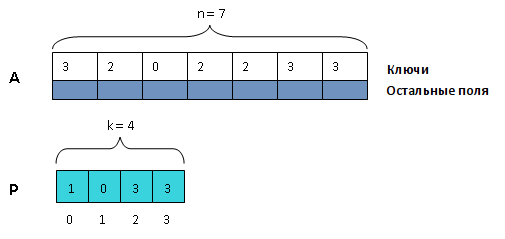
• На уровне мыслей разобьем массив [math]B[/math] на [math]k[/math] блоков, длина всякого из которых равна соответственно [math]P[0][/math] , [math]P[1][/math] , . [math]P[k][/math] .

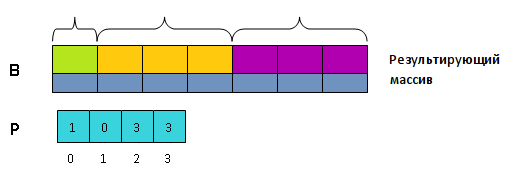
• Сейчас массив [math]P[/math] нам больше не нужен. Превратим его в массив, хранящий в [math]P[i][/math] сумму частей от [math]0[/math] до [math]i-1[/math] старенького массива [math]P[/math] .

• Сейчас «сдвинем» массив [math]P[/math] на элемент вперед: в новеньком массиве [math]P[0] = 0[/math] , а для [math]i gt 0[/math] [math]P[i] = P_[i-1][/math] , где [math]P_[/math] — старенькый массив [math]P[/math] .
  Это можно сделать за один проход по массиву [math]P[/math] , при этом сразу с предшествующим шагом.
  Опосля этого деяния в массиве [math]P[/math] будут хранится индексы массива [math]B[/math] . [math]P[key][/math] показывает на начало блока в [math]B[/math] , соответственного ключу [math]key[/math] .

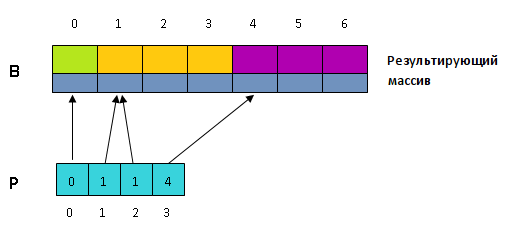
• Произведем саму сортировку. Снова пройдем по начальному массиву [math]A[/math] и для всех [math]i in [0, n-1][/math] будем помещать структуру [math]A[i][/math] в массив [math]B[/math] на пространство [math]P[A[i].key][/math] , а потом наращивать [math]P[A[i].key][/math] на [math]1[/math] . Тут [math]A[i].key[/math] — это ключ структуры, находящейся в массиве [math]A[/math] на [math]i[/math] -том месте.

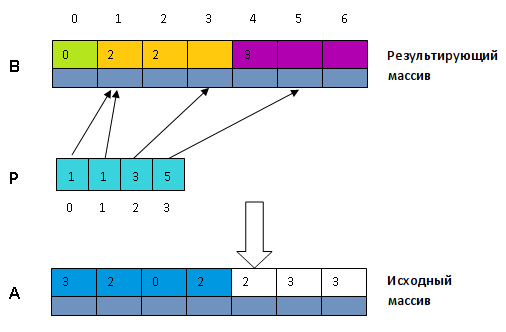
Таковым образом опосля окончания метода в [math]B[/math] будет содержаться начальная последовательность в отсортированном виде (потому что блоки размещены по возрастанию соответственных ключей).

Стоит также отметить, что эта сортировка является устойчивой, потому что два элемента с схожими ключами будут добавлены в том же порядке, в каком просматривались в начальном массиве [math]A[/math] . Благодаря этому свойству существует цифровая сортировка.

Псевдокод [ править ]

Тут [math]A[/math] и [math]B[/math] — массивы структур размера [math]n[/math] , с индексами от [math]0[/math] до [math]n-1[/math] . [math]P[/math] — целочисленный массив размера [math]k[/math] , с индексами от [math]0[/math] до [math]k-1[/math] , где [math]k[/math] — количество разных ключей.

Тут шаги 3 и 4 из описания объединены в один цикл. Направьте внимание, что в крайнем цикле аннотацией

копируется структура [math]A[i][/math] полностью, а не только лишь её ключ.

Анализ [ править ]

В первом методе 1-ые два цикла работают за [math]Theta(k)[/math] и [math]Theta(n)[/math] , соответственно; двойной цикл за [math]Theta(n + k)[/math] . Метод имеет линейную временную трудоёмкость [math]Theta(n + k)[/math] . Применяемая доборная память равна [math]Theta(k)[/math] .

2-ой метод состоит из 2-ух проходов по массиву [math]A[/math] размера [math]n[/math] и 1-го прохода по массиву [math]P[/math] размера [math]k[/math] . Его трудозатратность, таковым образом, равна [math]Theta(n + k)[/math] . На практике сортировку подсчетом имеет смысл использовать, если [math]k = O(n)[/math] , потому можно считать время работы метода равным [math]Theta(n)[/math] .
Как и в обыкновенной сортировке подсчетом, требуется [math]Theta(n + k)[/math] доборной памяти — на хранение массива [math]B[/math] размера [math]n[/math] и массива [math]P[/math] размера [math]k[/math] .

Метод работает за линейное время, но является псевдополиномиальным.

Поиск спектра ключей [ править ]

Если спектр значений не известен заблаговременно, то его можно отыскать при помощи линейного поиска минимума и максимума в начальном массиве, что не воздействует на асимптотику метода.
Необходимо учесть, что минимум быть может отрицательным, в то время как в массиве [math]P[/math] индексы от [math]0[/math] до [math]k-1[/math] . Потому при работе с массивом [math]P[/math] из начального [math]A[i][/math] нужно вычитать минимум, а при оборотной записи в [math]B[i][/math] добавлять его.