Матрица в Excel

Excel – это сделанная компанией Microsof программка, созданная для работы с электрическими таблицами.

Введение

Матрица представляет собой набор ячеек, которые размещаются поочередно одна за иной и показываются как прямоугольник. Операции с матрицами в Excel производятся аналогично работе со обычным спектром памяти. Все матрицы владеют отдельным адресом, который записывается так же, как и спектр. Поначалу указывается адресок первой ячейки спектра, которая размещается вверху в левом углу. Дальше записывается адресок крайней ячейки, расположенной в нижнем правом углу.

Формулы массива

Матрица, на самом деле, является массивом и для работы с ними используются надлежащие формулы. Основным их различием от обычных формул считается то, что обыденные обычные формулы могут вывести лишь одну величину. Чтоб применять формулы работы с массивами, следует выполнить таковой набор операций:

Выполнить выделение участка ячеек, куда следует вывести значения.
Задать требуемую формулу для вычислений.
Надавить клавишный набор Ctrl + Shift +Enter.

По окончанию этих процедур в поле для ввода отобразится формула массива. Она различается от обычной формулы наличием фигурных скобок. Чтоб отредактировать либо удалить формулу работы с массивом, необходимо создать выделение подходящего спектра и выполнить корректировку. Для редактирования самой матрицы используются те же композиции кнопок, что и при её формировании.

Операции с матрицами

Операция подмены местами строк и столбцов именуется транспонированием. Перед началом данной для нас процедуры, нужно выполнить выделение отдельной зоны, имеющей число строк равное числу столбцов преобразуемой матрицы, и то же самое относительно столбцов. Существует два метода выполнения транспонирования. Согласно первому способу нужно выполнить последующие деяния:

Необходимо выполнить выделение матрицы и создать её копию.
Выполнить выделение спектра ячеек для вставки транспонируемого спектра.
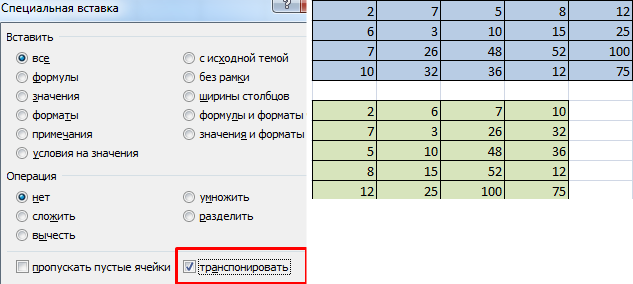
Открыть окно «Особая вставка».
Избрать клавишу «Транспонировать» и надавить ОК.

Готовые работы на аналогичную тему

2-ой метод заключается в последующем. Необходимо выполнить выделение ячейки, находящейся в левом верхнем углу спектра, выделенного для транспонируемой матрицы. Дальше следует открыть диалоговое окно с набором функций и избрать функцию ТРАНСП.

Набросок 1. Окно программки. Автор24 — интернет-биржа студенческих работ

В качестве параметра функции употребляется спектр, соответственный изначальной матрице. Но опосля того, как будет нажата кнопка ОК, покажется сообщение о ошибке, так как вставляемая функция не определена в качестве формулы массива. Другими словами дальше нужно создать последующее:

Выполнить выделение набора ячеек, созданных для транспонируемой матрицы.
Надавить клавишу F2.
Надавить набор кнопок Ctrl + Shift + Enter.

Главным преимуществом такового метода будет то, что транспонированная матрица сходу способна корректировать заложенную в неё информацию, по мере внесения коррекций в начальную матрицу.

Дальше разглядим операцию сложения. Эта операция допустима лишь для тех диапазонов, которые имеют однообразное число компонент. По другому говоря, матрицы, подлежащие сложению, должны иметь один и этот же размер. Пример представлен на рисунке ниже:

Набросок 2. Пример. Автор24 — интернет-биржа студенческих работ

В итоговой матрице нужно создать выделение первой ячейки и задать последующую формулу:

= Исходный компонент первой матрицы + Исходный компонент 2-ой матрицы

Потом следует подтвердить задание формулы кнопкой Enter и применить функцию авто наполнения (квадрат в нижнем правом углу) для копирования всех величин в новейшую матрицу. Результат приведён на рисунке ниже:

Набросок 3. Результат. Автор24 — интернет-биржа студенческих работ

Дальше разглядим операцию умножения. Имеется последующая таблица, все элементы которой нужно помножить на двенадцать:

Набросок 4. Таблица. Автор24 — интернет-биржа студенческих работ

Сущность способа умножения подобна сложению, но тут необходимо все ячейки матрицы помножить на двенадцать и результат также отразить в отдельной матрице. Нужно держать в голове о указании абсолютных ссылок на ячейки. В итоге получаем формулу:

И результирующую матрицу:

Набросок 5. Результирующая матрица. Автор24 — интернет-биржа студенческих работ

Разглядим пример перемножения матриц. Это может быть лишь при соблюдении 1-го условия. Нужно, чтоб число строк и столбцов у этих матриц являлось зеркально схожим, другими словами число столбцов приравнивалось числу строк.

Набросок 6. Перемножение матриц. Автор24 — интернет-биржа студенческих работ

Для удобства можно выделить спектр итоговой матрицы. Следует поместить курсор на ячейку в левом верхнем углу и задать последующую формулу:

Дальше следует надавить комбинацию кнопок Ctrl + Shift + Enter, чтоб узреть результат:

Набросок 7. Результат. Автор24 — интернет-биржа студенческих работ

Дальше разглядим пример оборотной матрицы. Если матрица (её спектр) квадратной формы, другими словами число ячеек по вертикали равно числу ячеек по горизонтали, то означает, по мере необходимости, можно найти оборотную матрицу. Это можно создать с помощью функции МОБР. Поначалу необходимо создать выделение первой ячейки матрицы, куда будет вставлена оборотная матрица. В неё необходимо ввести формулу:

В качестве аргумента необходимо указать спектр, для которого следует сформировать оборотную матрицу. Дальше необходимо применять комбинацию кнопок Ctrl + Shift + Enter.

Набросок 8. Окно программки. Автор24 — интернет-биржа студенческих работ

Дальше разглядим нахождение определителя матрицы. Определителем матрицы является число, определяемое для квадратной матрицы по данной формуле. Для данной для нас цели в программке Excel есть особая функция МОПРЕД. Нужно установить курсор на всякую ячейку матрицы и задать функцию:

Дальше разглядим ещё один пример вычислений. Имеется матрица А, размером три на четыре. Есть, так же, некое число k, записанное вне матрицы. Когда будет выполнена операция умножения матрицы на это число, возникнет спектр величин, который имеет такие же размеры, но все его составляющие умножены на k:

Набросок 9. Окно программки. Автор24 — интернет-биржа студенческих работ

Спектр B3:E5 является начальной матрицей, подлежащей умножению на число k, расположенному в клеточке H4. Итоговая матрица будет размещаться в спектре K3:N5. Начальная матрица обозначается как А, а итоговая как В. Итоговая матрица В будет образована умножением матрицы А на величину k. Формула для вычислений записывается в ячейку К3:

Функции для работы с матрицами в Excel

В программке Excel с матрицей можно работать как с спектром. Другими словами совокупой смежных ячеек, занимающих прямоугольную область.

Адресок матрицы – левая верхняя и правая нижняя ячейка спектра, обозначенные черед двоеточие.

Формулы массива

Построение матрицы средствами Excel в большинстве случаев просит внедрение формулы массива. Основное их отличие – результатом становится не одно значение, а массив данных (спектр чисел).

Порядок внедрения формулы массива:

Выделить спектр, где должен показаться итог деяния формулы.
Ввести формулу (как и положено, со знака «=»).
Надавить сочетание клавиш Ctrl + Shift + Ввод.

Интересно почитать: Диаграмма каскадная в excel

В строке формул отобразится формула массива в фигурных скобках.

Чтоб поменять либо удалить формулу массива, необходимо выделить весь спектр и выполнить надлежащие деяния. Для введения конфигураций применяется та же композиция (Ctrl + Shift + Enter). Часть массива поменять нереально.

Решение матриц в Excel

С матрицами в Excel производятся такие операции, как: транспонирование, сложение, умножение на число / матрицу; нахождение оборотной матрицы и ее определителя.

Транспонирование

Транспонировать матрицу – поменять строчки и столбцы местами.

Поначалу отметим пустой спектр, куда будем транспонировать матрицу. В начальной матрице 4 строчки – в спектре для транспонирования обязано быть 4 столбца. 5 колонок – это 5 строк в пустой области.

1 метод. Выделить начальную матрицу. Надавить «копировать». Выделить пустой спектр. «Развернуть» кнопку «Вставить». Открыть меню «Специальной вставки». Отметить операцию «Транспонировать». Закрыть диалоговое окно нажатием клавиши ОК.
2 метод. Выделить ячейку в левом верхнем углу пустого спектра. Вызвать «Мастер функций». Функция ТРАНСП. Аргумент – спектр с начальной матрицей.

Жмем ОК. Пока функция выдает ошибку. Выделяем весь спектр, куда необходимо транспонировать матрицу. Жмем клавишу F2 (перебегаем в режим редактирования формулы). Жмем сочетание кнопок Ctrl + Shift + Enter.

Преимущество второго метода: при внесении конфигураций в начальную матрицу автоматом изменяется транспонированная матрица.

Сложение

Ложить можно матрицы с схожим количеством частей. Число строк и столбцов первого спектра обязано приравниваться числу строк и столбцов второго спектра.

В первой ячейке результирующей матрицы необходимо ввести формулу вида: = 1-ый элемент первой матрицы + 1-ый элемент 2-ой: (=B2+H2). Надавить Enter и растянуть формулу на весь спектр.

Умножение матриц в Excel

Чтоб помножить матрицу на число, необходимо любой ее элемент помножить на это число. Формула в Excel: =A1*$E$3 (ссылка на ячейку с числом обязана быть абсолютной).

Умножим матрицу на матрицу различных диапазонов. Отыскать произведение матриц можно лишь в том случае, если число столбцов первой матрицы приравнивается числу строк 2-ой.

В результирующей матрице количество строк приравнивается числу строк первой матрицы, а количество колонок – числу столбцов 2-ой.

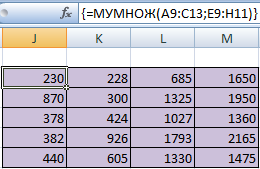
Для удобства выделяем спектр, куда будут помещены результаты умножения. Делаем активной первую ячейку результирующего поля. Вводим формулу: =МУМНОЖ(A9:C13;E9:H11). Вводим как формулу массива.

Оборотная матрица в Excel

Ее имеет смысл отыскивать, если мы имеем дело с квадратной матрицей (количество строк и столбцов однообразное).

Размерность оборотной матрицы соответствует размеру начальной. Функция Excel – МОБР.

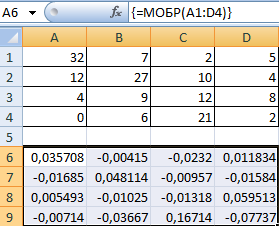
Выделяем первую ячейку пока пустого спектра для оборотной матрицы. Вводим формулу «=МОБР(A1:D4)» как функцию массива. Единственный аргумент – спектр с начальной матрицей. Мы получили оборотную матрицу в Excel:

Нахождение определителя матрицы

Это одно единственное число, которое находится для квадратной матрицы. Применяемая функция – МОПРЕД.

Ставим курсор в хоть какой ячейке открытого листа. Вводим формулу: =МОПРЕД(A1:D4).

Таковым образом, мы произвели деяния с матрицами при помощи интегрированных способностей Excel.

Знакомство с матрицами

Создатели нейросетей молвят, что все нейросети — это просто нескончаемое перемножение матриц. Мы решили разобраться, что же это все-таки за матрицы и как их перемножать, а для этого пришлось полезть в линейную алгебру. И это оказалось не так трудно, как мы задумывались:

У вектора быть может снутри сколько угодно чисел. Основное — чтоб мы условились, что для нас значат эти числа, и не меняли их местами просто так, произвольно.
Векторы можно ложить, вычитать, множить. Это чуток труднее, чем с обыкновенными числами.
У вектора есть понятие линейной зависимости. Грубо говоря — параллельны друг дружке векторы либо нет. От этого зависит, какие операции можно созодать с этими векторами.

Вектор — это «кирпичик» линейной алгебры. На его базе мы перебегаем к понятию матрицы.

Что такое матрица

Если вектор — это строчка с числами в определённом порядке, то матрица — это таблица с числами в определённом порядке. Как у хоть какой таблицы, у матрицы есть столбцы и строчки. В их посиживают какие-то числа. Всё совместно — это математический объект, другими словами в каких-либо вариантах всю эту таблицу можно разглядывать как единое целое и совершать с ним операции.

Матрицы принято обозначать большенными знаками латинского алфавита вроде А, В, С, D и так дальше.

Числа снутри матрицы именуют элементами. Любой элемент обозначается 2-мя цифрами: 1-ая цифра показывает на строчку, а 2-ая — на столбец. Это адресок числа снутри матрицы. К примеру, элемент А₂₃ значит, что необходимое число находится во 2-ой строке и 3-ем столбце. Нумерация частей нужна для записи формул и устного разъяснения того, где находится необходимое число в матрице.

В матрице может находиться огромное количество строк, столбцов и частей. Из-за этого матрицы бывают различных видов и могут владеть различными чертами. К примеру, если в матрице совпадает число строк и столбцов, то таковая матрица именуется квадратной.

В данной для нас статье и в последующих материалах мы будем разглядывать различные виды матрицы и равномерно изучим их индивидуальности.

Общая схема матрицы Пример квадратной матрицы с пятью строчками и столбцами. Записывается как матрица размера 5×5. В числовой матрице мы не нумеруем элементы — они закрепляются за числами по дефлоту. К примеру, элементу А₂₃ соответствует число три

Обыкновенные операции с матрицами

Вынесение минуса за границы матрицы. Если снутри матрицы у большинства частей символ минус, то нередко это мешает расчётам либо приводит к ошибкам. Чтоб этого избежать, от минуса избавляются. Для этого необходимо вынести минус за границы матрицы и поменять символ всех частей снутри самой матрицы.

И напротив: если снутри матрицы у большинства частей символ минус и перед матрицей стоит минус, то минус можно внести в матрицу.

Выносим минус за границы матрицы и получаем заместо 20 1-го отрицательного элемента — четыре Перед матрицей минус, и снутри у большинства частей минус. Вносим минус в матрицу и делаем её комфортной для последующих вычислений

Умножение матрицы на число. Для умножения матрицы на число довольно любой элемент матрицы помножить на это число.

Интересно почитать: Excel несколько файлов объединить в один

Пример умножения матрицы на число

Транспонирование матрицы. Это операция, которая позднее нам пригодится для решения матричных уравнений. Для транспонирования мы берём известную матрицу, меняем в ней местами строчки со столбцами и получаем новейшую матрицу. Вроде бы поставили матрицу набок.

⚠️ При всем этом в матрице запрещено в случайном порядке поменять элементы. Зато можно стопроцентно поменять местами строчки либо столбцы. Если мы поменяем местами первую и вторую строчку, то это остается прежняя матрица.

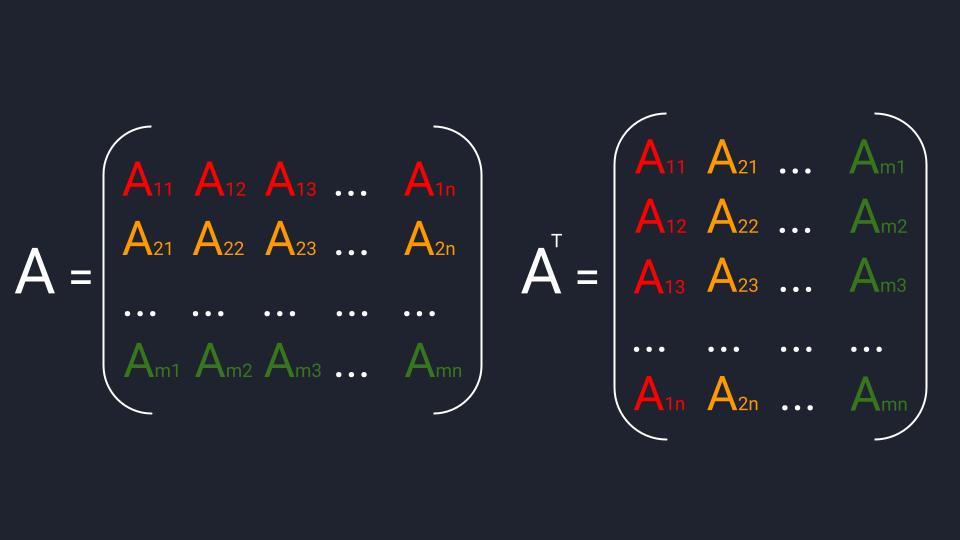Схема транспонирования матриц: 1-ая строчка перебегает в 1-ый столбец, 2-ая строчка — во 2-ой столбец и так дальше в зависимости от количества частей матрицы Пример транспонирования. Транспонированная матрица обозначается буковкой той же матрицы, из которой она вышла + надстрочечный индекс в виде печатной буковкы «Т» 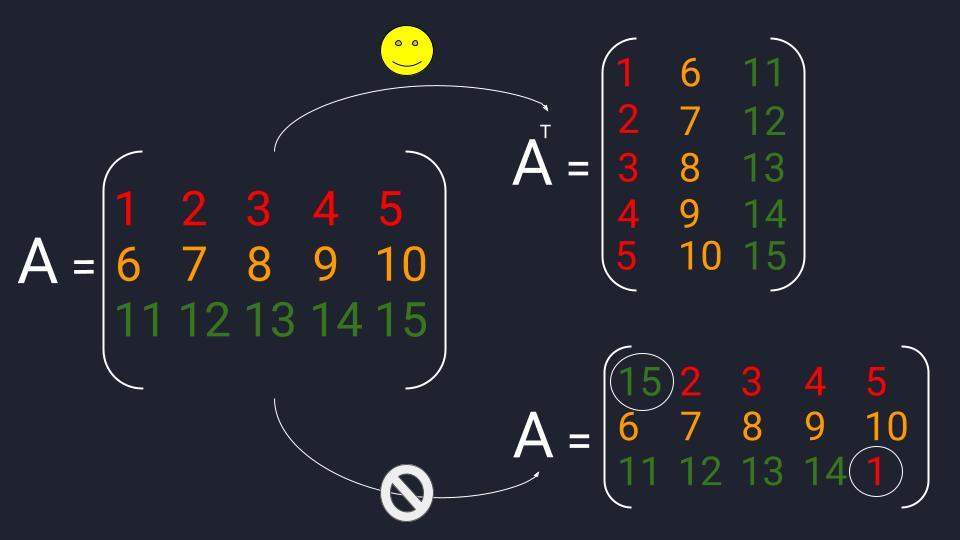Матрицу можно перетасовывать, но это необходимо созодать по правилам. Транспонирование — одно из таковых правил

Сложение и вычитание матриц

Если в нескольких матрицах совпадает число строк и столбцов, то мы можем их ложить и вычитать. Для вычислений нам необходимо поэлементно сложить либо отнять любой элемент матриц: 1-ый элемент первой матрицы складываем с первым элементом 2-ой матрицы либо вычитаем из него и так дальше. В итоге получаем новейшую матрицу.

Пример сложения 2-ух прямоугольных матриц с 3-мя строчками и 2-мя столбцами Пример вычитания 2-ух матриц

Умножение матриц

Матрицы множатся по принципу строчка на столбец. Мы умножаем первую строчку первой матрицы, на 1-ый столбец 2-ой матрицы, складываем результаты и получаем 1-ый элемент новейшей матрицы. По аналогичной схеме вычисляем все другие элементы. Звучит запутанно, потому идём по шагам:

У нас есть две матрицы A и B. Их необходимо перемножить, чтоб получить новейшую матрицу C.
Размер матрицы A два на два: есть две строчки и два столбца. 1-ая строчка состоит из частей А₁₁ и А₁₂; 2-ая — А₂₁ и А₂₂.
У матрицы B таковая же размерность: есть две строчки и два столбца. 1-ая строчка состоит из частей B₁₁ и B₁₂; 2-ая — B₂₁ и B₂₂.
У нас две схожие по размеру матрицы с 2-мя строчками и столбцами. Это означает, что и матрица C будет размером два на два. 1-ая строчка будет состоять из частей C₁₁ и C₁₂; 2-ая — C₂₁ и C₂₂.
Считаем элемент C₁₁. Умножаем 1-ый элемент первой строчки матрицы А (А₁₁) на 1-ый элемент первого столбика матрицы B (B₁₁). Это 1-ая часть, опосля которой ставим символ плюс. 2-ая часть: умножаем 2-ой элемент первой строки матрицы А (А₁₂) на 2-ой элемент первого столбика матрицы B (B₂₁). Складываем обе части и получаем 1-ый элемент первой строчки матрицы С (C₁₁).
Считаем элемент C₁₂. Умножаем 1-ый элемент первой строчки матрицы А (А₁₁) на 1-ый элемент второго столбика матрицы B (B₁₂). Это 1-ая часть. 2-ая часть: умножаем 2-ой элемент первой строки матрицы А (А₁₂) на 2-ой элемент второго столбика матрицы B (B₂₂). Складываем части и получаем 2-ой элемент первой строчки матрицы С (C₁₂).
Считаем элемент C₂₁. Умножаем 1-ый элемент 2-ой строчки матрицы А (А₂₁) на 1-ый элемент первого столбика матрицы B (B₁₁). Это 1-ая часть. 2-ая часть: умножаем 2-ой элемент 2-ой строчки матрицы А (А₂₂) на 2-ой элемент первого столбика матрицы B (B₂₁). Складываем части и получаем 1-ый элемент 2-ой строчки матрицы С (C₂₁).
Считаем элемент C₂₂. Умножаем 1-ый элемент 2-ой строчки матрицы А (А₂₁) на 1-ый элемент второго столбика матрицы B (B₁₂). Это 1-ая часть. 2-ая часть: умножаем 2-ой элемент 2-ой строчки матрицы А (А₂₂) на 2-ой элемент второго столбика матрицы B (B₂₂). Складываем части и получаем 2-ой элемент 2-ой строчки матрицы С (C₂₂).

Если нам необходимо отыскать матрицу в квадрате, то мы умножаем эту матрицу на саму себя. Если нужна матрица в кубе — умножаем её на саму себя трижды и так дальше в зависимости от количества степеней. Если в одной из матриц все элементы нули, то она считается нулевой и опосля умножения на другую матрицу даёт нулевую матрицу — это как нуль умноженный на число постоянно даёт нуль.

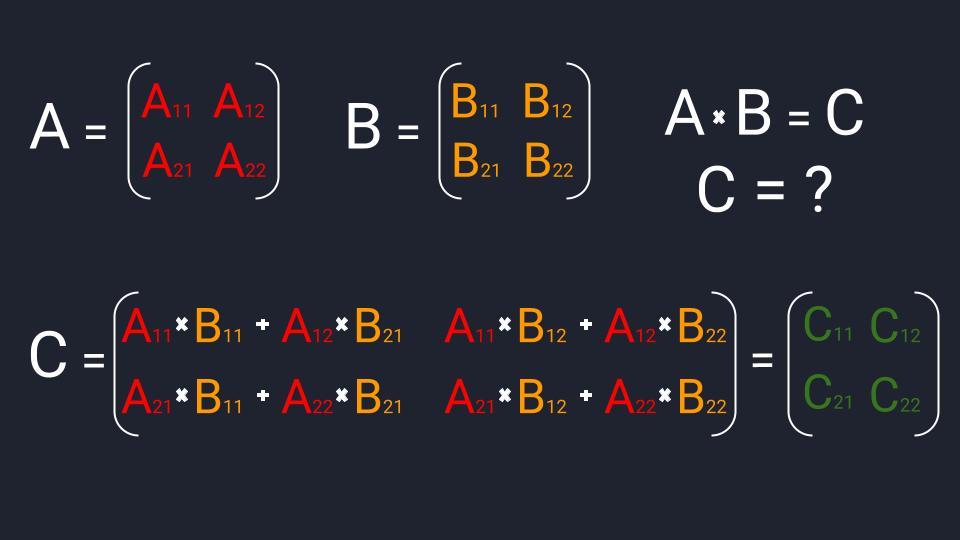Формула умножения матриц Пример умножения квадратных матриц размерностью 2×2

Что далее

В последующий раз продолжим знакомиться с базисными понятиями, которые нам пригодятся для решения матричных уравнений. А на сей день Нео волен

Три метода умножения матриц в Excel — fastai part-2, lesson-8

Часть-2 изФастай «Из фондов»наконец вышел. Я не помню, когда в крайний раз я был так взволнован по поводу MOOC. Как курс был обнародован, я начал копаться в нем, чтоб углубить свое осознание глубочайшего обучения и основополагающих концепций.

Сейчас я решил последовать совету Джереми и Рэйчел и написать блоги. Эта определенная статья разъясняетразные способы умножения матриц,что Джереми реализует в Уроке-8. Я буду применятьМайкрософт Эксельдля иллюстрации.

Умножение матриц

Хорошее и интерактивное пространство для осознания умножения матриц, на которое ссылается Джереми, доступно по адресу:

На самом деле, как видно из изображения, мы берем транспонирование 2-ой матрицы, умножаем и складываем элементы совместно, чтоб получить итог. Как пример, самый 1-ый пункт 15 в результирующей матрице происходит от 1*2 + 6*2 + 1*1 = 2 + 12 + 1 = 15 ,

Хотя это разъяснение зрительно приятно, по моему умеренному воззрению, его тяжело конвертировать в код. Так что давайте применять Excel и осознавать матричное умножение по-другому!

Умножение матриц в EXCEL

Разглядим две матрицы такжеВразмера 4×3 также 3×4 ,
Примечание: я буду применять жирный шрифт такжеВсослаться на матрицы в данной для нас статье. Рядовая практика — ссылаться на векторы и матрицы, используя жирный шрифт.

Из изображения, которое мы лицезрели ранее, если вы помните, мы взяли транспонированиеВи умноженные строчки с колоннамиВчтоб получить результирующую матрицу. Быстрее, давайте пропустим этот шаг, сделав транспонирование сейчас, и сходу умножим строчки и столбцы.

Потому строчка 0 из множится на столбец 0Впоэлементные и результирующие поэлементные продукты добавляются для получения первого элемента в результирующей матрицеСв положении [0][0] ,

Ах так это смотрится в Excel:

Буквально так же мы получаем C[0][3] поэлементно умножая строчку 0 из и кол 3 изB.В Excel это смотрится так:

Интересно почитать: Excel доступ к файлу невозможен проверьте следующее

И, в конце концов, мы следуем тому же процессу, чтоб пройти любой пустой ящик вСчтоб получить окончательный итог.

Вот и мы! Вот так мы делаем матричное умножение! Это было просто, не так ли? Мы сейчас не только лишь сообразили умножение матриц, да и ввели его в Excel! Как это круто?

Я лично считаю, что сейчас вы готовы работать с некими правилами, связанными с умножением матрицMatMul):

Позволять ar,ac быть количеством строк и столбцов вA.Буквально так же, пусть br, bc быть количеством строк и столбцов вB.Тогда для выполнения умножения матриц нужно, чтоб ac == br , Для чего? Итак, как вы лицезрели в Excel, мы помножили строчки и столбцы поэлементно, а потом добавили промежные продукты, чтоб получить конечный итог. Если есть несоответствие в размерах, и один вектор длиннее другого, мы больше не можем делать поэлементное умножение!
Размеры результирующей матрицы постоянно будут ar,bc , Другими словами количество строк исходит от и количество столбцов исходит отB.

Метод 1: внедрение 3-х циклов FOR

Вот очередной отказ от ответственности, при реализации умножения матриц в Excel, мы не только лишь сообразили это, да и повторили 1-ый способ Джереми, который употреблял 3 цикла FOR. Ах так это смотрится в коде:

Надеюсь, сейчас вы можете лучше осознать это. Если нет, то на данный момент самое время создать паузу, поэкспериментировать с кодом и поглядеть, что по сути происходит. Я обещаю для вас, это так же, как наша версия Excel!

Отлично, я предполагаю, что вы издержали некое время на размышления о коде, потому давайте обсудим это!

Почему 1-ые две петли в range(ar) также range(bc) ? Ну, как вы помните изПравило-2наша результирующая матрица будет иметь размеры ar,bc , И из Excel мы узрели, что мы пересекаем любой элементСкак следует, один за остальным, чтоб пройти ar строчки и bc столбцы нам необходимо 2 цикла в range(ar) также range(bc) ,
Итак, почему 3-ий цикл FOR в range(ac) #or br ? Ну изПравило-1, мы знаем это ac==br так что по сути не имеет значения, ставим ли мы range(ac) либо range(br) в 3-ем цикле. На самом деле, конкретно тут отдельные элементы множатся совместно и добавляются. Из нашего предшествующего примера Excel, для C[0][0] это где шаг C[0][0] = 1*1 + 10*5 + 100*9 = 1 + 50 + 900 = 951 произойдет, и, в конце концов, мы перейдем к последующей коробке. Количество предметов, которые множатся и складываются совместно, равно ac or br ,

Это вправду так! Это метод-1 вам! Вот песня, чтоб держать в голове Матричное Умножение. (Я вызнал о этом первым из fast.ai, уникальный создатель неизвестен)

Надеюсь, сейчас вы осознаете, как две матрицы множатся друг на друга. Если не,Вотэто очередной учебник Хан Академии

Способ 2: Внедрение поэлементного умножения

Так что до сего времени мы разбираем каждую позицию в результирующей матрицеC,отыскать отдельные элементы, а потом суммировать их совместно. Если вы помните, что-то вроде C[0][0] = 1*1 + 10*5 + 100*9 = 1 + 50 + 900 = 951 , Естественно, должен быть иной путь? Что если заместо того, чтоб созодать отдельные продукты, а потом суммировать их, мы умножаем векторы за один раз, чтоб получить результирующий вектор, и суммируем приобретенный вектор, чтоб получить конечный элемент?

До сего времени мы находили отдельные продукты 10, 20, 30 и сложить их совместно 10 + 20 + 30 = 60 , Но, вправду, все это можно поменять на:

Если вы помните, самый внутренний цикл в range(ac) #or br находил отдельные продукты и добавлял их. Ну, мы можем поменять этот цикл, чтоб выполнить векторное поэлементное произведение и положить .sum() в конце концов, и PyTorch / NumPy имеют возможность делать поэлементные операции для нас!

Ах так это смотрится в Excel:

Буквально так же мы получаем C[0][3] методом умножения вектора в строке 0 с вектором на цв 3Ви суммируя приобретенный вектор.

Направьте внимание, как это различается отСпособ-1? Сейчас мы просто говорим Excel либо PyTorch: помножьте строчку 0 с col 0 изВи суммируем приобретенный вектор, чтоб отдать нам ответ. Заместо того чтоб созодать 1*1 + 10*5 + 100*9 , К примеру, для C[0][0] этот способ множит Vector на строчку 0 tensor([1,10,100]) с вектором в столбце 0 изВ tensor<[1,5,9]) чтоб получить промежный продукт Вектор tensor([1,50,900]) и суммирует это, чтоб отдать итог в положении C[0][0] как tensor(951) ,

В коде это смотрится так:

Таковым образом, мы просто анализируем каждую позициюC,используя две петли FOR и введите соответственный итог в данной для нас позиции. Если i,j представляют строчки и столбцы вСэто смотрится приблизительно так .

И так дальше .. пока мы не получим полную матрицуС,

Способ 3: вещание

Увидели общую тему тут? Всякий раз мы должны помножить любой ряд с каждым столбцомВполучитьС, Вы замечаете повторение? Мы умножаем один и этот же вектор строчки в bc раз! И мы повторяем этот процесс ar раз!

Есть ли метод помножить вектор строчки со всеми столбцамиВполучить соответственный ряд вC?Да, есть! Войдите в трансляцию .
Примечание: я не буду разъяснять вещание, Джереми делает это весьма хорошоВот,

Заместо этого давайте поглядим, что же это все-таки за магический кусочек кода

Как обычно, давайте повторим в Excel! Это сделает вещи вправду легкими. Давайте создадим это поэтапно.

Шаг 1)Изберите i-й ряд a[i,:] , Мы избираем строчку 0 в качестве примера.