Как транспонировать матрицу в Python
Сейчас мы желаем разобрать, как транспонировать матрицу в Python. Но поначалу давайте разглядим, что представляет из себя матрица сама по для себя и в чём заключается процесс транспонирования.
Итак, матрица состоит из строк и столбцов. Сделать матрицу можно по-разному, но самый обычной метод – применять вложенные списки, как показано ниже:
Внутренние списки представляют собой строчки, а любой элемент снутри перечня именуется столбцом. Итак, в приведенном выше примере у нас есть две строчки и три столбца, т.е. мы имеем дело с матрицей 2 на 3. Стоит держать в голове, что индексация Python начинается с нуля.
Транспонирование матрицы значит, что мы меняем строчки на столбцы либо столбцы на строчки. Сейчас давайте обсудим разные способы транспонирования матрицы.
Способ 1. Транспонирование матрицы при помощи NumPy transpose()
1-ый способ, который мы разберем, — это внедрение библиотеки NumPy. NumPy в основном работает с массивами в Python, а для транспонирования мы можем вызвать способ transpose() .
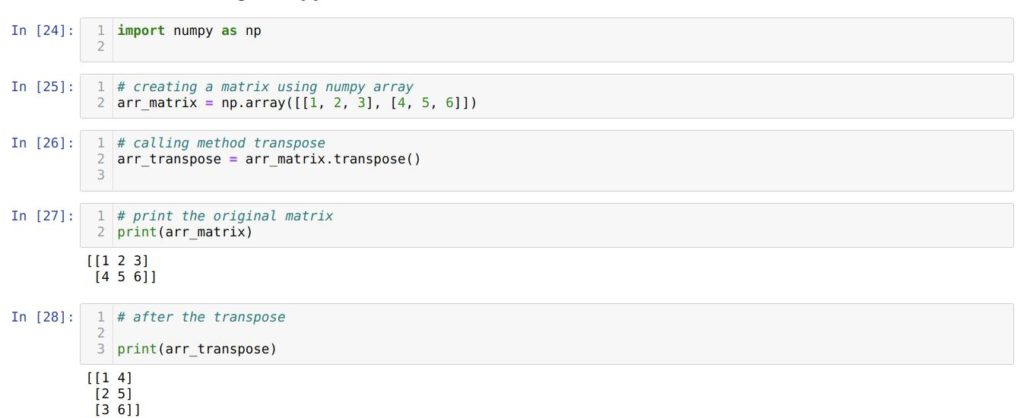
Давайте разберем всё по порядку. Для начала нам необходимо импортировать модуль NumPy как np .
Далее, в ячейке номер [25] мы создаем массив NumPy с именованием arr_matrix .
В ячейке номер [26] мы вызываем способ transpose() для нашей матрицы – объекта arr_matrix , который мы сделали ранее.
В ячейке номер [27] мы выводим на экран начальную матрицу arr_matrix .
А в ячейке номер [28] – транспонированную матрицу arr_transpose . Можем увидеть, что в итоге мы получили конкретно то, что нам было необходимо – транспонированную матрицу.
Способ 2. Внедрение способа numpy.transpose()
Мы также можем транспонировать матрицу в Python при помощи numpy.transpose() . При всем этом мы передаем матрицу в способ transpose() в качестве аргумента.
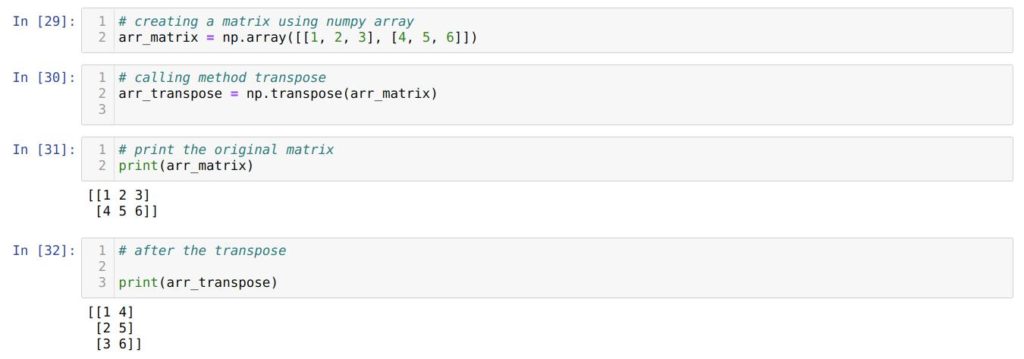
В ячейке номер [29] мы создаем матрицу, используя массив NumPy, с именованием arr_matrix .
Дальше мы передаем arr_matrix в способ transpose() и сохраняем итог в новейшую переменную arr_transpose .
В ячейке номер [31] мы печатаем начальную матрицу arr_matrix .
А далее мы выводим на экран транспонированную матрицу arr_transpose . Получаем итог аналогичный тому, что получили в первом примере.
Способ 3. Транспонирование матрицы с внедрением библиотеки SymPy
Применение библиотеки SymPy – это очередной подход к транспонированию матрицы. Эта библиотека употребляет символьную арифметику для решения алгебраических задач.
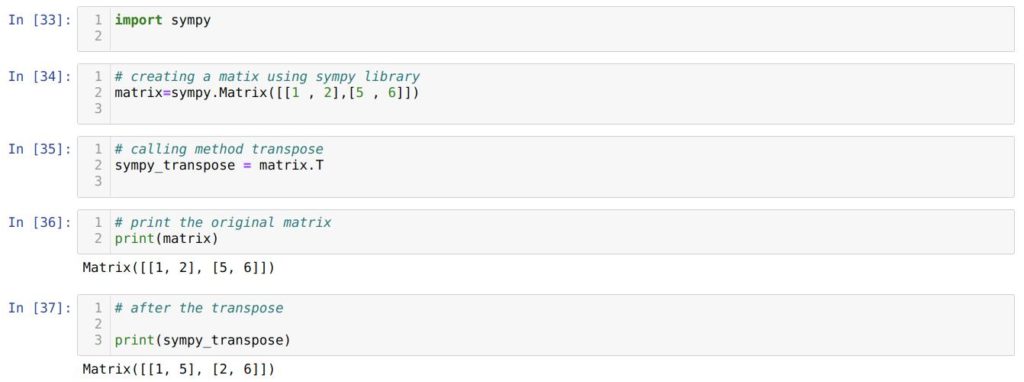
Поначалу нам, естественно же, необходимо импортировать библиотеку SymPy. Она не поставляется совместно с Python по дефлоту, потому вы должны установить её в собственной системе, по другому код не будет работать.
В ячейке номер [34] мы создаем матрицу при помощи библиотеки sympy.
Далее, в ячейке [35], мы вызываем transpose (T) с помощью точечного оператора и сохраняем результаты в новейшую переменную sympy_transpose .
В ячейке номер [36] мы печатаем начальную матрицу matrix . А в ячейке номер [37] – транспонированную матрицу sympy_transpose . Как лицезреем, у нас вышла транспонированная матрица.
Способ 4. Транспонирование матрицы с внедрением вложенного цикла
В Python матрицу можно транспонировать и без внедрения каких-то библиотек. Для этого нам придется применять вложенные циклы.
Мы создаем одну матрицу, а потом вторую (такого же размера, что и 1-ая) — для сохранения результатов опосля транспонирования. При всем этом принципиально отметить, что мы далековато не постоянно знаем размерность начальной матрицы. Потому матрицу для результата мы создаем не впрямую, а используя размер начальной.
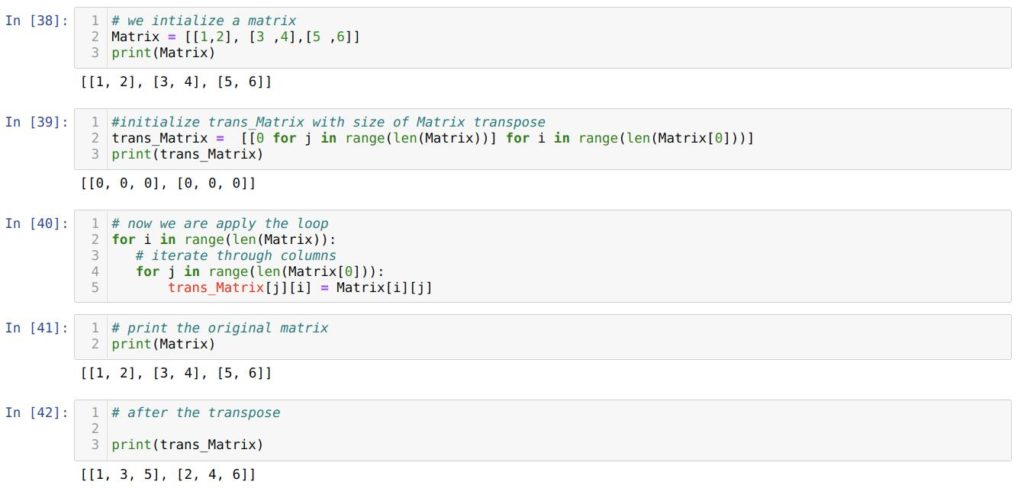
В ячейке номер [38] мы создаем матрицу и выводим ее на экран.
В последующей ячейке мы применяем «питонический» метод выяснить размерность транспонированной матрицы, используя начальную. А конкретно — используем генератор списков со вложенными циклами for .
В ячейке [40] мы запускаем два цикла for . Наружный цикл предназначен для строк, а вложенный – для столбцов.
В ячейке номер [41] мы выводим начальную матрицу Matrix . А в ячейке [42] — транспонированную матрицу trans_Matrix .
Способ 5. Внедрение генератора перечня
Последующий способ, который мы разберем, — это внедрение генератора перечня. Этот способ похож на предшествующий с внедрением вложенных циклов, но он наиболее «питонический». Можно сказать, что это наиболее продвинутый метод транспонирования матрицы в одной строке кода без использования библиотек.
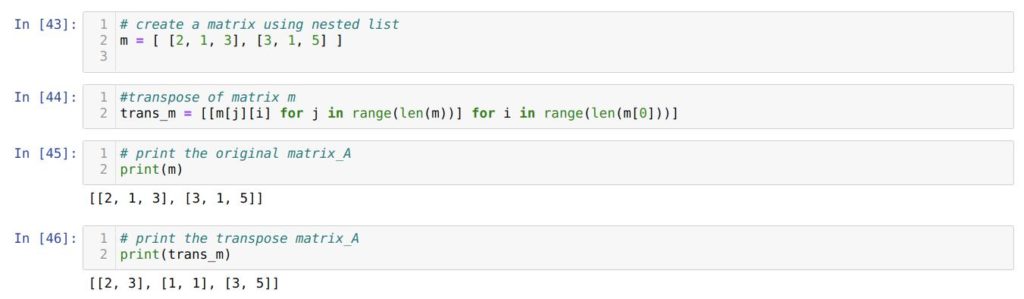
Поначалу мы создаем матрицу m , используя вложенные списки.
Потом в ячейке номер [44] мы используем вложенные циклы, как и в прошлом примере. Но тут мы делаем это в одну строку, используя генератор списков. Наиболее того, здесь нет никакой необходимости поменять индексы [j] [i] местами, как мы это делали в предшествующий раз.
В последующей ячейке мы выводим начальную матрицу m . Опосля этого в ячейке номер [42] выводим транспонированную матрицу trans_m . Как лицезреем, хотимый итог получен.
Способ 6. Транспонирование матрицы при помощи pymatrix
Pymatrix – ещё одна облегченная библиотека для матричных операций в Python. Мы можем выполнить транспонирование и с её помощью.
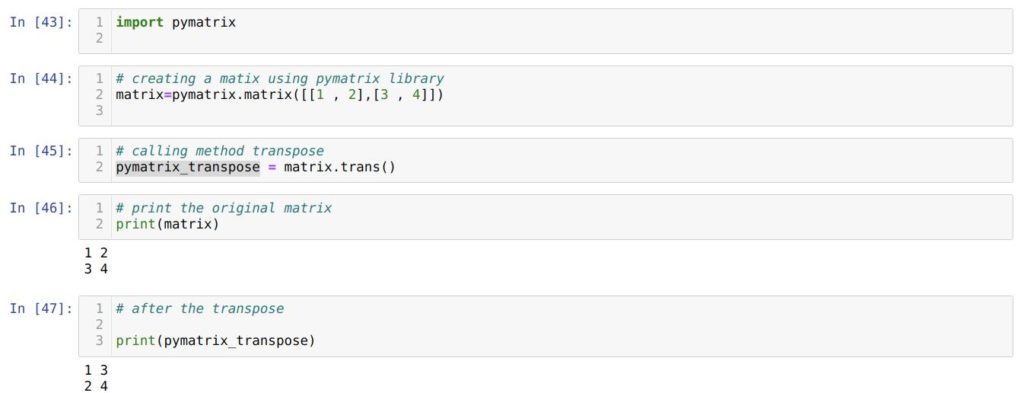
В ячейке номер [43] мы импортируем библиотеку pymatrix. Она не поставляется совместно с Python по дефлоту, потому, чтоб код работал корректно, необходимо установить ее в собственной системе перед внедрением.
Потом с помощью библиотеки pymatrix мы создаем матрицу (в ячейке [44]).
В ячейке номер [45] вызываем способ trans() для нашей матрицы и сохраняем результаты в новейшую переменную pymatrix_transpose.
Позже мы выводим на экран начальную матрицу matrix . А в ячейке номер [47] выводим уже транспонированную матрицу pymatrix_transpose . Как лицезреем, код отработал верно.
Способ 7. Внедрение способа zip
Zip – очередной способ транспонирования матрицы.
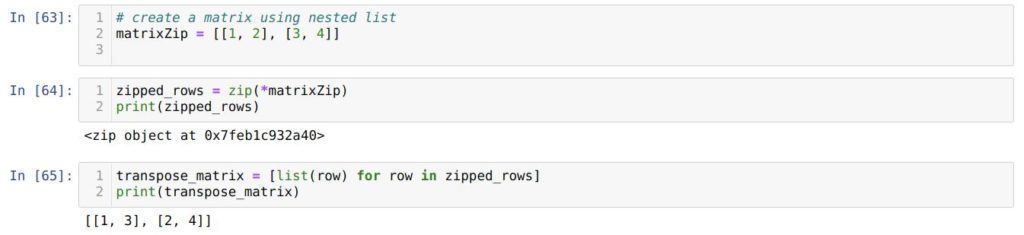
В ячейке номер [63] мы создаем новейшую матрицу, используя вложенные списки.
В ячейке номер [64] мы передаем матрицу в zip при помощи оператора * . Мы вызываем каждую строчку, а потом преобразуем эту строчку в новейший перечень, который становится транспонированной матрицей.
Заключение
Итак, сейчас мы разглядели, как транспонировать матрицу в Python. Мы разобрали разные способы, которые могут посодействовать нам в транспонировании матрицы (с внедрением библиотек и без их).
Мы также познакомились с несколькими новенькими библиотеками, таковыми как pymatrix и sympy.
Возлагаем надежды, сейчас у вас не осталось вопросцев о том, как транспонировать матрицу. Наиболее того, вы сможете избрать более пригодный метод для решения данной задачки.