Как высчитать дисперсию в Excel
Итак, вас попросили высчитать дисперсию при помощи Excel, но вы не понимаете, что это значит и как это создать. Не беспокойтесь, это обычная теория и еще наиболее обычный процесс. Вы станете специалистом в дисперсии в кратчайшие сроки!
Что такое дисперсия?
«Дисперсия» — это метод измерения среднего расстояния от среднего. «Среднее» — это сумма всех значений в наборе данных, деленная на количество значений. Дисперсия дает нам представление о том, имеют ли значения в этом наборе данных тенденцию в среднем умеренно придерживаться среднего значения либо разбросаны всюду.

Математически дисперсия не так сложна:
- Вычислите среднее значение набора значений. Чтоб вычислить среднее значение, возьмите сумму всех значений, разбитую на количество значений.
- Возьмите каждое значение в вашем наборе и вычтите его из среднего.
- Возведите приобретенные значения в квадрат (чтоб исключить отрицательные числа).
- Сложите все квадраты значений совместно.
- Вычислите среднее квадратов значений, чтоб получить дисперсию.
Видите ли, вычислить это значение нетрудно. Но если у вас есть сотки либо тыщи значений, на то, чтоб создать это вручную, уйдет целая вечность. Так что отлично, что Excel может заавтоматизировать этот процесс!
Для что вы используете дисперсию?
Сама по для себя дисперсия имеет ряд применений. С чисто статистической точки зрения это неплохой метод обозначить, как разрознен набор данных. Инвесторы употребляют дисперсию для оценки риска данной инвестиции.
К примеру, взяв стоимость акции за определенный период времени и вычислив ее дисперсию, вы получите не плохое представление о ее волатильности в прошедшем. Если представить, что прошедшее предвещает будущее, это будет означать, что что-то с низкой дисперсией наиболее неопасно и прогнозируемо.

Вы также сможете сопоставить отличия чего-либо в различные периоды времени. Это может посодействовать найти, когда иной сокрытый фактор на что-то влияет, изменяя его дисперсию.
Дисперсия также очень связана с иной статистикой, известной как обычное отклонение. Помните, что значения, применяемые для расчета дисперсии, возведены в квадрат. Это значит, что отклонение не выражается в той же единице начального значения. Обычное отклонение просит извлечения квадратного корня из дисперсии, чтоб возвратить значение в начальную единицу. Таковым образом, если данные были в килограммах, обычное отклонение тоже.
Выбор меж совокупой и дисперсией подборки
В Excel есть два подтипа дисперсии с незначительно различными формулами. Какой из их избрать, зависит от ваших данных. Если ваши данные включают всю «генеральную совокупа», для вас следует употреблять дисперсию генеральной совокупы. В этом случае «популяция» значит, что у вас все есть значения для всякого члена мотивированной группы населения.

К примеру, если вы поглядите на вес левшей, то в популяцию войдут все левши на Земле. Если вы их все взвесите, вы воспользуетесь дисперсией населения.
Естественно, в настоящей жизни мы обычно соглашаемся на наименьшую подборку из большей совокупы. В этом случае вы должны употреблять выборочную дисперсию. Дисперсия совокупы как и раньше животрепещуща для маленьких популяций. К примеру, в компании быть может несколько сотен либо несколько тыщ служащих с данными о любом сотруднике. Они представляют собой «население» в статистическом смысле.
Выбор правильной формулы дисперсии
В Excel есть три типовых формулы дисперсии и три формулы дисперсии генеральной совокупы:
- VAR, VAR.S и VARA для выборочной дисперсии.
- VARP, VAR.P и VARPA для дисперсии совокупы.
Вы сможете игнорировать VAR и VARP. Они устарели и есть лишь для сопоставимости с устаревшими электрическими таблицами.
Остается VAR.S и VAR.P, которые предусмотрены для вычисления дисперсии набора числовых значений, также VARA и VARPA, которые включают текстовые строчки.

VARA и VARPA конвертируют всякую текстовую строчку в числовое значение 0, кроме «ИСТИНА» и «ЛОЖЬ». Они преобразуются в 1 и 0 соответственно.
Наибольшая разница в том, что VAR.S и VAR.P пропускают любые нечисловые значения. Это исключает эти случаи из полного количества значений, что значит, что среднее значение будет иным, поэтому что вы делите на наименьшее количество случаев, чтоб получить среднее значение.
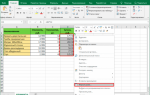
Все, что для вас необходимо для расчета дисперсии в Excel, — это набор значений. Мы собираемся употреблять VAR.S в приведенном ниже примере, но формула и способы буквально такие же, независимо от того, какую формулу дисперсии вы используете:
- Предполагая, что у вас есть готовый спектр либо дискретный набор значений, изберите пустую ячейку по вашему выбору.

- В поле формулы введите = VAR.S (XX: YY), где значения X и Y заменяются номерами первой и крайней ячеек спектра.

- Нажмите Enter, чтоб окончить расчет.

В качестве кандидатуры вы сможете указать определенные значения, и в этом случае формула будет иметь вид = VAR.S (1,2,3,4). С числами, замененными на все, что для вас необходимо для расчета дисперсии. Вы сможете ввести до 254 значений вручную таковым образом, но если у вас есть лишь несколько значений, практически постоянно лучше вводить данные в спектре ячеек, а потом употреблять версию формулы, описанную выше, для спектра ячеек.
Вы сможете Excel в, Er, Excel
Вычисление дисперсии — нужный прием для тех, кому необходимо выполнить статистическую работу в Excel. Но если какая-либо терминология Excel, которую мы употребляли в данной статье, сбивала с толку, задумайтесь о том, чтоб ознакомиться с Управлением по основам Microsoft Excel — Обучение (педагогический процесс, в результате которого учащиеся под руководством учителя овладевают знаниями, умениями и навыками) использованию Excel.
Если, с иной стороны, вы готовы к большему, ознакомьтесь с разделом «Добавить линию тренда линейной регрессии на точечную диаграмму Excel», чтоб вы могли визуализировать дисперсию либо хоть какой иной нюанс вашего набора данных по отношению к среднему арифметическому.