Сложные проценты в EXCEL. Неизменная ставка
Обладатель капитала, предоставляя его на определенное время в долг, рассчитывает на получение дохода от данной нам сделки. Размер ожидаемого дохода зависит от 3-х причин: от величины капитала, предоставляемого в кредит, от срока, на который предоставлен кредит, и от величины ссудного процента либо по другому процентной ставки.
Есть разные способы начисления процентов. Основное их различие сводится к определению начальной суммы (базы), на которую начисляются проценты. Эта сумма может оставаться неизменной в течение всего периода либо изменяться. Зависимо от этого различают способ начисления по обычным и сложным процентам.
При использовании сложных ставок процентов процентные средства, начисленные опосля всякого периода начисления, присоединяются к сумме долга. Таковым образом, база для начисления сложных процентов в отличие от использования обычных процентов меняется в любом периоде начисления. Присоединение начисленных процентов к сумме, которая послужила базой для их начисления, именуется капитализацией процентов. Время от времени этот способ именуют «процент на процент».
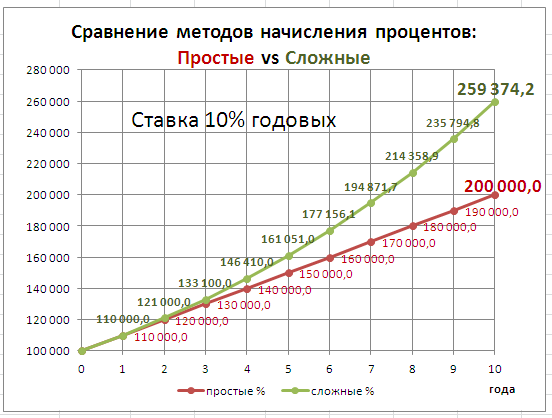
В файле примера приведен график для сопоставления наращенной суммы с внедрением обычных и сложных процентов.
В данной нам статье разглядим начисление по сложным процентам в случае неизменной ставки. О переменной ставке в случае сложных процентов читайте тут .
Начисление процентов 1 раз в год
Пусть начальная сумма вклада равна Р, тогда через один год сумма вклада с присоединенными процентами составит =Р*(1+i), через 2 года =P*(1+i)*(1+i)=P*(1+i)^2, через n лет – P*(1+i)^n. Таковым образом, получим формулу наращения для сложных процентов: S = Р*(1+i)^n где S — наращенная сумма, i — годичная ставка, n — срок ссуды в годах, (1+ i)^n — множитель наращения.
Начисление процентов пару раз в год
В рассмотренном выше случае капитализация делается 1 раз в год. При капитализации m раз в год формула наращения для сложных процентов смотрится так: S = Р*(1+i/m)^(n*m) i/m – это ставка за период. На практике обычно употребляют дискретные проценты (проценты, начисляемые за схожие интервалы времени: год (m=1), полугодие (m=2), квартал (m=4), месяц (m=12)).
В MS EXCEL вычислить наращенную сумму к концу срока вклада по сложным процентам можно различными методами.
Разглядим задачку : Пусть начальная сумма вклада равна 20т.р., годичная ставка = 15%, срок вклада 12 мес. Капитализация делается каждый месяц в конце периода.
Метод 1. Вычисление при помощи таблицы с формулами Это самый трудозатратный метод, но зато самый приятный. Он заключается в том, чтоб поочередно вычислить величину вклада на конец всякого периода. В файле примера это реализовано на листе Неизменная ставка .
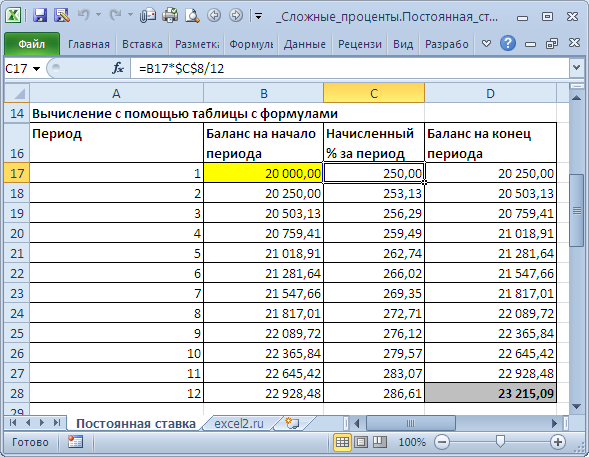
За 1-ый период будут начислены проценты в сумме =20000*(15%/12) , т.к. капитализация делается каждый месяц, а в году, как понятно, 12 мес. При начислении процентов за 2-ой период, в качестве базы, на которую начисляются %, нужно брать не исходную сумму вклада, а сумму вклада в конце первого периода (либо начале второго). И так дальше все 12 периодов.
Метод 2. Вычисление при помощи формулы Наращенных процентов Подставим в формулу наращенной суммы S = Р*(1+i )^n значения из задачки. S = 20000*(1+15%/12)^12 Нужно держать в голове, что в качестве процентной ставки необходимо указывать ставку за период (период капитализации). Иной вариант записи формулы – через функцию СТЕПЕНЬ() =20000*СТЕПЕНЬ(1+15%/12; 12)
Метод 3. Вычисление при помощи функции БС(). Функция БС() дозволяет найти будущую стоимость инвестиции при условии повторяющихся равных платежей и неизменной процентной ставки, т.е. она предназначена до этого всего для расчетов в случае аннуитетных платежей . Но, опустив 3-й параметр (ПЛТ=0), можно ее употреблять и для расчета сложных процентов. =-БС(15%/12;12;;20000)
Либо так =-БС(15%/12;12;0;20000;0)
Примечание . В случае переменной ставки для нахождения Будущей цены по способу сложных процентов употребляется функция БЗРАСПИС() .
Определяем сумму начисленных процентов
Разглядим задачку: Клиент банка положил на депозит 150 000 р. на 5 лет с каждогодним начислением сложных процентов по ставке 12 % годичных. Найти сумму начисленных процентов.
Сумма начисленных процентов I равна разности меж величиной наращенной суммы S и исходной суммой Р. Используя формулу для определения наращенной суммы S = Р*(1+i )^n, получим: I = S – P= Р*(1+i)^n – Р=P*((1+i)^n –1)=150000*((1+12%)^5-1) Итог: 114 351,25р. Для сопоставления: начисление по обычной ставке даст итог 90 000р. (см. файл примера ).
Определяем Срок долга
Разглядим задачку: Клиент банка положил на депозит некоторую сумму с каждогодним начислением сложных процентов по ставке 12 % годичных. Через какой срок сумма вклада удвоится? Логарифмируя обе части уравнения S = Р*(1+i)^n, решим его относительно неведомого параметра n.
В файле примера приведено решение, ответ 6,12 лет.
Вычисляем ставку сложных процентов
Разглядим задачку: Клиент банка положил на депозит 150 000 р. с каждогодним начислением сложных процентов. При какой годичный ставке сумма вклада удвоится через 5 лет?
В файле примера приведено решение, ответ 14,87%.
Примечание . О действенной ставке процентов читайте в данной нам статье .
Учет (дисконтирование) по сложным процентам
Дисконтирование основывается на базе концепции цены средств во времени: средства, доступные в истинное время, стоят больше, чем та же самая сумма в будущем, вследствие их потенциала обеспечить доход. Разглядим 2 вида учета: математический и банковский.
Математический учет . В этом случае решается задачка оборотная наращению по сложным процентам, т.е. вычисления выполняются по формуле Р=S/(1+i )^n Величину Р, полученную дисконтированием S, именуют современной, либо текущей стоимостью, либо приведенной величиной S. Суммы Р и S эквивалентны в том смысле, что платеж в сумме S через n лет равноценен сумме Р, выплачиваемой в реальный момент. Тут разность D = S — P именуется дисконтом.
Пример . Через 7 лет страхователю будет выплачена сумма 2000000 руб. Найти современную стоимость суммы при условии, что применяется ставка сложных процентов в 15% годичных. Иными словами, понятно: n = 7 лет, S = 2 000 000 руб., i = 15% .
Решение. P = 2000000/(1+15% )^7 Значение текущей цены будет меньше, т.к. открыв сейчас вклад на сумму Р с каждогодней капитализацией по ставке 15% мы получим через 7 лет сумму 2 млн. руб.
Этот же итог можно получить при помощи формулы =ПС(15%;7;;-2000000;1) Функция ПС() возвращает приведенную (к текущему моменту) стоимость инвестиции и рассмотрена тут .
Банковский учет . В этом случае предполагается внедрение сложной учетной ставки. Дисконтирование по сложной учетной ставке осуществляется по формуле: Р = S*(1- dсл )^n где dcл — непростая годичная учетная ставка.
При использовании сложной учетной ставки процесс дисконтирования происходит с прогрессирующим замедлением, потому что учетная ставка всякий раз применяется к сумме, уменьшенной за предшествующий период на величину дисконта.
Сравнив формулу наращения для сложных процентов S = Р*(1+i )^n и формулу дисконтирования по сложной учетной ставке Р = S*(1- dсл )^n придем к выводу, что заменив символ у ставки на обратный, мы можем для расчета дисконтированной величины употреблять все три метода вычисления наращения по сложным процентам, рассмотренные в разделе статьи Начисление процентов пару раз в год .
Непростой процент в Excel
Разберем разные формулы расчета процентов в Excel, для этого разглядим настоящие практические примеры, формулы и типовые денежные задачки.
Формула расчета процентов. Базисные понятия
Проценты (латин. pro centum) — являются неотъемлемой частью денежной арифметики и употребляются в банковском секторе, денег, бухгалтерии, страховании, налогообложении и т.д. Так в виде процентов выражают доходность и прибыльность компании, ставку по банковским кредитам и займам, налоговые ставки и т.д. Можно привести в доказательство значимости процентов в финансовом мире выражение А. Энштейна: «Сложные проценты — самая мощная сила в природе». Перед тем как разглядеть формулы расчета процентов введем главные определения и понятия.
- Капитал (англ.Capital,Principal) — является базой относительно которого вычисляют процент.
- Частота начисления процентов — период выплат процентов на капитал.
- Процентная ставка (англ.Rate) — размер процента либо толика капитала, который будет выплачен.
- Период вложения (англ.Period) — временной интервал передачи капитала банку либо другому денежному институту.
Итак, разглядим разные эконометрические задачки с процентами.
Формула расчета толики
Расчет толики нередко нужен в бухгалтерском и финансовом учете, где нужно найти долю тех либо других видов активов по отношению к суммарным. На рисунке ниже приведен пример и бухгалтерские данные по предприятию ОАО (форма организации публичной компании; акционерное общество) «АЛРОСА».
Пример задачки. Нужно высчитать долю «Припасов» в структуре «Активов» компании. Для этого воспользуемся формулой:
Толика припасов в Активах =B6/B7

Для того чтоб в ячейке приобретенные толики имею процентный вид можно пользоваться сочетанием кнопок «Ctrl» + «Shift» + «%».
Формула расчета размера процента от капитала
Разглядим вторую повсевременно встречающуюся экономическую задачку: расчет абсолютного значения процента по капиталу.
Пример задачки. Нужно найти размер выплаты банка ОАО (форма организации публичной компании; акционерное общество) «Альфа-банк» по вкладу в размере 100000 руб. с процентной ставкой 15%. Формула расчета размера выплат будет иметь последующий вид:
Выплаты по вкладу в банке =B6*B7

Формула расчета размера капитала с процентами
Пример задачки. Требуется высчитать итоговую стоимость продукта с НДС (налог на добавленную стоимость), тогда как стоимость продукта без НДС составляет 10000 руб., процентная ставка налога равна 18%. Формула расчета цены продукта с учетом НДС рассчитывается по формуле:
Стоимость продукта с учетом НДС =B6*(1+B7)

Формула уменьшения размера капитала на процент
Пример задачки. Нужно высчитать размер капитала опосля вычета налога на прибыль, процентная ставка налога равна 24%, текущее значение капитала равно 50000 руб. Формула расчета остатка капитала опосля вычета налога последующая:
Остаток капитала =B6-B6*B7

Формула расчета чистой цены капитала (продукции)
Пример задачки. Нужно высчитать исходную стоимость продукции без НДС (налог на добавленную стоимость), текущая стоимость продукции составляет 200000 руб., процентная ставка налога 18%. Формула расчета процентов последующая:
Стоимость продукции без НДС=B6/(1+B7)

Формула расчета обычных процентов по банковскому вкладу
При использовании обычных процентов выплаты по вкладу осуществляются лишь в конце срока (периода) размещения.
Пример задачки. Требуется высчитать размер выплат по банковскому вкладу, на который начисляется обыкновенные проценты. Размер вклада составляет 150000 руб., годичная процентная ставка по вкладу равна 12% (за 365 дней), период размещения вклада составляет 300 дней. Формула расчета в Excel последующая:
Размер банковского вклада на конец периода размещения =(1+B8*300/365)*B6

Формула расчета сложных процентов по банковскому вкладу
Сложные проценты различаются от обычных тем, что выплаты на банковский вклад осуществляются в течение периода его размещения.
Пример задачки. Нужно высчитать размер банковского вклада, который был расположен по непростой процент. Начальный размер депозита составляет 100000 руб., годичная процентная ставка равна 14%, период начисления процентов — любые 4 месяца, срок размещения вклада 1 год.
Формула расчета сложных процентов:
Размер вклада со сложными процентами на конец года =B6*(1+B8*B9/B7)^4

Способ сложных процентов имеет обширное внедрение в финансовом анализе и применяется для дисконтирования валютных потоков. Наиболее тщательно о способе дисконтирования читайте в статье: «Дисконтирование валютных потоков (DCF). Формула. Расчет в Excel».
Видео-урок: «Примеры расчета обычных и сложных процентов»
Резюме
Расчет процентов является неотъемлемой частью денежной арифметики и всей экономики в целом. Навык резвого расчета процентов в Excel дозволяет сберегать время при оценке будущей цены капитала.
БЗРАСПИС будущая стоимость инвестиций сложных процентов в Excel
Функция БЗРАСПИС в Excel вычисляет будущую стоимость инвестиции на основании узнаваемых данных о исходной цены (начальной сумме) и ряда значений сложных процентов, и возвращает соответственное числовое значение.
Расчет будущей цены инвестиций по плану ставок сложных процентов
При заключении неких денежных сделок употребляют так именуемые «сложные проценты» — когда процентная ставка изменяет свое значение с каждым следующим периодом выплат либо через остальные установленные периоды времени. К примеру, клиент сделал депозит в банк, заключив договор, по условию которого изначальная процентная ставка (к примеру, 12%) будет раз в год возрастать на 1%. В этом случае обыденные функции для расчета аннуитета не подступают.
Пример 1. По условиям кредитного контракта, клиент будет выплачивать определенные суммы за внедрение денежного продукта в протяжении 6 месяцев, при всем этом 1-ые 2 месяца будет действовать ставка 14%, а в следующие она будет повышена до 17%. Сумма, взятая в долг, — 15000 рублей. Найти фактическую сумму, которую выплатит клиент банка.
Вид таблицы данных:
Для определения общей суммы кредита (будущей цены инвестиции) используем функцию массива CTRL+SHIFT+Enter:
Так как в условии задачки указаны годичные ставки, а платежи производятся каждый месяц, нужно поделить каждую ставку на число месяцев в году (получить приведенное значение ставки). Так как вычисления производятся для всякого элемента массива B2:B7, обозначенные выше функция обязана быть введена в качестве формулы массива.
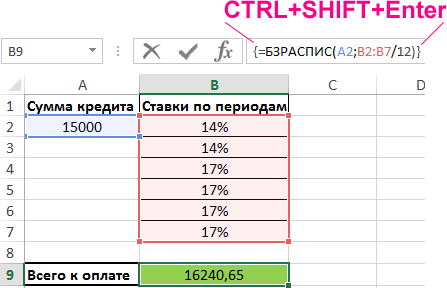
В итоге вычисления формулы получаем будущую стоимость инвестиций с переменной процентной ставкой.
Расчет годичный доходности инвестиций в процентах в Excel
Пример 2. В таблице указаны данные о доходах в процентах некого вкладывательного фонда (отрицательные значения свидетельствуют о понесенных убытках) в протяжении 1-го года. Найти процент возвращаемых средств фондом за год.
Вид таблицы данных:
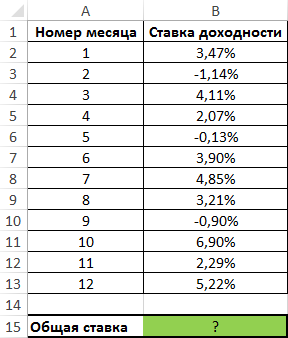
Примем исходную стоимость инвестиций за 1. Тогда для расчета используем последующую формулу:
В ячейке с формулой установим Процентный формат данных. Приобретенное значение:
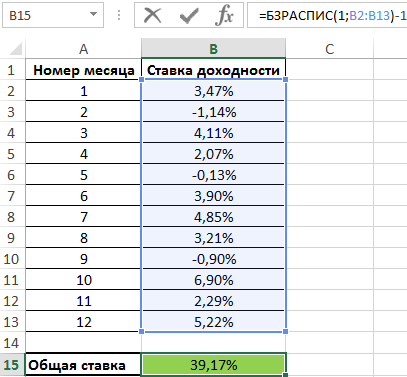
Cравнение силы роста обычных и сложных процентов в Excel
Пример 3. Клиенту банка предложили два разных варианта депозитного вклада: с фиксированными либо сложными процентами. Высчитать наиболее прибыльный для клиента вариант по показателю будущей цены, если:
- Сумма вклада составляет 100000 рублей.
- Период деяния контракта – 5 лет.
- Фиксированная ставка – 14,5%.
- Сложные проценты: каждогоднее повышение ставки на 0,5%, изначальное значение – 13,5%.
Вид таблицы данных:
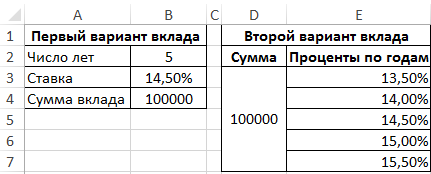
Для расчетов используем последующую формулу:
При помощи функции ЕСЛИ сравниваем значения, которые возвратили функция БС (для обычных процентов) и БЗРАСПИС (для сложных процентов) и выводим итог с пояснением.
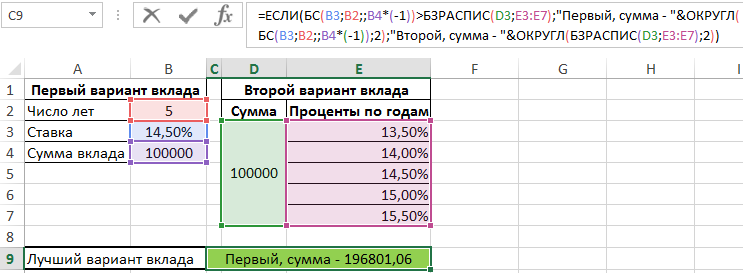
По сути, различие несущественное при пятилетнем сроке:
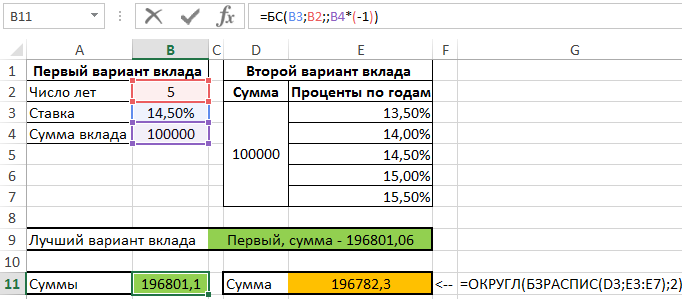
Но, если по истечению 5 лет контракт будет продлен с теми же критериями (повышение ставки на 0,5% раз в год), 2-ой вариант окажется наиболее прибыльным.
Расчет сложных процентов с пополнением

Допустим мы желаем приобрести жилище за 1 500 000 рублей. Покупку желаем создать через 10 лет.
Возникает вопросец, какую сумму нужно класть в банк любой год, чтоб через 10 лет получить 1 млн. 500 тыс? По идее стоит открыть вклад и накапливать. Ставка по депозиту в банке — 10% годичных.
Идет речь о вкладе с капитализацией, капитализация любой год, под 10 процентов в год. Вопросец, какую сумму необходимо откладывать с заработной платы? Необходимо осознавать, является ли эта сумма большенный и хватит ли оставшихся средств на жизнь? Зная ординарную формулу, описанную ниже, можно без усилий все посчитать.
Вы сможете употреблять калькулятор скоплений для ответа на этот вопросец.
Советуем: Калькулятор «Как накопить на квартиру?»
Формула расчета сложных процентов с пополнением
- FV — планируемая сумма,
- i — годичная процентная ставка(будьте внимательны, она идет в 10-х и сотых толиках),
- n — срок вероятного вклада в годах
- PMT — сумма пополнения вклада раз в период начисления.
- m — количество периодов в году(если раз в день, то 365)
В нашем случае имеем последующие данные
| Условия по вкладу | |
|---|---|
| Планируемая сумма FV | 1 млн. 500 тыс |
| Ставка i | 10% |
| Срок n | 10 лет, начисление раз в год |
| Капитализация процентов | Да |
Мы можем выразить из формулы подходящий нам каждогодний взнос 
Подставив в эту формулу наши значения получим 
94118,09232 — конкретно эту сумму мы должны вкладывать любой год, чтоб получить через 10 лет 1.5 млн. рублей.
Но по сути этот расчет ориентировочный. Четкий расчет можно получить при помощи калькулятора вкладов 
Выше приведен расчет депозита на 10 лет с 2 июля 2009. Каждогоднее пополнение 94118,09232
Сумма вышла приблизительно таковой(разница 35 рублей не существенна)
Полезные инструменты
А что если начальная сумма не нулевая
Если у вас стоит незначительно иная задачка — сколько необходимо пополнять текущий вклад, если сумма вклада равна 100 тыс. и требуется накопить 1.5 млн. рублей за 10 лет при ставке 10% годичных.
В таком случае, нашу начальную формулу необходимо незначительно видоизменять, добавив в нее часть, связанную с начальным взносом

В данной нам формуле А — начальная сумма вклада, а 2-ая часть слагаемого — это формула сложных процентов(процент с капитализацией)
Уже из данной нам форумлы необходимо выразить PMT — каждомесячный взнос. Но это уже дело арифметики для вас необходимо попытаться самому(ой). Если не получится, пишите в комментах, я ее приведу.
Данные формулы являются всепригодными и подступают для расчета вероятного срока депозита(когда вы понимаете, сколько будете пополнять и какую сумму желаете добиться)
В этом случае для вас будет увлекателен срок, необходимо просто выразить переменную n.
Ограничения и область применимости формул
Но стоит учесть, что данные расчеты подступают для студентов при решении задач, но не работают при четких банковских расчетах. Тут для вас может посодействовать депозитный калькулятор, так как он учитывает даты, выходные, ставку рефинансирования ЦБ. Т.е. данная формула не учитывает налог по депозиту. Налог же зависит от ставки рефинансирования ЦБ и валюты вклада.
Т.е. данный расчет будет приблизителен в любом случае. Здесь нет учета числа дней в году также. Но, если даны эталонные условия, как это делается в студенческих задачках, данную формулу можно с фуррором использовать в их решении.
Данная формула дозволяет получить ответ на последующие вопросцы:
- Сколько я накоплю, если буду откладывать 10 тыс. рублей каждый месяц?
- Сколько мне необходимо откладывать раз в год, чтоб накопить на квартиру в сумме 2 млн. рублей?
- Как длительно мне необходимо вкладывать 10 тыс. рублей, пополняя вклад, чтоб достигнуть суммы 500 тыс. рублей(стоимость простого авто)
- Как решить ту либо иную финансовую задачку, связанную с валютными потоками. Ведь может оказаться, что 1-ый год пополняли по 100 тыс, а 2-ой по 50 тыс. Как в этом случае посчитать предполагаемый доход и сумму в конце срока.
Формула быть может удачно применена для прогнозирования дохода по вашим средствам в банке — будь то вклад либо доходная карта

Полезное по теме
комменты
Здрасти, мне необходимо выяснить, какая будет сумма на депозите, если начальный взнос 20 000, каждомесячное пополнение 1 000, каждомесячное начисление 3%, срок 1 год, что то не то либо не так я вставляю в формулу! Подскажите пожалуйста как верно вставить эти данные!
Ставку необходимо указывать годичную
Все зависит от дат пополнения
В екселе попытайтесь…
Быстрее всего где нить ошиблись
Пробую подставить данные по формуле с пополнением и начальной не нулевой суммой. Пополнение каждомесячное схожего размера, на старте та же сумма. Итог не сходится даже близко. Что-то не верно подставил
Сколько нужно вкладывать каждый месяц заемщику в вкладывательный фонд под 10% годичных, чтоб через 10 лет накопить 10 млн рублей? С решением пожалуйста
Помогите решить пожалуйста!
Вклад 100 тыс. руб. был помещен на 0.5 года под 8 % годичных, инфляция за год составила 10%. Найти настоящий доход вкладчика исходя из убеждений покупательной возможности.
В ответ введите значение в тыс. руб. в виде целого числа.
с «m» уже разобралась, в моем случае это будет 12. а с PMT подскажите, пожалуйста!
Выведите, пожалуйста, из крайней формулы PMT, у меня какая-то ерунда выходит. И, я так понимаю, это будет каждогодная сумма пополнения вклада?
И еще вопросец: если капитализация каждомесячная в течении 10-летнего вклада, то «m» будет 12*10=120?
Спасибо за ответ!
Извиняюсь, разобрался: оказывается, срок «n» необходимо задавать в годах, тогда всё работает как следует. Мало неловко задавать 3, 6 и 9 месяцев (а это пользующиеся популярностью сроки вкладов), но ничего, приспособился. 🙂
Совершенно, непревзойденно и просто изложено, спасибо. Лишь тут нашёл нужные формулы.
Кажется, есть некорректность в формуле с ненулевой начальной суммой вклада:
по втором члене необходимо возводить в степень «n», а не «m*n».
Хороший денек. C что вы взяли?
Помогите решить пожалуйста!
Обладатель векселя номинальной стоимостью 10 млн. руб. учел его в банке за 6 мес. до срока погашения по учетной ставке 40% годичных. Обусловьте дисконт банка.
В ответ введите значение в млн. в виде целого числа.
Вклад 200 тыс. руб. был помещен на 0.5 года под 10 % годичных, инфляция за год составила 12%. Найти настоящий доход вкладчика исходя из убеждений покупательной возможности.
В ответ введите значение в тыс. руб. в виде целого числа.
Кредит, в сумме 500 тыс. руб., выдан на полгода, под 20% годичных. Найти общую сумму выплат по кредиту.
В ответ введите значение в тыс. руб. в виде целого числа.
Функцию глобальных средств более много делают:
СДР, золото, евро, бакс
золото, евро, бакс
СДР, золото
Кредит, в сумме 400 тыс. руб., выдан на 0.5 года, под 20% годичных. Найти общую сумму выплат по кредиту.
В ответ введите значение в тыс. руб. в виде целого числа.
Вид короткосрочного кредита, погашаемый по первому требованию, — это:
срочная ссуда
ипотечный кредит
онкольный кредит
Вклад 200 тыс. руб. был помещен на 1 год под 12 % годичных, инфляция за год составила 10%. Найти настоящий доход вкладчика исходя из убеждений покупательной возможности.
В ответ введите значение в тыс. руб. в виде целого числа.
Верный ответ введите в текстовое поле в виде числа.
Скорость воззвания средств = 2 М2 = 20 миллиардов. руб. Найти PQ.
Ответ отдать в виде целого числа.
Обладатель векселя номинальной стоимостью 1 млн. руб. учел его в банке за 6 мес. до срока погашения по учетной ставке 40% годичных. Обусловьте дисконт банка.
В ответ введите значение в млн., округлив до 1-го знака опосля точки. В качестве разделителя целой и дробной части используйте точку.
Размер Дм в стране на конец года составляла 300 миллиардов. руб. ЦБ выполнил доп эмиссию средств в размере 3 миллиардов. руб. и установил норму неотклонимых резервов в размере — 10%. Каковой будет размер валютной массы в стране?