Формула мат ожидания в excel

Среднее подборки либо выборочное среднее (sample average, mean) представляет собой среднее арифметическое всех значений подборки.

В MS EXCEL для вычисления среднего подборки можно употреблять функцию СРЗНАЧ() . В качестве аргументов функции необходимо указать ссылку на спектр, содержащий значения подборки.

Выборочное среднее является «неплохой» (несмещенной и действенной) точечной оценкой математического ожидания случайной величины (см. ниже), т.е. среднего значения начального распределения, из которого взята подборка.

Примечание: О вычислении доверительных интервалов при оценке математического ожидания можно прочесть, к примеру, в статье Доверительный интервал для оценки среднего (дисперсия известна) в MS EXCEL.

Некие характеристики среднего арифметического:

Сумма всех отклонений от среднего значения равна 0:

Если к любому из значений x_i прибавить одну и туже константу с, то среднее арифметическое возрастет на такую же константу;
Если каждое из значений x_i помножить на одну и туже константу с, то среднее арифметическое умножится на такую же константу.

Математическое ожидание

Среднее значение можно вычислить не только лишь для подборки, но для случайной величины, если понятно ее распределение. В этом случае среднее значение имеет особое заглавие – Математическое ожидание. Математическое ожидание охарактеризовывает «центральное» либо среднее значение случайной величины.

Примечание: В английской литературе имеется огромное количество определений для обозначения математического ожидания: expectation, mathematical expectation, EV (Expected Value), average, mean value, mean, E[X] либо first moment M[X].

Если случайная величина имеет дискретное распределение, то математическое ожидание рассчитывается по формуле:

где x_i – значение, которое может принимать случайная величина, а р(x_i) – возможность, что случайная величина воспримет это значение.

Если случайная величина имеет непрерывное распределение, то математическое ожидание рассчитывается по формуле:

где р(x) – плотность вероятности (конкретно плотность вероятности, а не возможность, как в дискретном случае).

Для всякого распределения, из представленных в MS EXCEL, Математическое ожидание можно вычислить аналитически, как функцию от характеристик распределения (см. надлежащие статьи про распределения). К примеру, для Биномиального распределения среднее значение равно произведению его характеристик: n*p (см. файл примера ).

Функция СРОТКЛ в Excel употребляется для анализа числового ряда, передаваемого в качестве аргумента, и возвращает число, соответственное среднему значению, рассчитанному для модулей отклонений относительно среднего арифметического для исследуемого ряда.

Примеры способов анализа числовых рядов в Excel

Смысл данной функции становится максимально ясен опосля рассмотрения примера. Допустим, в протяжении суток любые 3 часа фиксировались характеристики температуры воздуха. Был получен последующий ряд значений: 16, 14, 17, 21, 25, 26, 22, 18. При помощи функции СРЗНАЧ можно найти среднее значение температуры – 19,88 (округлим до 20). Для определения отличия всякого значения от среднего нужно отнять из него приобретенное среднее значение. К примеру, для первого замера температуры это будет равно 16-20=-4. Получаем ряд значений: -4, -6, -3, 1, 5, 6, 2, -2. Так как СРОТКЛ по определению работает с модулями отклонений, итоговый ряд значений имеет вид: 4, 6, 3, 1, 5, 6, 2, 2. Сейчас необходимо получить среднее значение для данного ряда при помощи функции СРЗНАЧ – приблизительно 3,63. Конкретно такой метод работы рассматриваемой функции.

Таковым образом, значение, вычисляемое функцией СРОТКЛ, можно высчитать при помощи формулы массива без использования данной функции. Допустим, перечисленные результаты замеров температур записаны в столбец (ячейки A1:A8). Тогда для определения среднего значения отклонений можно употреблять формулу =СРЗНАЧ(ABS(A1:A8-СРЗНАЧ(A1:A8))). Но, рассматриваемая функция существенно упрощает расчеты.

Пример 1. Имеются два ряда значений, представляющих из себя результаты наблюдений 1-го и такого же физического явления, изготовленные в ходе 2-ух разных тестов. Найти, среднее отклонение от среднего значения результатов для какого опыта является наибольшим?

Вид таблицы данных:

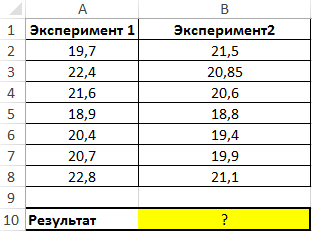
Используем последующую формулу:

Сравниваем результаты, возвращаемые функцией СРОТКЛ для первого и второго ряда чисел с внедрением функции ЕСЛИ, возвращаем соответственный итог.

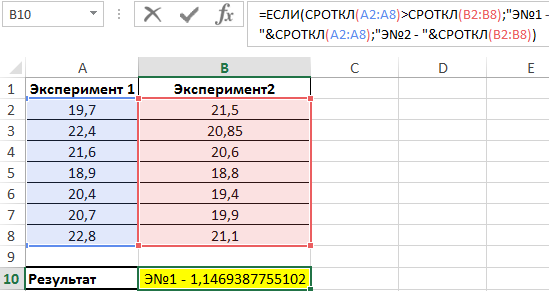
В итоге мы получили среднее отклонение от среднего значения. Это очень увлекательная функция для технического анализа денежных рынков, прогнозов курсов валют и даже дозволяет повысить шансы выигрышей в лотереях.

Формула расчета линейного коэффициента варианты в Excel

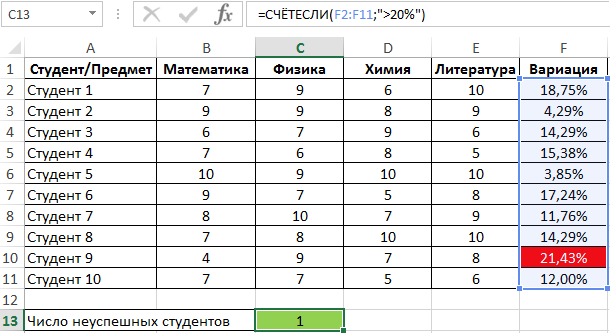
Пример 2. Студенты сдали экзамены по разным предметам. Найти число студентов, которые удовлетворяют последующему аспекту успеваемости – линейный коэффициент варианты оценок не превосходит 15%.

Вид таблицы данных:

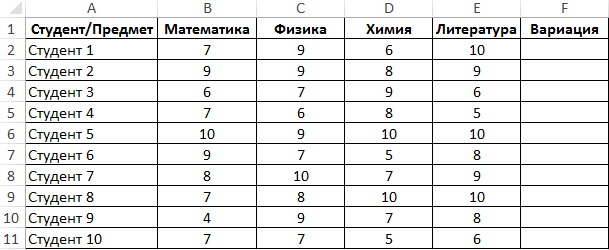
Линейный коэффициент варианты определяется как отношение среднего отличия к среднему значению. Для расчета используем последующую формулу:

Интересно почитать: Формула транспонирования в excel

Растянем ее вниз по столбцу и получим последующие значения:

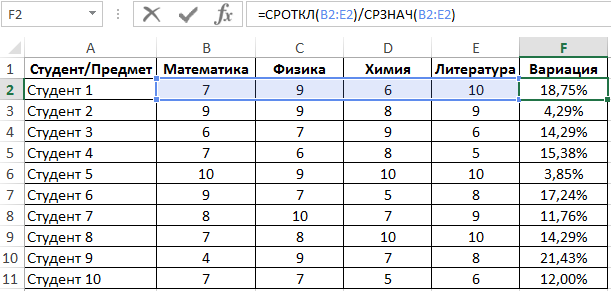
Для определения числа неуспешных студентов по обозначенному аспекту используем функцию:

Правила использования функции СРОТКЛ в Excel

Функция имеет последующий синтаксис:

=СРОТКЛ( число1 ;[число2];. )

число1 – неотклонимый, воспринимает числовое значение, характеризующее 1-ый член ряда значений, для которых нужно найти среднее отклонение от среднего;
[число2];… – необязательный, воспринимает 2-ое и следующие значения из исследуемого числового ряда.

При использовании функции СРОТКЛ удобнее задавать 1-ый аргумент в виде ссылки на спектр ячеек, к примеру =СРОТКЛ(A1:A8) заместо перечисления (=СРОТКЛ(A1;A2:A3…;A8)).
В качестве аргумента функции быть может передана константа массива, к примеру =СРОТКЛ(<2;5;4;7;10>).
Для получения достоверного результата нужно привести все значения ряда к единой системе измерения величин. К примеру, если часть длин указана в мм, а другие – в см, итог расчетов будет некорректен. Нужно конвертировать все значения в мм либо см соответственно.
Если в качестве аргументов функции переданы нечисловые данные, которые не могут быть преобразованы к числам, функция возвратит код ошибки #ЧИСЛО!. Если хотя бы одно значение из ряда является числовым, функция выполнит расчет, не возвращая код ошибки.
Не преобразуемые к числам текстовые строчки и пустые ячейки не учитываются в расчете. Если ячейка содержит значение 0 (нуль), оно будет учтено.
Логические данные автоматом преобразуются к числовым: ИСТИНА – 1, ЛОЖЬ – 0 соответственно.

Заглавие работы: Расчет математического ожидания, среднего квадратического отличия, дисперсии, при помощи программки Microsoft Excel

Категория: Лабораторная работа

Предметная область: Информатика, продажная девка империализма и программирование

Описание: Потому что функция математического ожидания это т оже самое что и функция среднего арифметического то: в пустой ячейке вводим = дальше жмем fx избираем функцию СРЗНАЧ выделяем числовые данные нашей начальной таблицы. Вычислить дисперсию: Вводим = дальше fx Статистические ДИСП выделить числовые данные.

Дата прибавления: 2014-02-08

Размер файла: 33.5 KB

Работу скачали: 269 чел.

Государственный Технический Институт Украины

„Киевский Политехнический Институт”

Факультет социологии и права

Лабораторная работа №2

Математические способы социологических исследовательских работ

„ Расчет математического ожидания, среднего квадратического отличия, дисперсии, при помощи программки Microsoft Excel”

студент 2 курса

1. Вычислить математическое ожидание:

1) Запуск > Все программки > Microsoft Office > Microsoft Excel

2) Потому что функция математического ожидания это т оже самое, что и функция среднего арифметического, то: в пустой ячейке вводим «=», дальше жмем fx, избираем функцию СРЗНАЧ, выделяем числовые данные нашей начальной таблицы.

2. Вычислить дисперсию:

Вводим =, дальше – fx, "Статистические" – "ДИСП", выделить числовые данные нашей начальной таблицы.

3. Среднее квадратичесое отклонение (не смещённое):

Вводим =, дальше – fx, "Статистические" – "СТАНДТОТКЛОН", выделить числовые данные нашей начальной таблицы.

4. Среднее квадратическое отклонение (смещённое):

Вводим =, дальше – fx, "Статистические" – "СТАНДТОТКЛОН", выделить числовые данные нашей начальной таблицы.

Вывод: Microsoft Excel является одной из самых комфортных компьютерных программ, при помощи которых можно рассчитать статические данные. В этом я удостоверился, когда высчитывал вышеуказанные данные.

Как отыскивать и вычислять для 2-ух среднее арифметическое значение

Под понятием среднего арифметического чисел предполагается итог легкой последовательности расчётов средней величины для ряда чисел, определённых заблаговременно. Нужно отметить, что такое значение в данное время обширно применяется спецами ряда отраслей. К примеру, известны формулы при проведении расчётов экономистами либо работниками статистической отрасли, где требуется иметь значение данного типа. Не считая этого, этот показатель интенсивно употребляют и в ряде остальных отраслей, которые являются смежными с вышеуказанными.

Одной из особенностей расчётов данного значения является простота процедуры. Провести расчёты сумеет хоть какой желающий. Для этого не нужно иметь особое образование. Нередко нет необходимости использовать и вычислительную технику.

В качестве ответа на вопросец как отыскать среднее арифметическое разглядим ряд ситуаций.

Подсчёт среднего арифметического пары

Самым обычным вариантом расчёта данной величины есть подсчёт её для 2-ух чисел. Процедура проведения расчёта в этом случае является весьма обычной:

Сначало требуется провести операцию сложения избранных чисел. Это нередко можно создать, как говорится, вручную, не используя электрическую технику.
Опосля того как сложение произведено и получен его итог нужно произвести деление. Данная операция предполагает разделение суммы 2-ух сложенных чисел на два – количество сложенных чисел. Конкретно такое действие и дозволит получить требуемую величину.

Интересно почитать: Среднее квадратичное отклонение в excel формула

Формула

Таковым образом, формула для подсчёта требуемой величины в случае с 2-мя будет смотреться последующим образом:

В данной формуле применяется последующее обозначение:

А и В – это заблаговременно избранные числа, для которых нужно отыскивать значение.

Нахождение значения для трёх

Проведение расчёта данной величины в ситуации, когда выбраны три числа, не будет очень различаться от предшествующего варианта:

Для этого следует избрать числа, нужные в расчёте, и сложить их для получения общей суммы.
Опосля того как данная сумма трёх будет найдена, требуется снова совершить функцию деления. При всем этом полученную сумму нужно поделить уже на три, что соответствует количеству избранных чисел.

Формула

Тем формула, нужная при проведении расчётов арифметического трёх, будет смотреться так:

В данной формуле принято последующее обозначение:

А, В и С – это числа, к которым нужно будет отыскивать среднее арифметическое.

Вычисление среднего арифметического четырёх

Как уже видно по аналогии с прошлыми вариациями вычисление данного значения для количества, равного четырём, будет носить последующий порядок:

Выбираются четыре числа, для которых нужно вычислить среднее арифметическое значение. Дальше делается суммирование и нахождение конечного результата данной процедуры.
Сейчас чтоб получить окончательный итог, следует взять полученную сумму четырёх и поделить её на четыре. Приобретенные данные и будут требуемым значением.

Формула

Из описанной чуть повыше последовательности действий по нахождению среднего арифметического для четырёх, можно получить последующую формулу:

В данной формуле переменные имеют последующее значение:

А, В, С и Е – это те, к которым нужно отыскать значение среднего арифметического.

Применяя данную формулу, постоянно можно будет вычислять требуемое значение для данного количества чисел.

Подсчёт среднего арифметического 5

Выполнение данной операции востребует проведения определённого метода действий.

До этого всего, нужно избрать 5 чисел, для которых будет проходить вычисление среднего арифметического. Опосля данного подбора эти числа, как и в прошлых вариантах, нужно просто сложить и получить конечную сумму.
Полученную сумму нужно будет поделить по их количеству на 5, что и дозволит получить требуемое значение.

Формула

Тем аналогично с ранее рассмотренными вариациями получаем такую формулу для подсчёта среднего арифметического:

В данной формуле переменные имеют такое обозначение:

А, В, С, Е и Р – это числа, для которых нужно получить среднее арифметическое.

Всепригодная формула вычисления

Проводя рассмотрение разных вариантов формул для вычисления среднего арифметического, можно направить внимание на то, что у их есть общая закономерность.

Потому практичнее будет использовать общую формулу для нахождения среднего арифметического. Ведь бывают ситуации, когда количество и величина расчётов быть может весьма большенный. Потому разумнее будет употреблять всепригодную формулу и не выводить всякий раз персональную технологию для расчёта данной величины.

Основным при определении формулы является принцип расчёта среднего арифметического.

Данный принцип как было видно из приведённых примеров, смотрится таковым образом:

Делается подсчёт количества чисел, которые заданы для получения требуемого значения. Эта операция быть может проведена как вручную при маленьком количестве чисел, так и с помощью вычислительной техники.
Проводится суммирование избранных чисел. Эта операция в большинстве ситуаций производится с помощью вычислительной техники, потому что числа могут состоять из 2-ух, трёх и наиболее цифр.
Сумма, которая получена в итоге сложения избранных чисел, обязана быть поделена на их количество. Данная величина определяется на начальном шаге расчёта среднего арифметического.

Таковым образом, общая формула для расчёта среднего арифметического ряда подобранных чисел будет смотреться последующим образом:

(А+В+…+N)/N

Данная формула содержит последующие переменные:

А и В – это числа, которые выбраны заблаговременно для расчёта их среднего арифметического.

N – это количество чисел, которые были взяты с целью проведения расчёта требуемого значения.

Подставляя всякий раз в данную формулу избранные числа, мы постоянно сможем получить требуемое значение среднего арифметического.

Как видно, нахождение среднего арифметического является легкой процедурой. Но нужно пристально относиться к проводимым вычислениям и проводить проверку приобретенного результата. Таковой подход разъясняется тем, что даже в самых обычных ситуациях существует возможность получения ошибки, которая может воздействовать позже на последующие расчёты. В связи с сиим рекомендуется использовать вычислительную технику, которая способна произвести подсчёты хоть какой трудности.

КАК: Как вычислить СРЕДНЕЕ в электрических таблицах Гугл — 2021

Существует несколько методов измеренияосновная тенденция либо, как его обычно именуют, среднее значение для набора значений.

Интересно почитать: Больше или равно в excel в формуле

Более нередко вычисляемая мера центральной тенденции — среднее арифметическое — либо обычное среднее — и рассчитывается методом суммирования группы чисел, а потом деления на подсчет этих чисел. К примеру, среднее значение, равное 4, 20 и 6, равно 10, как показано в строке 4.

В электрических таблицах Гугл есть ряд функций, которые упрощают поиск неких из более нередко применяемых средних значений. Они включают:

Функция AVERAGE — находит среднее арифметическое для перечня чисел.
Функция MEDIAN — находит среднее значение в перечне чисел.
Функция MODE — находит более нередко встречающееся значение в перечне чисел.

Синтаксис и аргументы СРЕДНЕЙ функции

Синтаксис функции относится к компоновке функции и включает в себя имя функции, скобки, разделители запятой и аргументы.

Синтаксис функции AVERAGE:

= СРЕДНЕЕ (число_1, номер_2, … номер_30)

number_1 — (требуется) данные, усредненные по функции
number_2 to number_30 — (необязательно) доп значения данных, которые должны быть включены в среднее значение. Наибольшее допустимое количество записей — 30

число аргументы могут содержать:

Перечень чисел, которые необходимо усреднить;
Сотовые ссылки на положение данных на листе;
Спектр ссылок на ячейки;
Именованный спектр.

Примечание. Текстовые записи и ячейки, содержащие логические значения (TRUE либо FALSE), игнорируются функцией, как показано в строчках 8 и 9 на изображении выше.

Если ячейки, которые являются пустыми либо содержат текстовые либо логические значения, потом изменены для хранения чисел, среднее значение пересчитывается для учета конфигураций.

Пустые ячейки против нуля

Когда дело доходит до поиска средних значений в электрических таблицах Гугл, существует разница меж пустым либо пустым ячеек и значениями, содержащими нулевое значение.

Бланк-ячейки игнорируются функцией AVERAGE, что быть может весьма комфортно, потому что это дозволяет просто отыскать среднее значение для несмежных ячеек данных, как показано в строке 6 выше.

Клеточки, содержащие нулевое значение, но, включены в среднее значение, как показано в строке 7.

Поиск функции AVERAGE

Как и во всех остальных интегрированных функциях в электрических таблицах Гугл, к функции AVERAGE можно получить доступ, щелкнувВставить > функция в меню, чтоб открыть раскрывающийся перечень нередко применяемых функций, который включает функцию AVERAGE.

В качестве кандидатуры, так как он так нередко употребляется, ярлычек функции был добавлен в панель инструментов программки, чтоб еще проще отыскивать и употреблять.

Значок на панели инструментов для данной и нескольких остальных фаворитных функций — это греческая буковка Sigma (Σ).

Гугл Spreadsheets СРЕДНИЙ пример функции

Ниже приведено описание того, как ввести функцию AVERAGE, показанную в четвертой строке, в примере на изображении выше, используя ярлычек к функции AVERAGE, упомянутой выше.

Ввод функции AVERAGE

Нажмите на ячейкуD4 — пространство, где будут отображаться результаты формулы.
Нажмитефункции значок на панели инструментов над листом, чтоб открыть раскрывающийся перечень функций.
Избрать Средний из перечня, чтоб расположить пустой копия функции в ячейке D4.
главный момент ячейки от A4 до C4 для ввода этих ссылок в качестве аргументов для функции и нажмитеВойти на клавиатуре.
Число 10 обязано показаться в ячейке D4. Это среднее из 3-х чисел — 4, 20 и 6.
Когда вы нажимаете на ячейку A8 полная функция = СРЕДНЯЯ (A4: C4) возникает в строке формул над листом.

Заметки

Отдельные ячейки, а не непрерывный спектр, могут быть добавлены в качестве аргументов, но любая ссылка на ячейку обязана быть разбита запятой.
Опосля ввода функции, если конфигурации внесены в данные в избранных ячейках, функция по дефлоту автоматом пересчитывает, чтоб отразить изменение.

Осознание ключа легенды и легенды в электрических таблицах Excel

Легенды делают графики Excel понятными, если вы узнаете, как их читать. Ах так легенда передает информацию. Обновлен для включения Excel 2019.

Поддерживаемые форматы электрических книжек и файлов для различных электрических книжек

Желаете выяснить, может ли ваш Kindle либо остальные электрические устройства показывать определенный файл? Вот удачный денди-график с поддерживаемыми форматами для разных электрических книжек.