Excel расчет кредитная карта excel

Кто как, а я считаю кредиты злом. В особенности потребительские. Кредиты для бизнеса — другое дело, а для обыденных людей мышеловка»средства за 15 минут, нужен лишь паспорт» срабатывает безотказно, предлагая наслаждение тут и на данный момент, а расплату за него когда-нибудь позже. И основная неувязка, по-моему, даже не в грабительских процентах либо в том, что это «позже» все равно когда-нибудь наступит. Кредит убивает мотивацию к росту. Для чего тужиться, обучаться, развиваться, находить доп источники дохода, если можно глупо зайти в ближний банк и там для тебя за полчаса оформят кредит на кабальных критериях, попутно хорошо разведя на страхование и остальные допы?

Так что весьма надеюсь, что изложенный ниже материал для вас не понадобится.

Но если уж случится так, что для вас либо вашим близким придется влезть в это дело, то хорошо бы перед походом в банк хотя бы приблизительно прикинуть суммы выплат по кредиту, переплату, сроки и т.д. «Помассажировать числа» заблаговременно, как я это называю Microsoft Excel может очень посодействовать в этом вопросце.

Вариант 1. Обычной кредитный калькулятор в Excel

Для резвой прикидки кредитный калькулятор в Excel можно создать за несколько минут при помощи всего одной функции и пары обычных формул. Для расчета каждомесячной выплаты по аннуитетному кредиту (т.е. кредиту, где выплаты выполняются равными суммами — таковых на данный момент большая часть) в Excel есть особая функция ПЛТ (PMT) из группы Денежные (Financial). Выделяем ячейку, где желаем получить итог, нажимаем на клавишу fx в строке формул, находим функцию ПЛТ в перечне и нажимаем ОК. В последующем окне необходимо будет ввести аргументы для расчета:

• Ставка — процентная ставка по кредиту в пересчете на период выплаты, т.е. на месяцы. Если годичная ставка 12%, то на один месяц обязано приходиться по 1% соответственно.
• Кпер — количество периодов, т.е. срок кредита в месяцах.
• Пс — исходный баланс, т.е. сумма кредита.
• Бс — конечный баланс, т.е. баланс с которым мы должны по идее придти к концу срока. Разумеется =0, т.е. никто никому ничего не должен.
• Тип — метод учета каждомесячных выплат. Если равен 1, то выплаты учитываются на начало месяца, если равен 0, то на конец. У нас в Рф абсолютное большая часть банков работает по второму варианту, потому вводим 0.

Также полезно будет прикинуть общий размер выплат и переплату, т.е. ту сумму, которую мы отдаем банку за временно внедрение его средств. Это можно создать при помощи обычных формул:

Вариант 2. Добавляем детализацию

Если охото наиболее детализированного расчета, то можно пользоваться еще 2-мя полезными финансовыми функциями Excel — ОСПЛТ (PPMT) и ПРПЛТ (IPMT). 1-ая из их вычисляет ту часть еще одного платежа, которая приходится на выплату самого кредита (тела кредита), а 2-ая может посчитать ту часть, которая придется на проценты банку. Добавим к нашему предшествующему примеру маленькую шапку таблицы с подробным расчетом и номера периодов (месяцев):

Функция ОСПЛТ (PPMT) в ячейке B17 вводится по аналогии с ПЛТ в прошлом примере:

Добавился лишь параметр Период с номером текущего месяца (выплаты) и закрепление знаком $ неких ссылок, т.к. потом мы эту формулу будем копировать вниз. Функция ПРПЛТ (IPMT) для вычисления процентной части вводится аналогично. Осталось скопировать введенные формулы вниз до крайнего периода кредита и добавить столбцы с ординарными формулами для вычисления общей суммы каждомесячных выплат (она постоянна и равна вычисленной выше в ячейке C7) и, ради энтузиазма, оставшейся сумме долга:

Чтоб создать наш калькулятор наиболее всепригодным и способным автоматом подстраиваться под хоть какой срок кредита, имеет смысл мало подправить формулы. В ячейке А18 лучше употреблять формулу вида:

Эта формула инспектирует при помощи функции ЕСЛИ (IF) достигнули мы крайнего периода либо нет, и выводит пустую текстовую строчку («») в том случае, если достигнули, или номер последующего периода. При копировании таковой формулы вниз на огромное количество строк мы получим номера периодов как раз до подходящего предела (срока кредита). В других ячейках данной для нас строчки можно употреблять похожую систему с проверкой на присутствие номера периода:

Т.е. если номер периода не пустой, то мы вычисляем сумму выплат при помощи наших формул с ПРПЛТ и ОСПЛТ. Если же номера нет, то выводим пустую текстовую строчку:

Вариант 3. Преждевременное погашение с уменьшением срока либо выплаты

Реализованный в прошлом варианте калькулятор хорош, но не учитывает один принципиальный момент: в настоящей жизни вы, быстрее всего, будете заносить доп платежи для преждевременного погашения при комфортной способности. Для реализации этого можно добавить в нашу модель столбец с доп выплатами, которые будут уменьшать остаток. Но, большая часть банков в схожих вариантах дают на выбор: сокращать или сумму каждомесячной выплаты, или срок. Любой таковой сценарий для наглядности лучше посчитать раздельно.

В случае уменьшения срока придется добавочно при помощи функции ЕСЛИ (IF) инспектировать — не достигнули мы нулевого баланса ранее срока:

А в случае уменьшения выплаты — поновой пересчитывать каждомесячный взнос начиная со последующего опосля преждевременной выплаты периода:

Вариант 4. Кредитный калькулятор с нерегулярными выплатами

Есть варианты кредитов, где клиент может платить нерегулярно, в любые произвольные даты внося любые имеющиеся суммы. Процентная ставка по таковым кредитам обычно выше, но свободы выходит больше. Можно даже взять в банке еще средств в дополнение к имеющемуся кредиту. Для расчета по таковой модели придется рассчитывать проценты и остаток с точностью не до месяца, а до денька:

Самостоятельный расчет Действенной Процентной Ставки

Чтож, давайте попробуем высчитать эффективную процентную ставку своими силами. Для того чтоб осилить это дело будет нужно не только лишь вооружиться калькулятором и программкой Excel, да и мало сморщить мозг (центральный отдел нервной системы животных, обычно расположенный в головном отделе тела и представляющий собой компактное скопление нервных клеток и их отростков), ибо для рассчета сумм и порядка кредитных платежей нам будет нужно освоить некие денежные формулы, которые «для обычных смертных» могут показаться не таковыми уж и явными.

Как без помощи других посчитать эффективную процентную ставку?

Давайте возьмем определенный пример и рассчитаем его.

• Сумма кредита: $100 000
• Годичная ставка: 18%
• Комиссия за сервис кредита: 1% от суммы (взимается каждый месяц)
• Срок кредитования: 12 месяцев
• Способ погашения: аннуитетные платежи.

Аннуитетный платеж значит, что, погашать кредит необходимо равными толиками в течение всего срока кредитования. Либо, просто говоря, каждый месяц нужно выплачивать схожую сумму. На мой взор это более удачный метод погашения кредита.

Для начала — узнаем размер каждомесячного платежа. Для этого нам будет нужно формула, приведенная в статье «Аннуитетные платежи».
Напомним, формула смотрится так:

A = K*S, где S — сумма кредита (в нашем случае S = 100 000); K — коэффициент аннуитета, рассчитывается по формуле, зависит от величин i и n.

В этом случае i = 0,015 n = 12. Если мы подставим приобретенные значения в вышеприведенную формулу, то получим, что

К = 0,09168.
А = $9168.

Но, можно создать мало проще. Для того, чтоб высчитать размер каждомесячного платежа, воспользуемся интегрированной в Excel функцией ПЛТ.

Вводим в ячейку формулу вида:

И получаем ту же сумму: $9168.

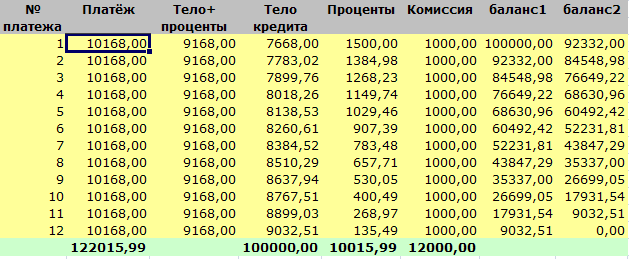
Сейчас нам необходимо составить в Excel’е таблицу каждомесячных платежей:

Cкачать таблицу расчёта в формате Excel

Если вы не до конца сообразили, как происходит рассчет — перечитайте статью и смотрите на формулы в строке состояния Excel

Так же направьте внимание, что с каждым месяцем выплаты процентов по кредиту уменьшаются, а выплаты главный части кредита растут. Это одна из особенностей аннуитетного метода погашения кредита.

Итоги расчета действенной процентной ставки

• Мы взяли кредит на $100 000.
• Выплатили $122015,99.
• Переплата составила $22015,99.
• Ставка 22015,99 / 100000 = 22%.

Каждомесячная комиссия в 1% обошлась нам в 12000 баксов, что превосходит основную сумму выплат по кредиту! Почему так? Поэтому что комиссию за сервис мы любой месяц платили из рассчета от главный суммы кредита ($100’000), а проценты с каждым месяцем уменьшались ввиду того, что каждый месяц уменьшалась сумма кредита. Видите ли, таковая, безопасная, на 1-ый взор, хитрость банка, как процент за сервис при ближнем рассмотрении обходится весьма недешево.

Хомячковый рай. Уйти и потеряться:

Формула действенной процентной ставки

Секрет действенной процентной ставки скрыт в указаниях Центробанка РФ (Российская Федерация — государство в Восточной Европе и Северной Азии, наша Родина) № 2008-У «О порядке расчета и доведения до заемщика (физического лица) полной цены кредита», датированных 13 мая 2008 года. Лучшая процентная ставка в виде формулы представлена таковым образом:

Обозначения знаков:

• di — дата первого денежного потока;
• d0 — дата выдачи суммы кредита;
• n — количество денежных потоков;
• ДПi — сумма первого денежного потока, прописанная в договоре;
• ПСК — полная стоимость кредита с учетом годичных процентов.

Не наименее пользующимся популярностью инвентарем для расчета прибыльной процентной ставки по версии Центробанка остается программка Excel, в частности ее формула ЧИСТВНДОХ.

Как вы имели возможность убедиться без помощи других, даже блестящие познания школьного курса арифметики навряд ли посодействуют «непосвященным» заемщикам разобраться в сложностях подсчета действенной процентной ставки. Необходимо отметить, что даже если вы осмелитесь наперевес с калькулятором атаковать денежные верхушки банковских подсчетов, то все равно навряд ли добьетесь обычных результатов. Все причина в том, что сложная система «укрытых» комиссий вровень со специфичностью оборота средств в денежных учреждениях очень сложна и непрозрачна, чтоб обычный юзер мог разобраться в ней без помощи других.

Так что «розовая» мечта без помощи других просчитать кредитные ставки и обезопасить себя от лишних выплат для почти всех плательщиков навечно остается такой. Эффективную банковскую ставку, рассчитанную по методике ЦБ, уместно употреблять разве что для сопоставления подобных предложений от различных банков для выбора рационального вида платежей.

Хомячковый рай. Уйти и потеряться:

Действенная процентная ставка (ЭПС). Расчёт ставки по кредиту

Обычно банки в борьбе за клиентов дают неописуемо прибыльные условия, в особенности в отношении кредитов. Почти все маркетинговые материалы строятся на том, что процентные ставки по кредитам конкретно в этом банке более низкие. Определенную величину данной для нас ставки, вправду весьма симпатичную, нередко изображают в качестве 1-го из главных частей маркетинговой композиции буклета либо постера. Но практически никто не удосуживается прочесть сносочку где-нибудь понизу либо сбоку, которая объясняет, что процентная ставка, — это еще не все и в дополнение к ней есть различные комиссионные платежи, количество и наименования которых зависят только от фантазии банкира. Потому будущему клиенту банка весьма полезно разобраться, какова же настоящая стоимость кредита, другими словами высчитать эффективную процентную ставку (сокращенно — ЭПС).

Разумеется, что из-за нежелания утратить даже малую часть прибыли банки идут на разные уловки и ухищрения. Потому объявленная и настоящая кредитные процентные ставки могут различаться никак не на толики процентов и естественно не в пользу клиента.

Величина действенной процентной ставки дозволяет сопоставить настоящие кредитные условия разных банковских учреждений и провести их беспристрастную оценку.

Как высчитать эффективную процентную ставку кредитной карты

Если взять в качестве обычного примера известную всем кредитную карту, то, рассчитывая ЭПС по ней, следует учесть комиссии банка — за ведение счета, за сервис самой карты и пр. Если банком предлагается льготный кредитный период, то рассчитывать ЭПС нужно для обоих вариантов — с льготой и без нее. Так как поведение заемщика предвидеть весьма трудно, при расчете ЭПС кредитной карты принимаются такие исходные условия: предел кредитования и размер задолженности равны, платежи вносятся равными толиками, срок кредита — 24 месяца.

В итоге выходит, что точную величину ЭПС кредитной карты рассчитать можно лишь примерно, в основном из-за непредсказуемости действий заемщика. Но в любом случае эта цифра будет намного больше заявленной банком.

Расчет ЭПС

В общем виде расчет действенной процентной ставки ведется согласно методики, утвержденной в Положении 254-П Центробанка Рф. При всем этом непременно следует учесть все сборы, проценты и комиссии, уплачиваемые заемщиком банку.