Расчет средневзвешенного значения в Excel

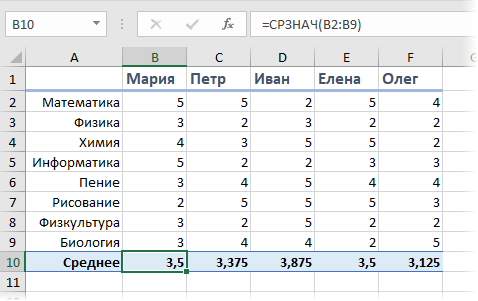
Представим, что мы с вами сидим в приемно-экзаменационной комиссии и оцениваем абитуриентов, которые желают поступить в наш ВУЗ. Оценки по разным предметам у наших кандидатов последующие:

Свободное пространство, допустим, лишь одно, и наша задачка — избрать достойного.

1-ое, что обычно приходит в голову — это высчитать традиционный средний балл при помощи обычной функции Excel СРЗНАЧ (AVERAGE).

На 1-ый взор кажется, что лучше всех подступает Иван, т.к. у него средний бал наибольший. Но здесь мы впору вспоминаем, что факультет-то наш именуется «Программирование», а у Ивана отличные оценки лишь по рисованию, пению и иной физической культуре, а по арифметике и информатике как раз не весьма. Возникает вопросец: как присвоить нашим предметам различную значимость (ценность), чтоб учесть ее при расчете среднего? И вот здесь на помощь приходит средневзвешенное значение.

Средневзвешенное — это среднее с учетом различной ценности (веса, значимости) всякого из частей.

В бизнесе средневзвешенное нередко употребляется в таковых задачках, как:

• оценка ранца акций, когда у каждой из их своя ценность/рисковость
• оценка прогресса по проекту, когда у задач не равный вес и значимость
• оценка персонала по набору способностей (компетенций) с разной значимостью для требуемой должности
• и т.д.

Расчет средневзвешенного формулами

Добавим к нашей таблице очередной столбец, где укажем некоторые безразмерные баллы значимости всякого предмета по шкале, к примеру, от 0 до 9 при поступлении на наш факультет программирования. Потом расчитаем средневзвешенный бал для всякого абитурента, т.е. среднее с учетом веса всякого предмета. Подходящая нам формула будет смотреться так:

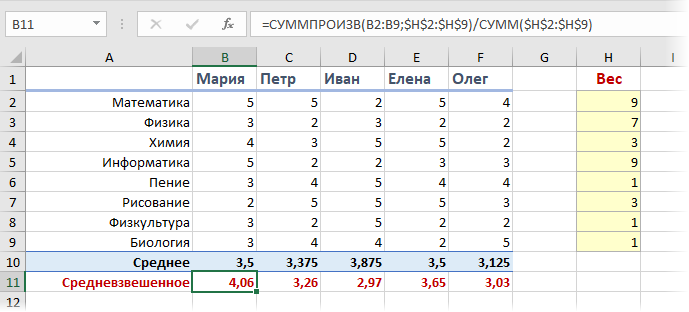
Функция СУММПРОИЗВ (SUMPRODUCT) попарно перемножает друг на друга ячейки в 2-ух обозначенных спектрах — оценки абитурента и вес всякого предмета — а потом суммирует все приобретенные произведения. Позже приобретенная сумма делится на сумму всех баллов значимости, чтоб усреднить итог. Вот и вся премудрость.

Так что берем Машу, а Иван пусть поступает в институт физкультуры 😉

Расчет средневзвешенного в сводной таблице

Поднимем ставки и усложним задачку. Допустим, что сейчас нам необходимо подсчитать средневзвешенное, но не в обыкновенной, а в сводной таблице. Представим, что у нас есть вот таковая таблица с данными по продажам:

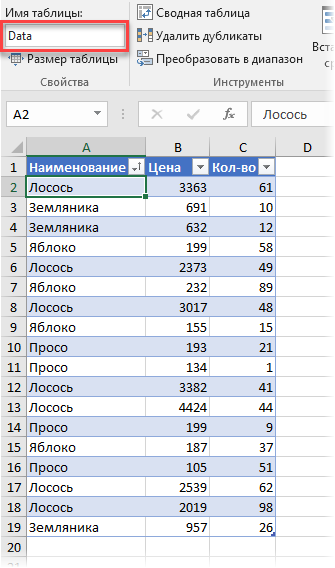
Направьте внимание, что я преобразовал ее в «умную» таблицу при помощи команды Основная — Форматировать как таблицу (Home — Format as Table) и отдал ей на вкладке Конструктор (Design) имя Data.

Заметьте, что стоимость на один и этот же продукт может различаться. Наша задачка: высчитать средневзвешенные цены для всякого продукта. Следуя той же логике, что и в прошлом пт, к примеру, для земляники, которая продавалась 3 раза, это обязано быть:

=(691*10 + 632*12 + 957*26)/(10+12+26) = 820,33

Другими словами мы суммируем цены всех сделок (стоимость каждой сделки множится на количество по сделке) и позже делим получившееся число на полное количество этого продукта.

Правда, с реализацией данной для нас нехитрой логики конкретно в сводной таблице нас ожидает маленький облом. Если вы работали со сводными ранее, то, наверняка, помните, что можно просто переключить поле значений сводной в подходящую нам функцию, щелкнув по нему правой клавишей мыши и выбрав команду Итоги по (Summarize Values By) :

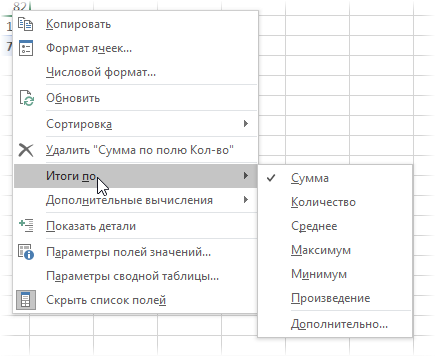
В этом перечне есть среднее, но нет средневзвешенного 🙁

Можно отчасти решить делему, если добавить в начальную таблицу вспомогательный столбец, где будет считаться стоимость каждой сделки:

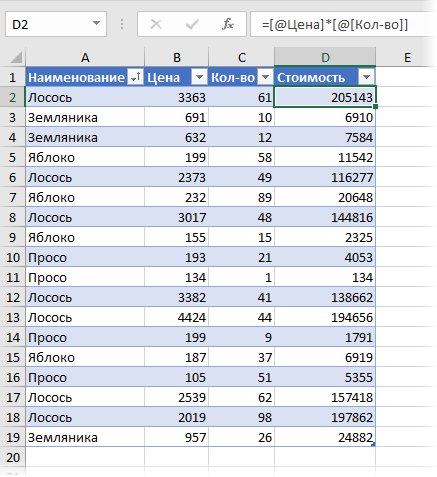
Сейчас можно рядом закинуть в область значений стоимость и количество — и мы получим практически то, что требуется:

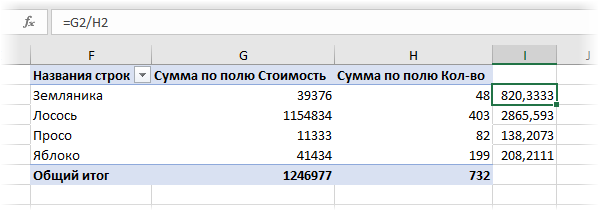
Остается поделить одно на другое, но создать это, как бы, обычное математическое действие снутри сводной не так просто. Придется или добавлять в сводную вычисляемое поле (вкладка Анализ — Поля, элементы, наборы — Вычисляемое поле), или считать обыкновенной формулой в примыкающих ячейках либо завлекать функцию ПОЛУЧИТЬ.ДАННЫЕ.СВОДНОЙ.ТАБЛИЦЫ (GET.PIVOT.DATA) , о которой я уже писал. А если завтра поменяются размеры сводной (ассортимент продуктов), то все эти формулы придется вручную корректировать.

В общем, как-то все неловко, трудоемко и нагоняет тоску. Да к тому же доп столбец в начальных данных необходимо руками созодать. Но прекрасное решение есть.

Расчет средневзвешенного в сводной таблице при помощи Power Pivot и языка DAX

Если у вас Excel 2013-2016, то в него встроен супермощный инструмент для анализа данных — надстройка Power Pivot, по сопоставлению с которой сводные таблицы с их способностями — как счеты против калькулятора. Если у вас Excel 2010, то эту надстройку можно совсем безвозмездно скачать с веб-сайта Microsoft и тоже для себя установить. При помощи Power Pivot расчет средневзвешенного (и остальных неосуществимых в обыденных сводных штук) весьма очень упрощается.

1. Для начала, загрузим нашу таблицу в Power Pivot. Это можно создать на вкладке Power Pivot клавишей Добавить в модель данных (Add to Data Model) . Раскроется окно Power Pivot и в нем покажется наша таблица.

2. Потом щелкните мышью в строчку формул и введите туда формулу для расчета средневзвешенного:

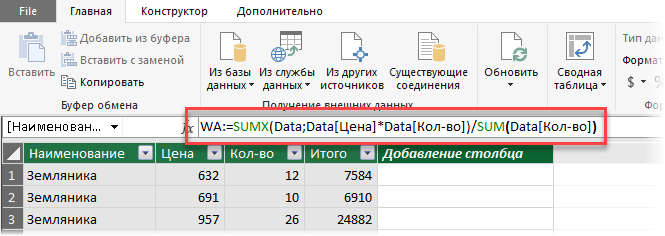
Несколько аспектов по формуле:

• В Power Pivot есть собственный интегрированный язык с набором функций, инструментов и определенным синтаксисом, который именуется DAX. Так что можно сказать, что эта формула — на языке DAX.
• Тут WA — это заглавие вычисляемого поля (в Power Pivot они еще именуются меры), которое вы придумываете сами (я называл WA, имея ввиду Weighted Average — «средневзвешенное» по-английски).
• Направьте внимание, что опосля WA идет не равно, как в обыкновенном Excel, а двоеточие и равно.
• При вводе формулы будут выпадать подсказки — используйте их.
• Опосля окончания ввода формулы необходимо надавить Enter , как и в обыкновенном Excel.

3. Сейчас строим сводную. Для этого в окне Power Pivot изберите на вкладке Основная — Сводная таблица (Home — Pivot Table). Вы автоматом вернетесь в окно Excel и увидите обычный интерфейс построения сводной таблицы и перечень полей на панели справа. Осталось закинуть поле Наименование в область строк, а нашу сделанную формулой меру WA в область значений — и задачка решена:

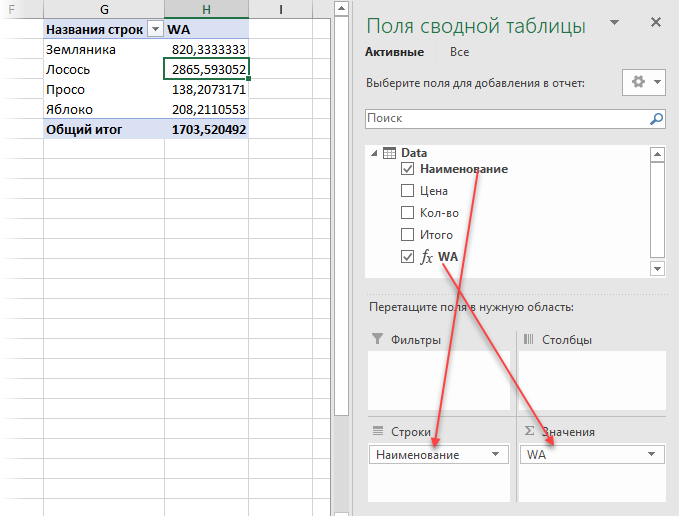
Вот так — прекрасно и роскошно.

Общая мораль: если вы много и нередко работаете со сводными таблицами и для вас их способности «тесны» — копайте в сторону Power Pivot и DAX — и будет для вас счастье!

Как отыскать среднее арифметическое число в Excel

Для того чтоб отыскать среднее значение в Excel (при том непринципиально числовое, текстовое, процентное либо другое значение) существует много функций. И любая из их владеет своими чертами и преимуществами. Ведь в данной задачке могут быть поставлены определенные условия.

К примеру, средние значения ряда чисел в Excel считают при помощи статистических функций. Можно также вручную ввести свою формулу. Разглядим разные варианты.

Как отыскать среднее арифметическое чисел?

Чтоб отыскать среднее арифметическое, нужно сложить все числа в наборе и поделить сумму на количество. К примеру, оценки школьника по информатике: 3, 4, 3, 5, 5. Что выходит за четверть: 4. Мы отыскали среднее арифметическое по формуле: =(3+4+3+5+5)/5.

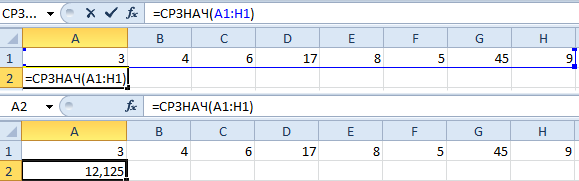
Как это стремительно создать при помощи функций Excel? Возьмем для примера ряд случайных чисел в строке:

1. Ставим курсор в ячейку А2 (под набором чисел). В основном меню – инструмент «Редактирование» — клавиша «Сумма». Избираем опцию «Среднее». Опосля нажатия в активной ячейке возникает формула. Выделяем спектр: A1:H1 и жмем ВВОД.
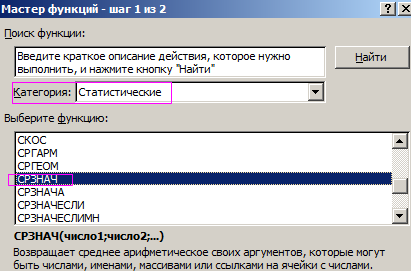
2. В базе второго способа этот же принцип нахождения среднего арифметического. Но функцию СРЗНАЧ мы вызовем по-другому. При помощи мастера функций (клавиша fx либо композиция кнопок SHIFT+F3).
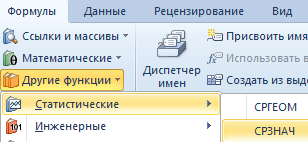
3. 3-ий метод вызова функции СРЗНАЧ из панели: «Формула»-«Формула»-«Остальные функции»-«Статические»-«СРЗНАЧ».

Либо: создадим активной ячейку и просто вручную впишем формулу: =СРЗНАЧ(A1:A8).

Сейчас поглядим, что еще умеет функция СРЗНАЧ.

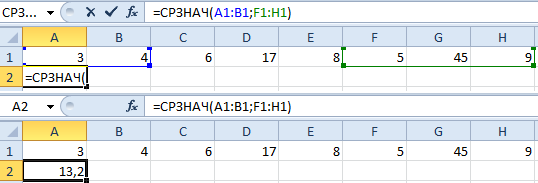
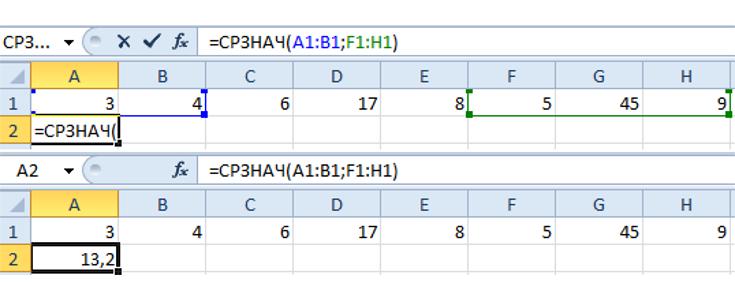
Найдем среднее арифметическое 2-ух первых и 3-х крайних чисел. Формула: =СРЗНАЧ(A1:B1;F1:H1). Итог:

Среднее значение по условию

Условием для нахождения среднего арифметического быть может числовой аспект либо текстовый. Будем применять функцию: =СРЗНАЧЕСЛИ().

Отыскать среднее арифметическое чисел, которые больше либо равны 10.

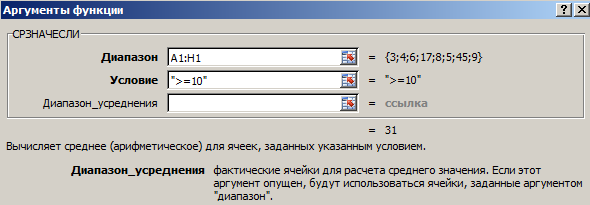Итог использования функции СРЗНАЧЕСЛИ по условию «>=10»:

3-ий аргумент – «Спектр усреднения» — опущен. Во-1-х, он не обязателен. Во-2-х, анализируемый программкой спектр содержит ТОЛЬКО числовые значения. В ячейках, обозначенных в первом аргументе, и будет выполняться поиск по прописанному во 2-м аргументе условию.

Внимание! Аспект поиска можно указать в ячейке. А в формуле создать на нее ссылку.

Найдем среднее значение чисел по текстовому аспекту. К примеру, средние реализации продукта «столы».

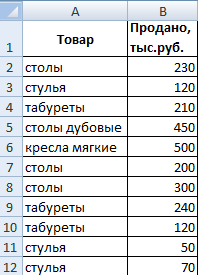
Функция будет смотреться так: =СРЗНАЧЕСЛИ($A$2:$A$12;A7;$B$2:$B$12). Спектр – столбец с наименованиями продуктов. Аспект поиска – ссылка на ячейку со словом «столы» (можно заместо ссылки A7 вставить само слово «столы»). Спектр усреднения – те ячейки, из которых будут браться данные для расчета среднего значения.

В итоге вычисления функции получаем последующее значение:

Внимание! Для текстового аспекта (условия) спектр усреднения указывать непременно.

Как посчитать средневзвешенную стоимость в Excel?

Как посчитать средний процент в Excel? Для данной для нас цели подходят функции СУММПРОИЗВ и СУММ. Таблица для примера:

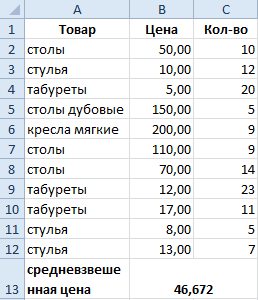
Как мы узнали средневзвешенную стоимость?

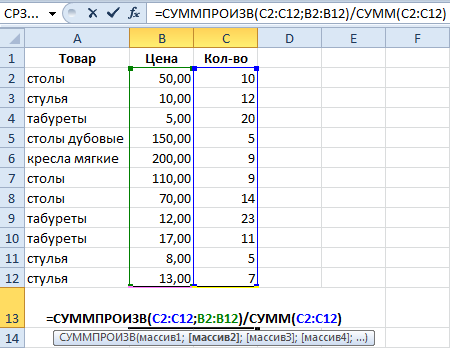
При помощи формулы СУММПРОИЗВ мы узнаем общую выручку опосля реализации всего количества продукта. А функция СУММ — сумирует количесвто продукта. Поделив общую выручку от реализации продукта на полное количество единиц продукта, мы отыскали средневзвешенную стоимость. Этот показатель учитывает «вес» каждой цены. Ее долю в общей массе значений.

Среднее квадратическое отклонение: формула в Excel

Различают среднеквадратическое отклонение по генеральной совокупы и по выборке. В первом случае это корень из генеральной дисперсии. Во 2-м – из выборочной дисперсии.

Для расчета этого статистического показателя составляется формула дисперсии. Из нее извлекается корень. Но в Excel существует готовая функция для нахождения среднеквадратического отличия.

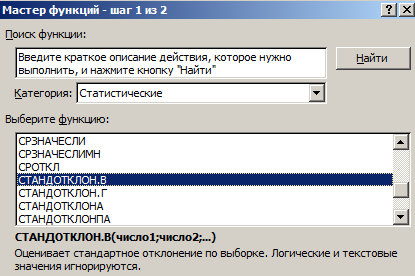
Среднеквадратическое отклонение имеет привязку к масштабу начальных данных. Для образного представления о варианты анализируемого спектра этого недостаточно. Чтоб получить относительный уровень разброса данных, рассчитывается коэффициент варианты:

среднеквадратическое отклонение / среднее арифметическое значение

Формула в Excel смотрится последующим образом:

СТАНДОТКЛОНП (спектр значений) / СРЗНАЧ (спектр значений).

Коэффициент варианты считается в процентах. Потому в ячейке устанавливаем процентный формат.

Как верно вычислить среднее значение?

Средняя заработная плата… Средняя длительность жизни… Фактически любой денек мы с вами слышим эти словосочетания, применяемые для описания огромного количества одним единственным числом. Но как ни удивительно, «среднее значение» — довольно каверзное понятие, нередко вводящее в заблуждение обыденного, неискушенного в математической статистике, человека.

В чем неувязка?

Под средним значением почаще всего предполагается среднее арифметическое, которое весьма очень варьируется под действием единичных фактов либо событий. И вы не получите настоящего представления о том, как конкретно распределены значения, которые вы исследуете.

Давайте обратимся к традиционному примеру со средней заработной платой.

В которой-то абстрактной компании работает 10 служащих. Девять из их получают заработную плату около 50 000 рублей, а один 1 500 000 рублей (по необычному совпадению он же является генеральным директором данной для нас компании).

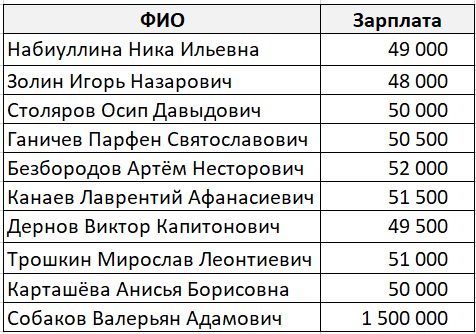
Средним значением в данном случае будет 195 150 рублей, что согласитесь, некорректно.

Какие методы вычисления среднего бывают?

Первым методом является вычисление уже упомянутого среднего арифметического, являющегося суммой всех значений, деленной на их количество.

• x – среднее арифметическое;
• x_n – конкретное значение;
• n – количество значений .

• Отлично работает при обычном распределении значений в выборке;
• Просто вычислить;
• Интуитивно понятно.

• Не дает настоящего представления о распределении значений;
• Неуравновешенная величина просто поддающаяся выбросам (как в случае с генеральным директором).

Вторым методом является вычисление моды, другими словами более нередко встречающегося значения.

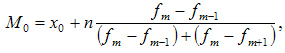
• M₀ – мода;
• x₀ – нижняя граница интервала, который содержит моду;
• n – величина интервала;
• f_m– частота (сколько раз в ряду встречается то либо другое значение);
• f_m-1 – частота интервала предыдущего модальному;
• f_m+1 – частота интервала последующего за модальным.

• Отлично подступает для получения представления о публичном мировоззрении;
• Отлично подступает для нечисловых данных (цвета сезона, хиты продаж, рейтинги);
• Ординарна для осознания.

• Моды может просто не быть (нет повторов);
• Мод быть может несколько (многомодальное распределение).

3-ий метод — это вычисление медианы, другими словами значения, которое разделяет упорядоченную подборку на две половины и находится меж ними. А если такового значения нет, то за медиану принимается среднее арифметическое меж границами половин подборки.

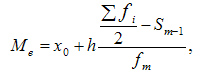
• M_e – медиана;
• x₀ – нижняя граница интервала, который содержит медиану;
• h – величина интервала;
• f _i – частота (сколько раз в ряду встречается то либо другое значение);
• S_m-1 – сумма частот интервалов предыдущих медианному;
• f_m – число значений в медианном интервале (его частота).

• Дает самую близкую к реальности и репрезентативную оценку;
• Устойчива к выбросам.

• Труднее вычислить, потому что перед вычислением подборку необходимо упорядочить.

Мы разглядели главные способы нахождения среднего значения, называющиеся мерами центральной тенденции (по сути их больше, но это более пользующиеся популярностью).

А сейчас давайте вернемся к нашему примеру и посчитаем все три варианта среднего с помощью особых функций Excel:

• СРЗНАЧ(число1;[число2];…) — функция для определения среднего арифметического;
• МОДА.ОДН(число1;[число2];. ) — функция моды (в наиболее старенькых версиях Excel использовалась МОДА(число1;[число2];. ) );
• МЕДИАНА(число1;[число2];. ) — функция для поиска медианы.

И вот какие значения у нас вышли:

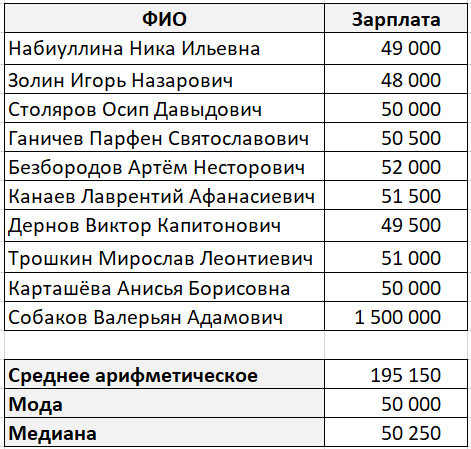
В этом случае мода и медиана еще лучше охарактеризовывают среднюю заработную плату в компании.

Но что созодать, когда в выборке не 10 значений, как в примере, а миллионы? В Excel это не посчитать, а вот в базе данных где хранятся ваши данные, без заморочек.

Вычисляем среднее арифметическое на SQL

Здесь все довольно просто, потому что в SQL предусмотрена особая агрегатная функция AVG .

И чтоб ее применять довольно написать вот таковой запрос:

Вычисляем моду на SQL

В SQL нет отдельной функции для нахождения моды, но ее просто и стремительно можно написать без помощи других. Для этого нам нужно выяснить, какая из зарплат почаще всего повторяется и избрать более пользующуюся популярностью.

Вычисляем медиану на SQL

Как и в случае с модой, в SQL нет интегрированной функции для вычисления медианы, зато есть всепригодная функция для вычисления процентилей PERCENTILE_CONT .

Смотрится все это так:

Подробнее о работе функции PERCENTILE_CONT лучше почитать в справке Microsoft и Гугл BigQuery.

Какой метод все-же применять?

Из произнесенного выше следует, что медиана наилучший метод для вычисления среднего значения.

Но это не постоянно так. Если вы работаете со средним, то остерегайтесь многомодального распределения:

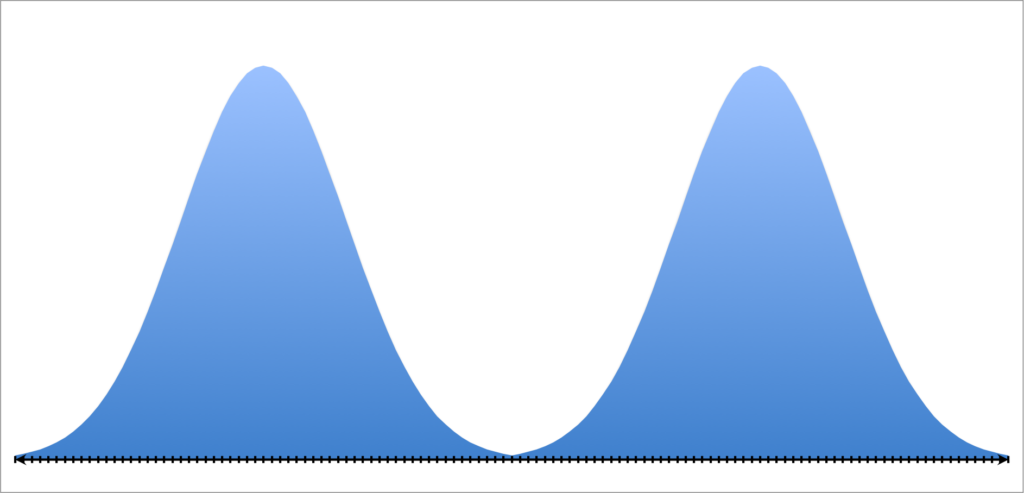
На графике представлено бимодальное распределение с 2-мя пиками. Таковая ситуация может появиться, к примеру, при голосовании на выборах.

В этом случае среднее арифметическое и медиана — это значения, находящиеся кое-где в центре и они ничего не произнесут о том, что происходит по сути и лучше сходу признать, что вы имеете дело с бимодальным распределением, сообщив о 2-ух модах.

А еще лучше поделить подборку на две группы и собрать статистические данные для каждой.

Вывод:

При выбирании способа нахождения среднего необходимо учесть наличие выбросов, также нормальность распределения значений в выборке.

Окончательный выбор меры центральной тенденции постоянно лежит на аналитике.

Как рассчитать среднее арифметическое в Excel

При работе с числовыми выражениями время от времени возникает потребность вычисления их среднего значения. В арифметике это значение именуют средним арифметическим. В Excel – табличном редакторе от Microsoft – есть возможность не вручную высчитывать его, а пользоваться особыми инструментами. В данной для нас статье как раз-таки будут представлены методы, дозволяющие выяснить и вывести число среднего арифметического.

Метод 1: обычный

Первостатейно разберем метод, как посчитать среднее арифметическое в Excel, который предполагает внедрение обычного инструмента для этого. Способ является более обычным и комфортным для использования, но у него есть и некие недочеты. Но о их позднее, а на данный момент перейдем к выполнению поставленной задачки.

1. Выделите ячейки столбца либо строчки, в которых находятся числовые значения для расчета.
2. Перейдите во вкладку «Основная».
3. На панели инструментов в группы «Редактирование» нажмите по кнопочке «Автосумма», но нажимать нужно на стрелочку рядом с ней, чтоб возник выпадающий перечень.
4. В нем для вас нужно кликнуть по пт «Среднее».

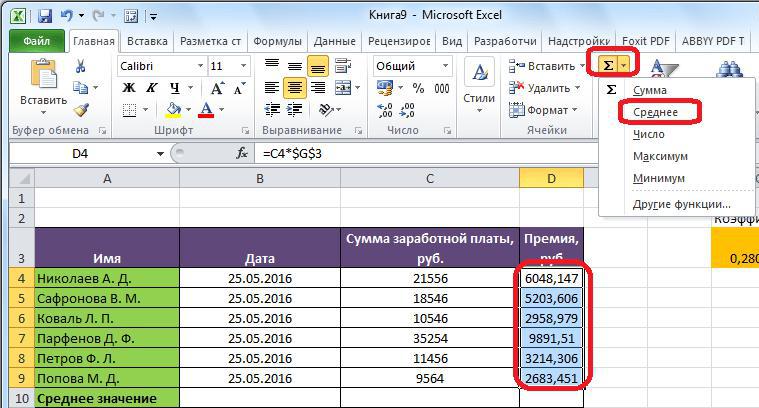
Как вы это сделаете, в ячейке рядом покажется итог расчета среднего арифметического выделенных значений. Его размещение будет зависеть от блока данных, если вы выделили строчку, то находиться итог будет справа от выделения, если столбец, снизу.

Но как было сказано ранее, у данного способа есть и недочеты. Так, у вас не получится высчитать значение из спектра ячеек, либо же ячеек, расположенных в различных местах. К примеру, если в вашей таблице смежно находятся два столбца с числовыми значениями, то, выделив их и произведя вышеперечисленные деяния, вы получите итог для всякого столбца в отдельности.

Метод 2: при помощи Мастера функций

Методов, позволяющих отыскать среднее арифметическое в Excel, существует много, и естественно, что с помощью их есть возможность обойти ограничения, предполагающие предшествующий метод. На данный момент будет поведано о произведении вычислений методом использования Мастера функций. Итак, вот что для вас нужно создать.

1. Нажав левую клавишу мыши, выделите ячейку, в которой желаете созидать итог вычислений.
2. Откройте окно Мастера функций, нажав по кнопочке «Вставить функцию», расположенной слева от строчки формул или использовав жаркие клавиши Shift+F3.
3. В показавшемся окне найдете в перечне строчку «СРЗНАЧ», выделите ее и нажмите клавишу «ОК».
4. Покажется новое окно для ввода аргументов функции. В нем вы увидите два поля: «Число1» и «Число2».
5. В 1-ое поле введите адреса ячеек, в которых размещены числовые значения для расчета. Создать это можно как вручную, так и при помощи специального инструмента. Во 2-м случае нажмите по кнопочке, расположенной в правой части поля для ввода. Окно Мастера свернется и для вас нужно будет выделить мышкой ячейки для расчета.
6. Если иной спектр ячеек с данными находится в другом месте листа, тогда укажите его в поле «Число2».
7. Проделайте ввод данных, пока не укажете все нужные.
8. Нажмите клавишу «ОК».

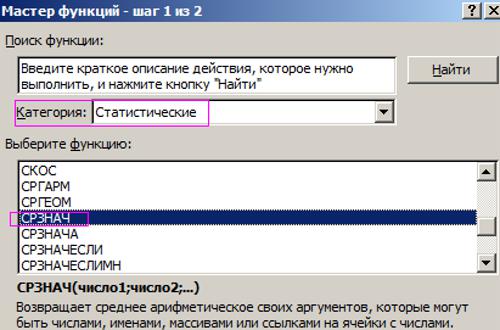
По окончании ввода окно Мастера закроется, а в ячейке, которую вы выделяли в самом начале, покажется итог вычислений. Сейчас вы понимаете 2-ой метод, как высчитать среднее арифметическое в Excel. Но далековато не крайний, потому двигаемся далее.

Метод 3: через панель формул

Данный способ, как высчитать среднее арифметическое в Excel, не много чем различается от предшествующего, но в неких вариантах он может показаться удобнее, потому его стоит разобрать. По большей части, данный метод дает только другой вариант вызова Мастера функций.

1. Перейдите на вкладку «Формулы».
2. Выделите ячейку, в которой желаете созидать итог вычислений.
3. На панели инструментов нажмите на клавишу «Остальные функции», расположенной в группе инструментов «Библиотека функций».
4. В показавшемся меню наведите курсор на пункт «Статические» и в доп перечне изберите функцию «СРЗНАЧ».

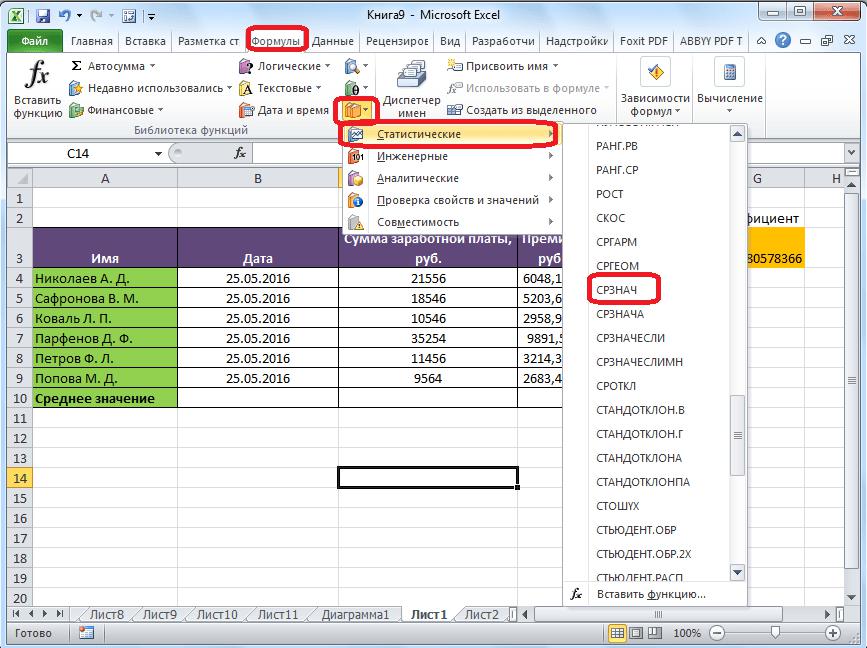
Как все деяния перечня будут выполнены, перед вами покажется окно Мастера функций, где нужно ввести аргументы. Как это созодать вы уже понимаете из предшествующего способа, все следующие деяния ничем не различаются.

Метод 4: ручной ввод функции

При желании реально избежать взаимодействия с Мастером функции, если знать формулу среднего арифметического в Excel. В неких ситуациях ручной ее ввод во много раз убыстрит процесс расчета.

Чтоб разобраться во всех аспектах, нужно поглядеть на синтаксис формулы, смотрится он последующим образом:

Из синтаксиса следует, что в аргументах функции нужно прописывать или адресок спектра ячеек, в которых находятся числа для подсчета, или конкретно сами числа для вычисления. На практике внедрение данного способа смотрится последующим образом:

Метод 5: расчет по условию

Среднее арифметическое в Excel можно посчитать и с внедрением неких критерий. Для этого применяется слегка измененная формула «СРЗНАЧЕСЛИ». Поначалу ее нужно запустить:

• выделите ячейку, в которой будет совершаться расчет;
• нажмите клавишу «вставить функцию»;
• в показавшемся окне мастера в перечне выделите строчку «срзначесли»;
• нажмите «ОК».

Опосля этого покажется окно для ввода аргументов функции. Оно весьма похоже на то, что было продемонстрировано ранее, лишь сейчас возникло доп поле – «Условие». Конкретно в него нужно вчеркивать условие. Так, введя «>1500», в расчет будут браться лишь те значения, которые больше обозначенного.

Этот метод как высчитать среднее арифметическое в Excel, непревзойденно подойдет в тех вариантах, когда вы работаете с большим спектром данных, исключение ненадобных значений из которого занимает много времени.