ПЛТ в Excel (функция)

ПЛТ в Excel (функция)

Функция ПЛТ в Excel возвращает нам размер выплаты за один период годичный ренты. Формула ПЛТ относится к особенной группе денежных функций программки и имеет особое применение в соответственных расчётах.

ПЛТ в Excel является довольно нередко применяемой функцией, что доказывается значимым количеством запросов в поисковике в Yandex и Гугл. Необходимо отметить, что группа денежных формул, к которым относится и ПЛТ, в Excel употребляются всё же еще пореже функций обработки текста, также числовых формул. Разъясняется это просто — для разных денежных вычислений есть спец программки, вроде 1С:Предприятие и иных.

Тем не наименее, и в Excel можно делать подобные расчёты, что в особенности принципиально в тех вариантах, когда требуется создать что-то необычное, построенное на собственной своей логике, а программера под рукою нет. Давайте разглядим функцию ПЛТ, которая в Excel применяется для расчёта суммы аннуитетного платежа.

Синтаксис функции ПЛТ

Функция ПЛТ воспринимает целых 5 характеристик, которые используются для указания разных атрибутов расчёта размера повторяющегося платежа. Ниже рассмотрено предназначение всякого аргумента функции.

В обобщённом виде функция ПЛТ смотрится вот так:
ПЛТ(ставка;кпер;плт;[бс];[тип])

Видите ли, 1-ые три аргумента у функции необходимо задавать непременно, а другие два можно опустить, на что указывают квадратные скобки, в которые заключены аргументы. Предназначение аргументов, невзирая на непонятные наименования (что типично для группы денежных формул Excel), уяснить нетрудно. Читайте перечень ниже.

• Ставка
  Это неотклонимый аргумент, который задаёт процентную ставку по взятой ссуде (кредиту). Невзирая на то, что значение задаётся в процентах, знак процента можно не указывать.
• К_пер
  Коэффициент К описывает общее число выплат по ссуде и также является неотклонимым аргументом.
• П_с
  Приведенная к текущему моменту стоимость либо общая сумма, которая на текущий момент равноценна ряду будущих платежей, именуемая также главный суммой.
• Б_с
  Этот аргумент указывает, какой должен быть остаток долга опосля выплаты крайнего платежа. Если аргумент не указан, то считается что остаток должен быть равен нулю (в денежных определениях: будущая стоимость займа равна нулю), другими словами долг гасится на сто процентов.
• Тип
  Когда обязана выполняться выплата: в начале периода (указать 1) либо в конце (указать 0 либо можно совершенно пропустить данный аргумент, потому что ноль является значением по дефлоту).

Стоит держать в голове, что функция ПЛТ предназначается для расчёта главных платежей и выплату процентов по взятой ссуде (кредиту), но не учитывает разные доп платежи, которые могут быть в таковых вариантах (разные комиссии, штрафы за просрочку, налоги и прочее — банки, как понятно, очень изобретательны).

Также удостоверьтесь, что Вы поочередны в выборе единиц измерения для задания аргументов «ставка» и «кпер». Если вы делаете каждомесячные выплаты по четырехгодичному займу из расчета 12 процентов годичных, то используйте значения 12%/12 для задания аргумента «ставка» и 4*12 для задания аргумента «кпер». Если вы делаете каждогодние платежи по тому же займу, то используйте 12 процентов для задания аргумента «ставка» и 4 для задания аргумента «кпер».

Для нахождения общей суммы, выплачиваемой в протяжении интервала выплат, помножьте возвращаемое функцией ПЛТ значение на «кпер».

Доборная информация по функции ПЛТ есть в обычной справке Excel, прочесть которую можно как в самой программке, так и опосля данной статьи в формате PDF.

ПЛТ в Excel на примерах

Сейчас поглядим, как ПЛТ в Excel можно применить на практике. Для этого разглядим пример использования данной формулы. Также опосля статьи прикреплён файл Excel, в котором данный пример Вы сможете протестировать без помощи других для различных характеристик (скачайте файл и запустите в программке).

Для начала разглядим пример расчёта размера аннуитетного платежа по кредиту. Есть последующие входные данные:

• 8% — Годичная процентная ставка (ячейка A5);
• 10 — Количество месяцев платежей (ячейка A6);
• 10000 (рублей, к примеру) — Сумма кредита (ячейка A7);

В итоге формула будет иметь последующий вид: «=ПЛТ(A5/12;A6;A7)», а в итоге мы получим размер каждомесячного платежа равным -1 037,03 ₽.

Тот же пример рассмотрен на видео. Также функцию ПЛТ можно применять для расчёта платежей по вкладу с целью получить подходящую сумму через определённное количество лет ожидания. Другими словами формулу ПЛТ можно применять и в оборотном направлении. Оба примера есть в прикреплённом файле и в маленьком видеоролике.

Если желаете знать не только лишь отдельные функции программки, да и совершенно осознавать, как работает Excel, то советуем направить внимание на наш спецкурс, познакомиться с примерами уроков которого можно тут.

Придумаете увлекательный пример внедрения ПЛТ — опубликуйте его в комментах в помощь иным нашим читателям, изучающим Excel. Но, просьба не писать в комментах вопросцы вида «как создать это либо то», так как у нас нет времени на подобные ответы.

Глядеть видео
ПЛТ в Excel (функция)

Прикреплённые документы

Вы сможете просмотреть хоть какой прикреплённый документ в виде PDF файла. Все документы открываются во всплывающем окне, потому для закрытия документа пожалуйста не используйте клавишу «Вспять» браузера.

• Справка по функции ПЛТ в Excel.pdf

Файлы для загрузки

Вы сможете скачать прикреплённые ниже файлы для ознакомления. Обычно тут располагаются разные документы, также остальные файлы, имеющие конкретное отношение к данной публикации.

Функция плт в excel пример

3. Проверить свои познания по контрольным вопросцам и сдать лабораторную работу.

Главные сведения по теме:

Финансовая функция ПЛТ

Лист1 в книжке ФИНАНСОВЫЙ АНАЛИЗ переименуйте в ПЛТ. Все упражнения в данной лабораторной работе делайте на листе ПЛТ.

Разглядим пример расчета 30-летней ипотечной ссуды со ставкой 8% годичных при исходном взносе 20% и каждомесячной (каждогодней) выплате при помощи функции ПЛТ.

Для приведенного на рис.4.1.1 ипотечного расчета в ячейки введены формулы, показанные на рис. 4.1.2.

Рис. 4.1.1 Расчет ипотечной ссуды

Введите выставленные на рис. 4.1.2. данные на лист ПЛТ и сравните приобретенный итог с данными на рис. 4.1.1.

Рис. 4.1.2 Формулы для расчета ипотечной ссуды

Функция ПЛТ вычисляет величину неизменной повторяющейся выплаты ренты (к примеру, постоянных платежей по займу) при неизменном процентной ставке.

Синтаксис: ПЛТ(ставка; кпер; пс; бс; тип).

ставка—процентная ставка по ссуде, кпер — общее число выплат по ссуде, пс — приведенная к текущему моменту стоимость, либо общая сумма, которая на текущий момент равноценна ряду будущих платежей, именуемая также главный суммой, бс — требуемое значение будущей цены, либо остатка средств опосля крайней выплаты. Если аргумент бс опущен, то он полагается равным 0 (нулю), т. е. для займа, к примеру, значение бс равно 0, Тип — число 0 (нуль) либо 1, обозначающее, когда обязана выполняться выплата.

Если бс = 0 и тип = 0, то функция ПЛТ вычисляет по формуле (1):

Отметим, что весьма принципиально быть поочередным в выборе единиц измерения для задания аргументов ставка и КПЕР. К примеру, если вы делаете каждомесячные выплаты по четырехгодичному займу из расчета 12% годичных, то для задания аргумента ставка используйте 12%/12, а для задания аргумента КПЕР — 4*12. Если вы делаете каждогодние платежи по тому же займу, то для задания аргумента ставка используйте 12%, а для задания аргумента КПЕР — 4.

Для нахождения общей суммы, выплачиваемой в протяжении интервала выплат, помножьте возвращаемое функцией ПЛТ значение на величину КПЕР. Интервал выплат — это последовательность неизменных валютных платежей, осуществляемых за непрерывный период. К примеру, заем под кар либо заклад являются интервалами выплат. В функциях, связанных с интервалами выплат, выплачиваемые вами средства, такие как депозит на скопление, представляются отрицательным числом, а средства, которые вы получаете, такие как чеки на дивиденды, представляются положительным числом. К примеру, депозит в банк на сумму 1000 руб. представляется аргументом -1000, если вы вкладчик, и аргументом 1000, если вы — пpeдставитель банка.

Задание

Высчитайте 5-летнюю ипотечную ссуду в размере 500 тыс. руб. со ставкой 18% годичных при исходном взносе 20% и каждомесячной (каждогодней) выплате.

Задание делайте в новейшей книжке Задания.xls , Лист1 переименуйте в ПЛТ.

Порядок отчета лабораторной работы:

При отчете лабораторной работы нужно:

1) Показать выполненные упражнения, описанные в методических указаниях;

2) Показать выполненное задание, откомментировать порядок его выполнения и разъяснить приобретенные результаты;

3) Ответить на контрольные вопросцы.

Контрольные вопросцы:

1) Какие задачки дозволяет решать Microsoft Excel?

2) Как вызывается подходящая функция?

3) Какие группы функций Для вас известны?

4) Что дозволяет вычислить функция ПЛТ?

5) Какие характеристики у функции ПЛТ?

Перечень литературы:

1. Гарнаев А.Ю. Внедрение MS Excel и VBA в экономике и денег.-СПб.: БХВ- Санкт-Петербург, 1999.- 336 с., ил.

2. Информатика. Серия «Учебники, учебные пособия». И57 // Под ред. П.П. Беленького. – Ростов на дону н/Д: Феникс, 2002. 448с.

3. А.В. Могилев, Пак, Хеннер. Информатика. М: Изд. центр «Академия», 2000г.- 816 с.

Лабораторная работа №2

Организация стока поверхностных вод: Наибольшее количество воды на земном шаре испаряется с поверхности морей и океанов (88‰).

Папиллярные узоры пальцев рук — маркер спортивных возможностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не меняются в течение жизни.

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от нрава защищаемого.

Функция ПЛТ в Excel

Хороший денек, почетаемые подписчики и читатели блога. Весьма много поступает вопросцев по поводу «кредитных калькуляторов» как их сделать в Excel и использовать на практике.

Вправду в Excel есть мало нужный набор функций. К примеру, ПЛТ (платёж). Другими словами мы должны выяснить сумму кредита и минусовать с неё платёж первого периода, считать процент, минусовать процент последующего платежа и т.д. Условие одно — платежи должны быть равными.

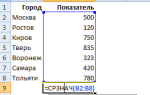
Давайте попробуем пользоваться данной функцией. Построим маленькую таблицу:

Позовём нашу функцию и поглядим на её аргументы.

Аргументов много (в принципе любой аргумент ПЛТ это отдельная функция):

Ставка — это ставка для периода (если ставка квартальная то 13% я делю на 4 квартала, если ставка месячная то 13% делим на 12 и т.д), в нашем случае берём конкретно 2-ой вариант.

Кпер — количество периодов для выплат по займу.

Пс — текущая стоимость займа (в нашем случае 700000 рублей).

Бс — будущая стоимость займа.

Тип — воспринимает значения 0 либо 1 в зависимости от платежа сначала либо в в конце периода (в конце 0, в начале 1).

Заполним аргументы функции нашими данными.

В итоге получим. Оставим «Бс» и «Тип» пустыми, они воспримут значение 0, он то нам и нужен!

Итог со знаком минус — мы теряем эти средства. Если охото созидать положительную сумму — сумму кредита необходимо ввести со знаком минус (-700000).

Итог налицо! Это будет наш каждомесячный платёж. Несложно посчитать, что за весь период мы выплатим банку 750365,12 рублей.

Идём далее, давайте проведём маленький анализ по процентной ставке и сроку кредита. Возьмём ставки — 13%, 15%, 19% и 25%. Периоды кредитования — 12, 24, 36, 48 и 60 месяцев.

Из формул массивов мы знаем, что можно множить спектр на спектр, но нам также необходимо учитывать и первоначальную сумму кредита. Потому воспользуемся возможностью программки «Анализ что если?». За ранее выделим всю таблицу данных (от А8 до F12):

• перебегаем на вкладку «Данные»;
• в блоке клавиш «Работа с данными» жмем клавишу «Анализ что если?»;
• избираем «Таблица данных»

Сейчас необходимо указать куда (в какие ячейки подставлять) наши показания по количеству месяцев (столбцы) и процентную ставку (строчки). Укажем надлежащие ячейки — B4 и B5. Жмем «ОК»

Остается понаблюдать за результатом.

Как видно из строчки формул — возникли фигурные скобки (признак массива) и функция ТАБЛИЦА. Не отыскиваете её просто так, она покажется лишь при использовании «Таблицы данных» из «Анализ «что если?».

Готово, наш маленький калькулятор готов. Можно будет при помощи пользовательских форматов дописать «месяцев» к нашим периодам, но это как раз можно почитать в предшествующей статье.

Обычная математика, Excel. Как минимум. Но не только лишь.

Странички

пятница, 5 ноября 2010 г.

Денежные функции Excel

В предшествующей заметке была рассмотрена техно сторона расчета кредита.

Но если фактически, то запускаем Excel, там много денежных функций и высчитать платеж по кредиту не неувязка.

Кпер — число периодов платежей по кредиту (каждый месяц на 5 лет можем написать 5*12).
Ставка — процентная ставка (если 17% годичных, то пишем либо 17%/12 либо 0,17/12, но никак не 17 просто).
Плт — платеж, производимый в любой период, состоит из основного платежа и платежа по процентам.
Пс — сумма на текущий момент.
Бс — будущая стоимость.
Тип — число 0 — оплата (выдача денег по какому-нибудь обязательству) в конце периода, число 1 — оплата (выдача денег по какому-нибудь обязательству) в начале периода (по дефлоту — 0).

Эти переменные могут быть положительными либо отрицательными, в зависимости от того получаем мы средства либо отдаем.

Используя функцию ПЛТ(ставка; кпер; пс; [бс]; [тип]) , рассчитаем сумму каждомесячного платежа при сумме кредита 50 000 руб. сроком на 2 года по 17% годичных.
Аргументы в квадратных скобках необязательные.

Пишем в ячейке =ПЛТ(17%/12; 2*12; 50000) . Получаем -2 472,11р.
Минус гласит, что это наши расходы.

Остальные функции смотрятся так:

КПЕР(ставка; плт; пс; [бс]; [тип]) — вычисляет количество периодов платежей

ПС(ставка; кпер; плт; [бс]; [тип]) — сумма средств на данный момент

БС(ставка; кпер; плт; [пс]; [тип]) — сумма средств спустя определенное (кпер) время

Разглядим применение этих функций.

Пример 1. Пусть ставка кредита 17% годичных, сумма 100 000 руб. и мы можем выплачивать по 5 000 каждый месяц. Найти за сколько периодов мы погасим кредит поможет функция КПЕР() .

Пишем минус 5000, т.к. отдаем средства.
Получаем примерно 23,68 периодов, т.е. фактически 2 года.
—————————————————————
Пример 2. На какую сумму можно взять кредит, если ставка 17% годичных и выплачивать мы можем по 10 000 руб. в протяжении 2-х лет (24 периода). Используем ПС() .

Получаем примерно 202 256 руб.
—————————————————————
Пример 3. Какую сумму кредита можно взять под 17% годичных с каждомесячным начислением процентов, если выплачивать мы можем в протяжении 2-х лет (24 периода) и в итоге готовы выплатить 300 000 руб. Используем ПС() .

Тут у нас нет переменной плт , зато есть переменная бс . Ее пишем с минусом, т.к. отдаем эту сумму.
Получаем примерно 214 041 руб.
—————————————————————
Пример 4. Желаем создать вклад под 15% годичных с каждомесячным начислением процентов на сумму 100 000 руб. и на 3 года (36 периодов). Используем БС( ).

Тут переменная пс равна -100 000 минус обозначает то, что мы отдаем средства.
Итог 156 394 руб.
—————————————————————
Пример 5. Пусть те же условия, что и в примере выше, лишь каждый месяц мы будем пополнять счет еще на 1 000 руб.

Т.к. снимаем средства, то переменная плт с плюсом.
Итог 111 279 руб.
—————————————————————
Пример 7. Пусть желаем взять кредит в 100 000 рублей на 2 года, выплачивать можем по 5 000 руб. каждый месяц. Какая ставка нам подступает. Используем функцию СТАВКА() .

Итог 1,51308%, но это в месяц. Умножим на 12, получим 18,157%.

PI в Excel

Пи — неизменное значение в математике, которое употребляется для вычислений, где в математике мы имеем значение до 2-ух десятичных символов, но в Excel у нас есть интегрированный Функция PI () который сохраняет четкое значение до 15 символов опосля запятой, эта функция употребляется в разных остальных формулах для последующих вычислений.

Синтаксис

В тот момент, когда вы примените функцию PI, она возвратит значение, примерно равное 15 цифрам, другими словами 3,141592653589790.

Как вставить формулу PI в Excel?

Так как у PI нет аргументов, разрешите мне показать для вас, как вставить формулу PI в Excel.

В хоть какой ячейке вашего листа Excel откройте функцию PI и просто закройте скобки; тут у нас будет значение PI.

Значение PI является иррациональным числом, потому десятичных символов нет. Excel может показывать до 30 десятичных символов, но неважно какая цифра опосля 14 десятичных символов будет отображаться как ноль.

Как применять формулу PI в Excel? (с примерами)

Пример # 1

Сейчас разглядим пример определения цены тортика за дюйм. Когда я задал вопрос о тортике для новогодней вечеринки, я получил две цитаты из магазина.

• Два килограмма тортика размером 10 см обойдутся мне в 500 рупий.
• Пятикилограммовый тортик, который составляет 15 см, мне обойдется в 600 рупий.

Сейчас желаю выяснить стоимость дюйма тортика и заказать самый дешевенький тортик на вечеринку.

Размер тортика — это не что другое, как поперечник круга. Радиус круга постоянно равен половине поперечника. Итак, получите Радиус тортика, разделив поперечник на 2.

Итак, мы получили радиус 5 для тортика поперечником 10 дюймов.

Перетащите формулу в ячейку C3.

Сейчас нам необходимо вычислить площадь круга (AOC). Формула для расчета AOC смотрится последующим образом.

AOC = PI * R 2

R = радиус круга.

Применим формулу, чтоб отыскать AOC. AOC — это значение ПИ, умноженное на квадрат радиуса.

АОС обоих тортов приводится ниже.

Сейчас посчитайте стоимость за дюйм. Формула: Стоимость / AOC.

Стоимость за дюйм для обоих тортов последующая.

Из приведенного выше расчета лучше приобрести тортик на 15 дюймов по стоимости 4,53 рупии за дюйм.

Таковым образом, мы можем применять PI для расчета цены и принятия решения.

Два обычных метода создать формулу расчета сложных процентов в Excel

Приветствую! Не понимаю как Вы, а я люблю все за всеми перепроверять. Потому и свои расчеты по инвестициям себе веду в Excel на домашнем компе. Ну, не доверяю я всем сиим онлайн-калькуляторам в Сети! Ну и совершенно, когда вводишь все числа руками, управление личными деньгами становится каким-то наиболее осознанным, что ли…

Сейчас я расскажу, как в экселе создать формулу с процентами по вкладу (либо хоть какому другому вкладывательному инструменту). Проценты будем учесть, естественно, не обыкновенные, а сложные. На всякий вариант: это когда уже начисленный процент Вы не снимаете, а сходу присоединяете к сумме вклада.

Разглядим самый обычной вариант – один раз вложили куда-нибудь средства, и они там потихоньку «плодятся» без допвливаний. Простой расчет в Excel можно создать 2-мя методами: вручную и при помощи специальной функции.

Вручную

Для этого нам пригодится вот эта формула:

• ФК – это наш финишный капитал либо конечный итог. В общем, та сумма, которую мы получим на финише с учетом накопительного эффекта сложных процентов. К слову, весьма настраивает на постоянные инвестиции! Полезно своими очами узреть, в какие суммы преобразуются даже маленькие вложения через 5,10 либо 20 лет
• Ко – это исходный капитал, который мы инвестируем на долгий срок по принципу «вложили – и не трогаем»
• R – годичная процентная ставка в толиках (к примеру, 12% годичных будут смотреться как 0,12)
• m – период реинвестирования в месяцах. Проще говоря, как нередко будут начисляться проценты по вкладу и плюсоваться к общей сумме. Если ставка по банковскому вкладу начисляется любой месяц, то m будет равно 1, если ежеквартально – то 3, если раз в году – то 12
• n – количество периодов реинвестирования. К примеру, если проценты реинвестируются раз в месяц, то за год выходит 12 периодов реинвестирования, а за 5 лет n будет равно 60

Сейчас осталось сформировать простенькую табличку в Excel: из 5 строчек и 2-ух столбцов.

• Строка №1 – исходный капитал (Ко)
• Строка №2 – годичная процентная ставка ( R )
• Строка №3 – период реинвестирования (m)
• Строка №4 – количество периодов (n)
• Строка №5 — финишный размер капитала (ФК)

1-ые четыре строки мы заполняем вручную. В каждой из их формат будет «общим», и лишь годичную процентную ставку необходимо прописывать в формате «процентный».

А далее в ячейке с финишным капиталом забиваем формулу (по номерам строчек): =№1*(1+(№2*№3/12))^№4. На всякий вариант, значок «^» в Excel находится так: «Вставка» — «Знак» — «^» — «Вставить», либо при помощи композиции кнопок «Shift+6» в британской раскладке.

Все, простая таблица в Excel готова! Сейчас можно «играть» с размером исходного капитала, годичный ставкой и количеством периодов. И созидать, как вырастает (либо миниатюризируется) величина финишного капитала.

При помощи специальной функции

Excel так всепригодная программка, что потенциальную доходность по вкладу нам поможет высчитать особая функция. Для начала заходим на вкладку «Формула» (в самом верху странички) и кликаем на знак fx либо «Вставить функцию» (в левом верхнем углу).

Здесь же раскрывается окно «Мастер функций». В строке поиска вводим БС (для тех, кто не в курсе, БС – это будущая стоимость) и жмем Enter. Выпадает целый перечень непонятных заглавий – мы избираем все этот же БС. Либо можно просто избрать вручную из группы «Денежные».

В итоге на дисплее возникает табличка, которую необходимо заполнить данными из формулы, которую я приводил выше.

• Поле «Ставка» – все та же годичная процентная ставка в толиках. Если проценты начисляются каждый месяц, то делим годичный процент на 12, если ежеквартально – то на 4 и т.д.
• Поле «Кпер» – количество лет инвестирования. Если выплаты выполняются раз в месяц, то умножаем количество лет на 12 и т.д.
• Поле «Плт» — оставляем пустым
• Поле «ПС» — исходный размер вклада. Тут его необходимо записать со знаком минус, потому что свои «кровные» мы отдаем, а не получаем
• Поле «Тип» учитывает метод выплаты процентом по вкладу
• Если проценты выплачиваются в конце срока деяния вклада, то ставим «0» либо оставляем поле пустым
• Если в начале срока – то «1».

Кликаем на ОК – и вуаля! Размер нашего грядущего капитала уже отображен в ячейке!

Тестовый пример

Для примера я брал сумму в $10 000, размещенную на вкладе со ставкой 6% годичных сроком на 4 года.

Оба варианта дали один и этот же итог – через 4 года мой вклад вырастет до $12 704,89. Это, естественно, при условии, что капитализация процентов будет каждомесячной.

Могу сказать, что 1-ый метод расчета отбирает чуток больше времени, зато он наглядней и «вдумчивей».

К слову, наиболее сложными формулами можно рассчитывать и остальные характеристики инвестиций: доходность вклада с постоянным пополнением, переплату по кредиту, годичную процентную ставку, размер исходного капитала и много чего же еще.

Если вы желаете, чтоб я поведал как рассчитывается неважно какая из приведенных выше функций — оставляйте свои пожелания в комментах под данной статьей. А при помощи чего же Вы обычно считаете сложные проценты?

Подписывайтесь на обновления и не запамятовывайте делиться постами в соц сетях!