5 методов расчета значений линейного тренда в MS Excel
Это 1-ая статья из серии «Как без помощи других высчитать прогноз продаж с учетом роста и сезонности», из которой вы узнаете о 5 методах расчета значений линейного тренда в Excel.
Для того, чтоб легче было научиться предсказывать реализации с учетом роста и сезонности, я разбил 1 огромную статью о расчете прогноза на 3 части:
-
- Расчет значений тренда (разглядим на примере Линейного тренда в данной нам статье);
- Расчет сезонности;
- Расчет прогноза;
Опосля исследования данного материала вы можете избрать лучший метод расчета значений линейного тренда, который будет комфортен для решения вашей задачки, а в последствии, и для расчета прогноза более комфортным вам методом.
Линейный тренд отлично использовать для временного ряда, данные которого растут либо убывают с неизменной скоростью.
Разглядим линейный тренд на примере расчета прогноза продаж в Excel по месяцам.
Временной ряд реализации по месяцам (см. вложенный файл).
В этом временном ряду у нас есть 2 переменных:
- Время — месяцы;
- Объём продаж;
Уравнение линейного тренда y(x)=a+bx, где
y — это объёмы продаж
x — номер периода (порядковый номер месяца)
a – точка пересечения с осью y на графике (малый уровень);
b – это значение, на которое возрастает последующее значение временного ряда;
1-й метод расчета значений линейного тренда в Excel при помощи графика

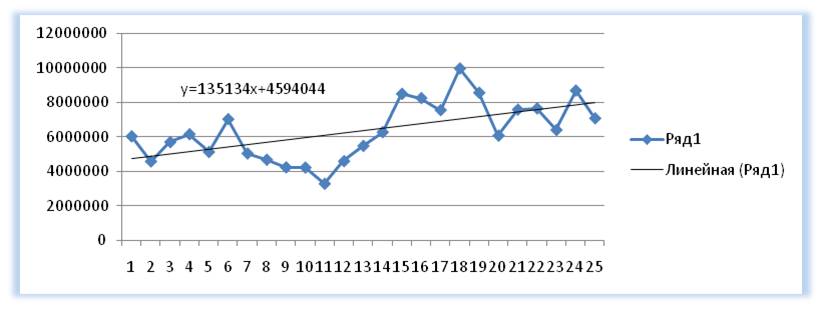
Выделяем анализируемый объём продаж и строим график, где по оси Х — наш временной ряд (1, 2, 3… — январь, февраль, март …), по оси У — объёмы продаж. Добавляем линию тренда и уравнение тренда на график. Получаем уравнение тренда y=135134x+4594044
Для прогнозирования нам нужно высчитать значения линейного тренда, как для анализируемых значений, так и для будущих периодов.
При расчете значений линейного тренде нам будут известны:
- Время — значение по оси Х;
- Значение «a» и «b» уравнения линейного тренда y(x)=a+bx;
Рассчитываем значения тренда для всякого периода времени от 1 до 25, также для будущих периодов с 26 месяца до 36.
К примеру, для 26 месяца значение тренда рассчитывается по последующей схеме: в уравнение подставляем x=26 и получаем y=135134*26+4594044=8107551
27-го y=135134*27+4594044=8242686
2-й метод расчета значений линейного тренда в Excel — функция ЛИНЕЙН
1. Рассчитаем коэффициенты линейного тренда при помощи обычной функции Excel:
=ЛИНЕЙН(известные значения y, известные значения x, константа, статистика)
Для расчета коэффициентов в формулу вводим
известные значения y (объёмы продаж за периоды),
известные значения x (номера периодов),
заместо константы ставим 1,
заместо статистики 0,
Получаем 135135 — значение (b) линейного тренда y=a+bx;
Для того чтоб Excel высчитал сходу 2 коэффициента (a) и (b) линейного тренда y=a+bx, нужно
- установить курсор в ячейку с формулой и выделить соседнюю справа, как на рисунке;

- жмем кнопку F2, а потом сразу — клавиши CTRL + SHIFT + ВВОД.
- известные значения y — это объёмы продаж за анализируемый период (закрепляем спектр в формуле, выделяем ссылку и жмем F4);
- известные значения x — это номера периодов x для узнаваемых значений объёмов продаж y;
- новейшие значения x — это номера периодов, для которых мы желаем высчитать значения линейного тренда;
- константа — ставим 1, нужно для того, чтоб значения тренда рассчитывались с учетом коэффицента (a) для линейного тренда y=a+bx;
- рассчитаем коэффициенты сезонности,очищенные от роста и выровненные;
- создадим прогноз;
- Novo Forecast Lite — автоматический расчет прогноза в Excel .
- 4analytics — ABC-XYZ-анализ и анализ выбросов в Excel.
- Qlik Sense Desktop и QlikView Personal Edition — BI-системы для анализа и визуализации данных.
- Novo Forecast PRO — прогнозирование в Excel для огромных массивов данных.
- Коэффициент a рассчитывается как Yср.-bXср. (Yср. и Xср. – среднее арифметическое чисел из выборок узнаваемых значений y и x соответственно).
- Коэффициент b определяется по формуле:
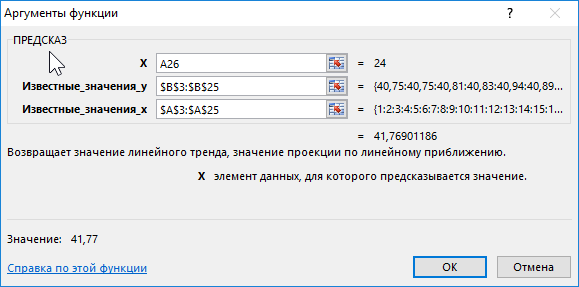
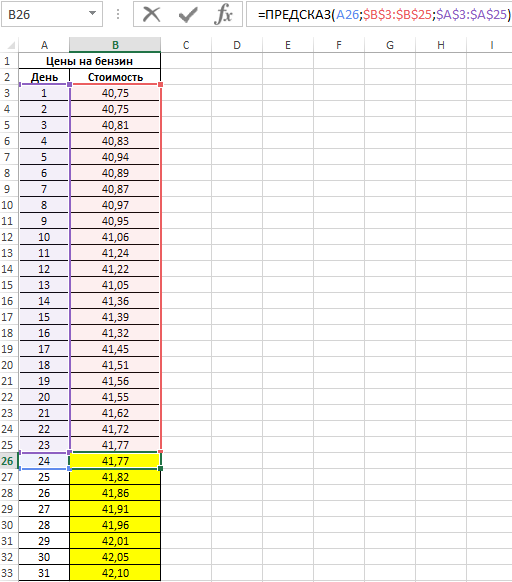
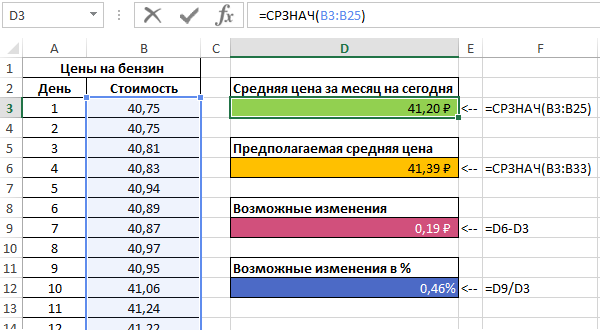
- A26:A33 – спектр ячеек с номерами дней месяца, для которых данные о цены бензина еще не определены;
- B3:B25 – спектр ячеек, содержащих данные о цены бензина за крайние 23 денька;
- A3:A25 – спектр ячеек с номерами дней, для которых уже известна стоимость бензина.
- Изменение нашей пронозируемой величины (к примеру, продаж) подчиняется некому закону. Иными словами, в временном ряде можно проследить некоторую тенденцию. В арифметике таковая тенденция именуется трендом.
- Изменение значений в временном ряде может зависить от промежутка времени. Иными словами, при построении модели нужно будет учитывать коэффициент сезонности. К примеру, реализации арбузов в январе и августе не могут быть схожими, т.к. это сезонный продукт и в летнюю пору реализации существенно выше.
- Изменение значений в временном ряде временами повторяется, т.е. наблюдается некая цикличность.
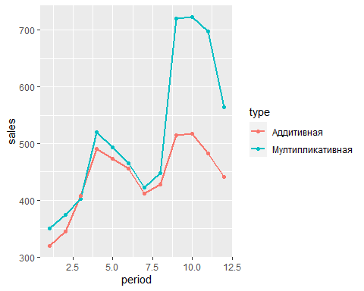
- Аддитивная модель: Уровень временного ряда = Тренд + Сезонность + Случайные отличия
- Мультипликативная модель: Уровень временного ряда = Тренд X Сезонность X Случайные отличия
- Смешанная модель: Уровень временного ряда = Тренд X Сезонность + Случайные отличия
- с внедрением линейного тренда
- с внедрением полиномиального тренда
- y — значения продаж
- x — номер периода
- a — коэффициент наклона прямой тренда
- b — вольный член тренда
- Выделяем две ячейки рядом
- Ставим курсор в поле формул и вводим формулу =ЛИНЕЙН(C4:C27;B4:B27)
- Жмем Ctrl+Shift+Enter, чтоб активировать формулу массива
- Ставим в ячейку F4 курсор и вводим формулу =ИНДЕКС(ЛИНЕЙН($C$4:$C$27;$B$4:$B$27^<1;2;3;4>);1;1). Функция ЛИНЕЙН дозволяет произвести расчет коэффициентов, а при помощи функции ИНДЕКС мы вытаскиваем подходящий нам коэффициент. В этом случае за выбор коэффициента отвечает самый крайний аргумент. У нас стоит 1 — это коэффициент при самой высочайшей степени (т.е. при 4 степени, коэффициент). К слову, выяснить о самых нужных математических формулах Excel можно в нашем бесплатном гайде «Математические функции Excel».
- Аналогично прописываем формулу =ИНДЕКС(ЛИНЕЙН($C$4:$C$27;$B$4:$B$27^<1;2;3;4>);1;2) в ячейке ниже.
- Делаем такие же деяния, пока не найдем все коэффициенты.
- Выделяем столбец с продажами
- Избираем «Вставка» → «График» → «Точечный» → «Точечная диаграмма»
- Жмем на всякую точку графика правой клавишей мыши и избираем «Добавить линию тренда»
- В открывшемся справа меню избираем «Полиномиальная модель», меняем степень на 4 и ставим галочку на «Демонстрировать уравнение на диаграмме»
- Вы сможете вывести коэффициент на график, поставив галочку «Поместить на диаграмму величину достоверности аппроксимации»
- Вы сможете высчитать коэффициент R^2 без помощи других по формуле =ИНДЕКС(ЛИНЕЙН($C$4:$C$27;$B$4:$B$27^<1;2;3;4>;;1);3;1)
Получаем 135135, 4594044 — значение (b) и (a) линейного тренда y=a+bx;
2. Рассчитаем значения линейного тренда при помощи приобретенных коэффициентов . Подставляем в уравнение y=135134*x+4594044 номера периодов — x, для которых желаем высчитать значения линейного тренда.
2-й метод поточнее, чем 1-ый, т.к. коэффициенты тренда мы получаем без округления, также резвее.
3-й метод расчета значений линейного тренда в Excel — функция ТЕНДЕНЦИЯ
Рассчитаем значения линейного тренда при помощи обычной функции Excel:
=ТЕНДЕНЦИЯ(известные значения y; известные значения x; новейшие значения x; конста)
Подставляем в формулу
Для того чтоб высчитать значения тренда для всего временного спектра, в «новейшие значения x» вводим спектр значений X, выделяем спектр ячеек равный спектру со значениями X с формулой в первой ячейке и жмем кнопку F2, а потом — клавиши CTRL + SHIFT + ВВОД.
4-й метод расчета значений линейного тренда в Excel — функция ПРЕДСКАЗ
Рассчитаем значения линейного тренда при помощи обычной функции Excel:
=ПРЕДСКАЗ(x; известные значения y; известные значения x)
Заместо X поставляем номер периода, для которого рассчитываем значение тренда.
Заместо «известные значения y» — объёмы продаж за анализируемый период (закрепляем спектр в формуле, выделяем ссылку и жмем F4);
«известные значения x» — это номера периодов для всякого выделенного объёма продаж.
3-й и 4-й метод расчета значений линейного тренда резвее, чем 1 и 2-й, но с его помощью нереально управлять коэффициентами тренда, как описано в статье «О линейном тренде».
5-й метод расчета значений линейного тренда в Excel — Forecast4AC PRO
2. Заходим в меню программки и жмем «Start_Forecast». Значения линейного тренда рассчитаны.
Для расчета прогноза осталось применить к значениям трендов будущих периодов коэффициенты сезонности, и прогноз продаж с учетом роста и сезонности готов.
В последующих статье «Как без помощи других создать прогноз продаж с учетом роста и сезонности» мы:
О том, что еще принципиально знать о линейном тренде, вы сможете выяснить в статье «Что принципиально знать о линейном тренде».
Четких для вас прогнозов!
Присоединяйтесь к нам!
Скачивайте бесплатные приложения для прогнозирования и бизнес-анализа:

Тестируйте способности платных решений:
Получите 10 советов по увеличению точности прогнозов до 90% и выше.
Функция ПРЕДСКАЗ для прогнозирования будущих значений в Excel
Функция ПРЕДСКАЗ в Excel дозволяет с некой степенью точности предсказать будущие значения на базе имеющихся числовых значений, и возвращает надлежащие величины. К примеру, некий объект характеризуется свойством, значение которого меняется со временем. Такие конфигурации могут быть зафиксированы опытным методом, в итоге чего же будет составлена таблица узнаваемых значений x и соответственных им значений y, где x – единица измерения времени, а y – численная черта характеристики. При помощи функции ПРЕДСКАЗ можно представить следующие значения y для новейших значений x.
Примеры использования функции ПРЕДСКАЗ в Excel
Функция ПРЕДСКАЗ употребляет способ линейной регрессии, а ее уравнение имеет вид y=ax+b, где:
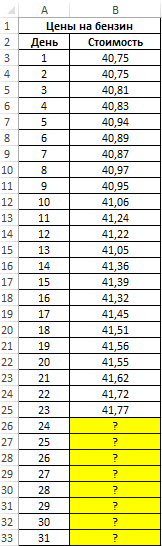
Пример 1. В таблице приведены данные о ценах на бензин за 23 денька текущего месяца. Согласно прогнозам профессионалов, средняя стоимость 1 л бензина в текущем месяце не превзойдет 41,5 рубля. Спрогнозировать стоимость бензина на оставшиеся деньки месяца, сопоставить рассчитанное среднее значение с предсказанным спецами.
Вид начальной таблицы данных:

Чтоб найти предполагаемую стоимость бензина на оставшиеся деньки используем последующую функцию (как формулу массива):


Рассчитаем среднюю стоимость 1 л бензина на основании имеющихся и расчетных данных при помощи функции:

Можно прийти к выводу о том, что если тенденция конфигурации цен на бензин сохранится, пророчества профессионалов относительно средней цены реализуются.
Анализ прогноза спроса продукции в Excel по функции ПРЕДСКАЗ
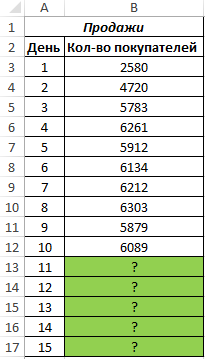
Пример 2. Компания не так давно представила новейший продукт. С момента вывода на рынок раз в день ведется учет количества клиентов, купивших этот продукт. Представить, каким будет спрос в протяжении 5 следующих дней.
Вид начальной таблицы данных:

Как видно, в 1-ые деньки спрос был маленьким, потом он рос довольно большенными темпами, а в протяжении крайних 3-х дней изменялся некординально. Это свидетельствует о том, что главным фактором роста продаж сейчас является не расширение базы клиентов, а развитие продаж с неизменными клиентами. В таковых вариантах советуют употреблять не линейную регрессию, а логарифмический тренд, чтоб результаты прогнозов были наиболее точными.
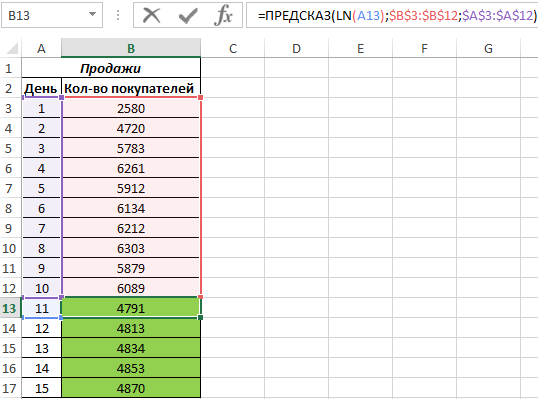
Рассчитаем значения логарифмического тренда при помощи функции ПРЕДСКАЗ последующим методом:
Как видно, в качестве первого аргумента представлен массив натуральных логарифмов следующих номеров дней. Таковым образом получаем функцию логарифмического тренда, которая записывается как y=aln(x)+b.

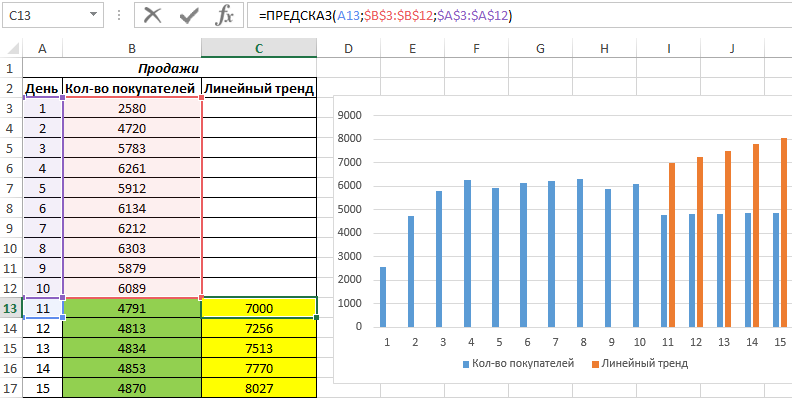
Для сопоставления, произведем расчет с внедрением функции линейного тренда:
И для зрительного сравнительного анализа построим обычный график.

Как видно, функцию линейной регрессии следует употреблять в тех вариантах, когда наблюдается неизменный рост какой-нибудь величины. В этом случае функция логарифмического тренда дозволяет получить наиболее правдоподобные данные (наиболее наглядно при большем количестве данных).
Прогнозирование будущих значений в Excel по условию
Пример 3. В таблице Excel указаны значения независящей и зависимой переменных. Некие значения зависимой переменной указаны в виде отрицательных чисел. Спрогнозировать несколько следующих значений зависимой переменной, исключив из расчетов отрицательные числа.
Вид таблицы данных:
Для расчета будущих значений Y без учета отрицательных значений (-5, -20 и -35) используем формулу:
C помощью функций ЕСЛИ производится перебор частей спектра B2:B11 и отброс отрицательных чисел. Так, получаем прогнозные данные на основании значений в строчках с номерами 2,3,5,6,8-10. Для детализированного анализа формулы изберите инструмент «ФОРМУЛЫ»-«Зависимости формул»-«Вычислить формулу». Один из шагов вычислений формулы:
Способы прогнозирования в Excel

Научитесь употреблять все прикладные инструменты из функционала MS Excel.
Хоть какому бизнесу любопытно заглянуть в будущее и верно ответить на вопросец: «А сколько средств мы заработаем за последующий период?» Ответить на такового рода вопросцы разрешают разные методики прогнозирования. В данной статье мы с вами разглядим несколько таковых методик и произведем все нужные расчеты в Excel. Еще более про анализ данных в Excel мы рассказываем на нашем открытом курсе «Аналитика в Excel».
Постановка задачки
Начальные данные
Для начала, давайте определимся, какие у нас есть начальные данные и что нам необходимо получить на выходе. Практически, все что у нас есть, это некие исторические данные. Если мы говорим о прогнозировании продаж, то историческими данными будут реализации за прошлые периоды.
Примечание. Собранные в различные моменты времени значения одной и той же величины образуют временной ряд. Каждое значение такового временного ряда именуется измерением. К примеру: данные о продажах за крайние 5 лет по месяцам — временной ряд; реализации за январь прошедшего года — измерение.
Составляющие прогноза
Последующий шаг: давайте определимся, что нам необходимо учитывать при построении прогноза. Когда мы исследуем наши данные, нам нужно учитывать последующие причины:
Эти три пт в совокупа образуют регулярную составляющую временного ряда.
Примечание. Не непременно все три элемента постоянной составляющей должны находиться в временном ряде.
Но, кроме постоянной составляющей, в временном ряде находится еще некое случайное отклонение. Интуитивно это понятно — реализации могут зависеть от почти всех причин, некие из которых могут быть случайными.
Вывод. Чтоб комплексно обрисовать временной ряд, нужно учитывать 2 основных компонента: регулярную составляющую (тренд + сезонность + цикличность) и случайную составляющую.
Виды моделей
Последующий вопросец, на который необходимо ответить при построении прогноза: “А какие модели временного ряда бывают?”
Обычно выделяют два главных вида:
Время от времени также выделают смешанную модель в отдельную группу:
С моделями мы обусловились, но сейчас возникает очередной вопросец: «А когда какую модель лучше употреблять?»
Традиционный вариант таковой:
— Аддитивная модель употребляется, если амплитуда колебаний более-менее неизменная;
— Мультипликативная – если амплитуда колебаний зависит от значения сезонной составляющие.
Решение задачки при помощи Excel
Итак, нужные теоретические познания мы с вами получили, настало время применить их на практике. Мы будем с вами употреблять традиционную аддитивную модель для построения прогноза. Но, мы построим с вами два прогноза:
Во всех руководствах, обычно, разбирается лишь линейный тренд, потому полиномиальная модель будет очень полезна вам и вашей работы!

Научитесь употреблять все прикладные инструменты из функционала MS Excel.
Модель с линейным трендом
Пусть у нас есть начальная информация по продажам за 2 года:

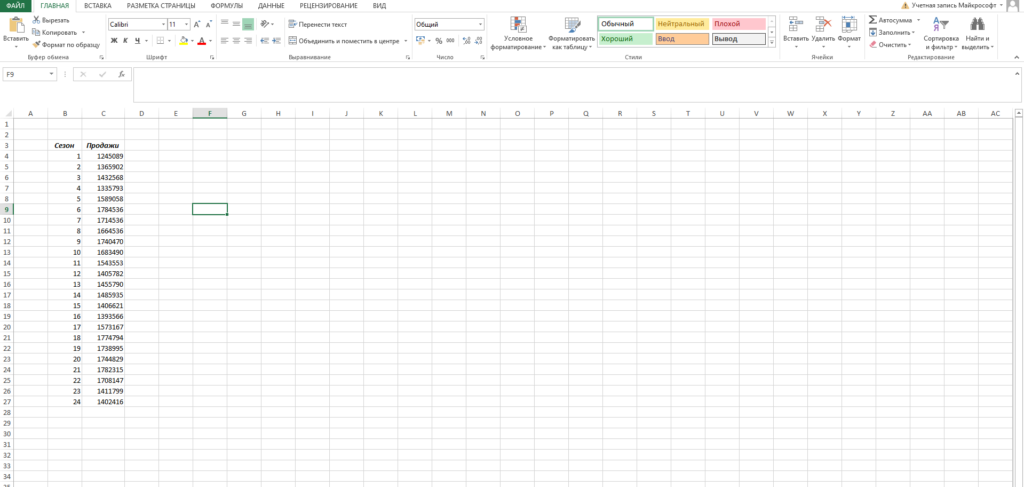
Беря во внимание, что мы используем линейный тренд, то нам нужно отыскать коэффициенты уравнения
Высчитать коэффициенты данного уравнения можно при помощи формулы массива и функции ЛИНЕЙН. Нам нужно будет создать последующую последовательность действий:
На выходе мы получили 2 числа: 1-ое — коэффициент a, 2-ое — вольный член b.

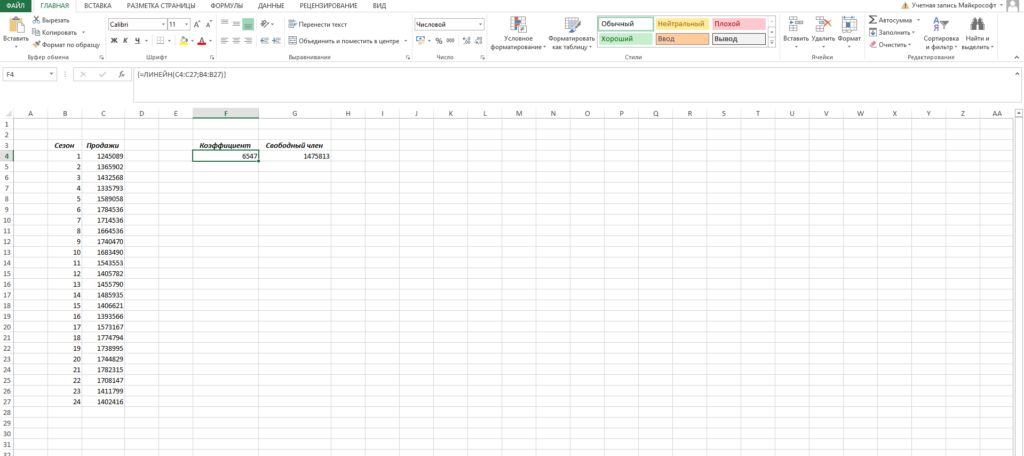
Сейчас нам необходимо высчитать для всякого периода значение линейного тренда. Создать это очень просто — довольно в приобретенное уравнение подставить известные номера периодов. К примеру, в нашем случае, мы прописываем формулу =B4*$F$4+$G$4 в ячейке I4 и протягиваем ее вниз по всем периодам.

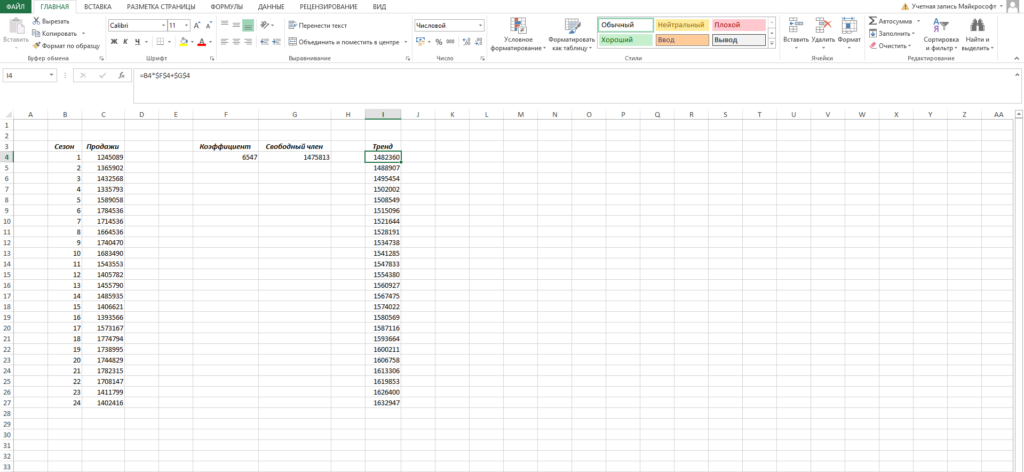
Нам осталось высчитать коэффициент сезонности для всякого периода. Беря во внимание, что у нас есть исторические данные за два года, уместно будет учитывать это при расчете. Можем создать последующим образом: в ячейке J4 прописываем формулу =(C4+C16)/СРЗНАЧ($C$4:$C$27)/2 и протягиваем вниз на 12 месяцев (т.е. до J15).

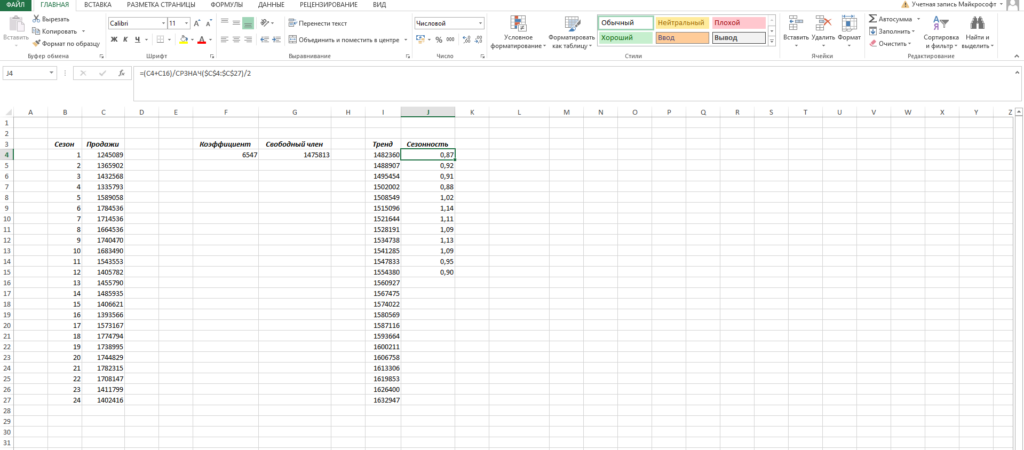
Что нам это отдало? Мы посчитали, сколько суммарно продавалось любой январь/любой февраль и так дальше, а позже разделили это на среднее значение продаж за все два периода.
Другими словами мы узнали, как реализации 2-ух январей отклонялись от средних продаж за два года, как реализации 2-ух февралей отклонялись и так дальше. Это и дает нам коэффициент сезонности. В конце формулы делим на 2, т.к. в расчете фигурировало 2 периода.
Примечание. Высчитали лишь 12 коэффициентов, т.к. один коэффициент учитывает реализации сходу за 2 подобных периода.
Итак, сейчас мы на финальной прямой. Нам осталось высчитать тренд для будущих периодов и учитывать коэффициент сезонности для их. Давайте амбициозно построим прогноз на год вперед.
Поначалу создаем столбец, в котором прописываем номера будущих периодов. В нашем случае нумерация начинается с 25 периода.
Дальше, для расчета значения тренда просто прописываем уже известную нам формулу =L4*$F$4+$G$4 и протягиваем вниз на все 12 предсказуемых периодов.
И крайний штришок — умножаем приобретенное значение на коэффициент сезонности. Вуаля, это и есть итоговый ответ в данной модели!

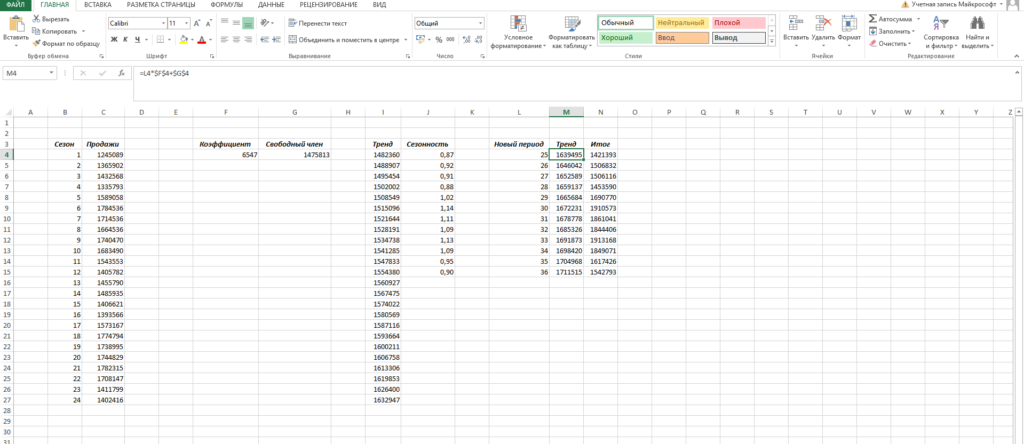
Модель с полиномиальным трендом
Система, которую мы лишь что с вами выстроили, довольно ординарна. Но у нее есть один большенный минус — далековато не постоянно она дает достоверные результаты.
Поглядите сами, какая модель наиболее буквально аппроксимирует наши точки — линейный тренд (ровная зеленоватая линия) либо полиномиальный тренд (красноватая кривая)? Ответ предельно ясен. Потому на данный момент мы с вами и разберем, как выстроить полиномиальную модель в Excel.

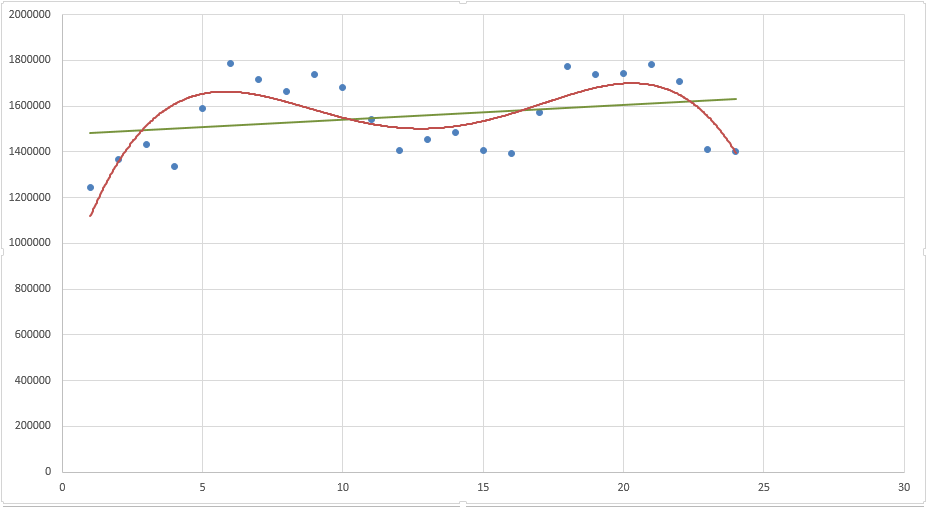
Пусть все начальные данные у нас будут таковыми же. Для простоты модели будем учесть лишь тренд, без сезонной составляющей.
Для начала давайте определимся, чем полиномиальный тренд различается от обыденного линейного. Верно — формой уравнения. У линейного тренда мы разбирали обыденный график прямой:

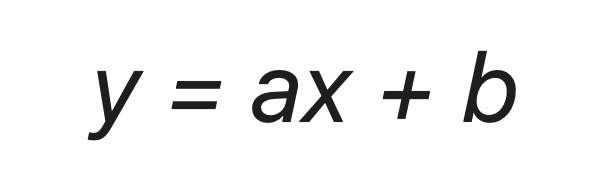
У полиномиального тренда же уравнение смотрится по другому:

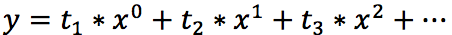
где конечная степень определяется степенью полинома.
Т.е. для полинома 4 степени нужно отыскать коэффициенты уравнения:

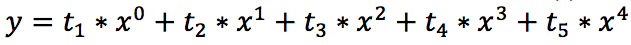
Согласитесь, смотрится мало жутко. Но, ничего ужасного нет, и мы с легкостью можем решить эту задачу при помощи уже узнаваемых нам способов.
К слову говоря, мы можем просто сами себя проверить. Давайте построим график наших продаж и добавим к нему полиномиальный тренд.
Сейчас вы наглядно сможете созидать, как рассчитанный тренд аппроксимирует начальные данные и как смотрится само уравнение. Можно сопоставить уравнение на графике с вашими коэффициентами. Сходится? Означает сделали все правильно!
Кроме всего остального, вы сможете сходу оценить точность аппроксимации (не вполне, но хотя бы первично). Это делается при помощи коэффициента R^2. Здесь у вас опять есть два пути:
Заключение
Мы с вами тщательно разобрали вопросец прогнозирования — исследовали нужные определения и виды моделей, выстроили аддитивную модель в Excel с внедрением линейного и полиномиального тренда, также научились показывать результаты собственных вычислений на графиках. Все это дозволит для вас отлично внедрять приобретенные познания на работе, усложнять имеющиеся модели и уточнять прогнозы. Чем огромным количеством способов и инструментов вы будете обладать, тем выше будет ваш проф уровень и статус на рынке труда.
Если вас заинтересовывают еще какие-то модели прогнозирования — напишите нам о этом, и мы попытаемся осветить эти темы в последующих собственных статьях! Либо запишитесь на курс «Excel Academy» от SF Education, где мы рассказываем про способности Excel, нужные для анализа.
Создатель: Алексанян Андрон, эксперт SF Education



Научитесь употреблять все прикладные инструменты из функционала MS Excel.