Диаграммы в Excel: Ряд данных

Строчки либо столбцы чисел, которые нанесены на график, именуются рядом данных. Вы сможете выстроить один либо несколько рядов данных на диаграмме.

Чтоб сделать гистограмму, сделайте последующие деяния:

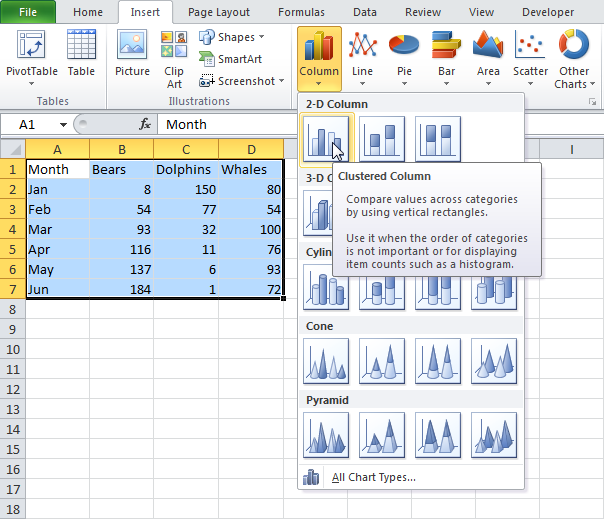
1. Выделите спектр A1:D7.
2. На вкладке Вставка (Insert) в разделе Диаграммы (Charts) кликните Вставить гистограмму > Гистограмма с группировкой (Column > Clustered Column).

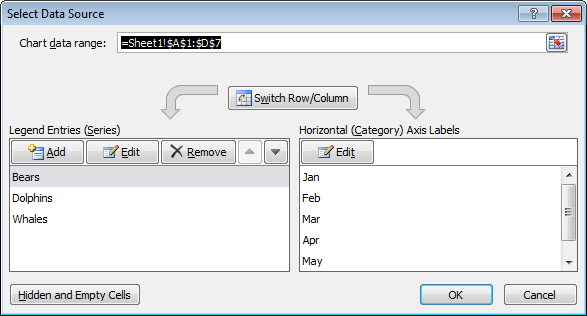
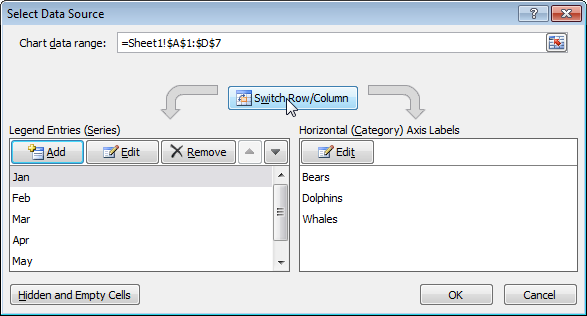
Выбор источника данных

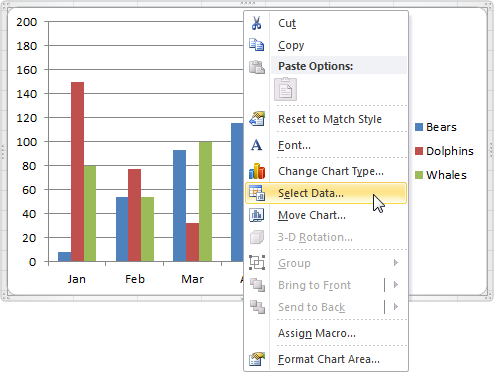
Чтоб открыть диалоговое окно Выбор источника данных (Select Data Source) сделайте последующие деяния:

1. Выделите диаграмму. Щелкните по ней правой клавишей мыши и нажмите Избрать данные (Select Data).Покажется диалоговое окно Выбор источника данных (Select Data Source).
2. Слева вы сможете узреть три ряда данных (Bears, Dolphins и Whales), а справа подписи горизонтальных осей (Jan, Feb, Mar, Apr, May и Jun).

Строчка/Столбец

Если вы кликните по кнопочке Строчка/Столбец (Switch Row/Column), то получите 6 рядов данных (Jan, Feb, Mar, Apr, May и Jun) и три подписи горизонтальных осей (Bears, Dolphins и Whales).

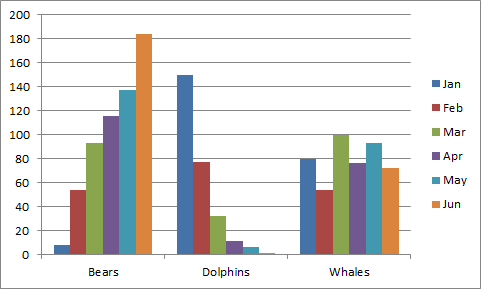
Добавление, изменение, удаление и перемещение

Вы сможете употреблять диалоговое окно Выбор источника данных (Select Data Source) для прибавления, редактирования, удаления и перемещения рядов данных, но есть наиболее резвый метод. Выделите диаграмму и просто измените спектр на листе.

Числовые последовательности в EXCEL (порядковые номера 1,2,3. и др.)

Сформируем последовательность 1, 2, 3, . Пусть в ячейке A2 введен 1-ый элемент последовательности — значение 1 . В ячейку А3 , вводим формулу =А2+1 и копируем ее в ячейки ниже (см. файл примера ).

Потому что в формуле мы сослались на ячейку выше при помощи относительной ссылки , то EXCEL при копировании вниз видоизменит вышеуказанную формулу в =А3+1 , потом в =А4+1 и т.д., тем формируя числовую последовательность 2, 3, 4, .

Если последовательность необходимо сформировать в строке, то формулу необходимо вводить в ячейку B2 и копировать ее необходимо не вниз, а на право.

Чтоб сформировать последовательность нечетных чисел вида 1, 3, 7, . нужно поменять формулу в ячейке А3 на =А2+2 . Чтоб сформировать последовательность 100, 200, 300, . нужно поменять формулу на =А2+100 , а в ячейку А2 ввести 100.

Остальным вариантом сотворения последовательности 1, 2, 3, . является внедрение формулы =СТРОКА()-СТРОКА($A$1) (если 1-ый элемент последовательности размещается в строке 2 ). Формула =СТРОКА(A2)-СТРОКА($A$1) дозволяет сделать вертикальную последовательность, в случае если ее 1-ый элемент последовательности размещается в хоть какой строке. Этот же итог дают формулы =ЧСТРОК($A$1:A1) , =СТРОКА(A1) и =СТРОКА(H1) . Формула =СТОЛБЕЦ(B1)-СТОЛБЕЦ($A$1) делает последовательность, размещенную горизонтально. Этот же итог дают формулы =ЧИСЛСТОЛБ($A$1:A1) , =СТОЛБЕЦ(A1) .

Чтоб сформировать последовательность I, II, III, IV , . начиная с ячейки А2 , введем в А2 формулу =РИМСКОЕ(СТРОКА()-СТРОКА($A$1))

Сформированная последовательность, строго говоря, не является числовой, т.к. функция РИМСКОЕ() возвращает текст. Таковым образом, сложить, к примеру, числа I+IV в прямую не получится.

Остальным видом числовой последовательности в текстовом формате является, к примеру, последовательность вида 00-01 , 00-02, . Чтоб начать нумерованный перечень с кода 00-01 , введите формулу =ТЕКСТ(СТРОКА(A1);»00-00″) в первую ячейку спектра и перетащите маркер наполнения в конец спектра.

Выше были приведены примеры арифметических последовательностей. Некие остальные виды последовательностей можно также сформировать формулами. К примеру, последовательность n2+1 ((n в степени 2) +1) сделаем формулой =(СТРОКА()-СТРОКА($A$1))^2+1 начиная с ячейки А2 .

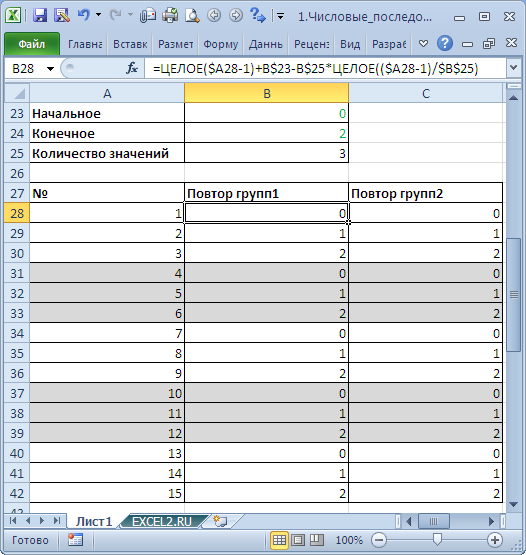
Сделаем последовательность с повторами вида 1, 1, 1, 2, 2, 2. Это можно создать формулой =ЦЕЛОЕ((ЧСТРОК(A$2:A2)-1)/3+1) . При помощи формулы =ЦЕЛОЕ((ЧСТРОК(A$2:A2)-1)/4+1)*2 получим последовательность 2, 2, 2, 2, 4, 4, 4, 4. , т.е. последовательность из четных чисел. Формула =ЦЕЛОЕ((ЧСТРОК(A$2:A2)-1)/4+1)*2-1 даст последовательность 1, 1, 1, 1, 3, 3, 3, 3, .

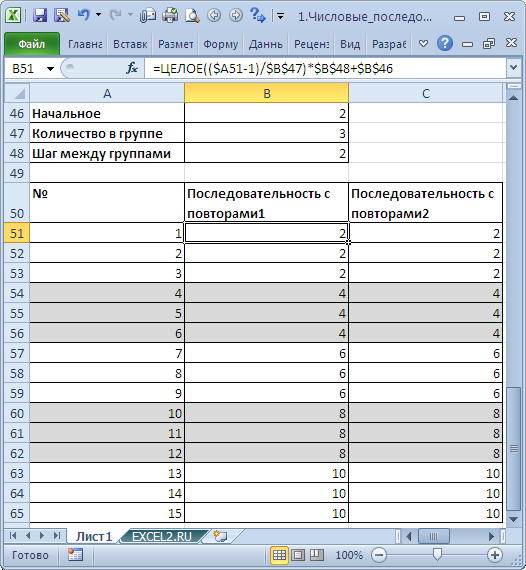
Примечание . Для выделения повторов применено Условное форматирование .

Формула =ОСТАТ(ЧСТРОК(A$2:A2)-1;4)+1 даст последовательность 1, 2, 3, 4, 1, 2, 3, 4, . Это пример последовательности с временами циклическими элементами.

Используем кнопку CTRL

Пусть, как и в прошлом примере, в ячейку A2 введено значение 1 . Выделим ячейку A2 . Удерживая кнопку CTRL , скопируем Маркером наполнения (при всем этом над курсором покажется небольшой плюсик), значение из A 2 в ячейки ниже. Получим последовательность чисел 1, 2, 3, 4 …

ВНИМАНИЕ! Если на листе часть строк укрыта при помощи фильтра , то этот подход и другие, приведенные ниже, работать не будут. Чтоб разрешить нумерацию строк с внедрением клавиши CTRL , выделите всякую ячейку с заголовком фильтра и два раза нажмите CTRL + SHIFT + L (сбросьте фильтр).

Используем правую кнопку мыши

Пусть в ячейку A2 введено значение 1 . Выделим ячейку A2 . Удерживая правую кнопку мыши, скопируем Маркером наполнения , значение из A2 в ячейки ниже. Опосля того, как отпустим правую кнопку мыши покажется контекстное меню, в котором необходимо избрать пункт Заполнить . Получим последовательность чисел 1, 2, 3, 4 …

Используем начало последовательности

Если начало последовательности уже задано (т.е. задан 1-ый элемент и шаг последовательности), то сделать последовательность 1, 2, 3, . можно последующим образом:

• пусть в ячейке А2 введено значение 1 , а в ячейке А3 значение 2 ;
• выделяем ячейки A2 и A3 ;
• беремся за правый нижний угол и Маркером наполнения протягиваем вниз.

Получаем итог как в прошлом случае. Если в ячейке А3 введено значение 3 , т.е. задан шаг последовательности равный 2, то мы получим последовательность нечетных чисел.

Сделаем последовательность вида 1, 2, 3, 1, 2, 3. для этого введем в 1-ые три ячейки значения 1, 2, 3, потом маркером наполнения , удерживая кнопку CTRL , скопируем значения вниз.

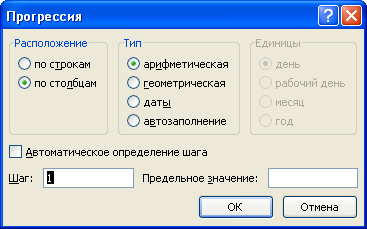
Внедрение инструмента Прогрессия

Воспользуемся обычным средством EXCEL для сотворения прогрессий, в то числе и арифметических.

• вводим в ячейку А2 значение 1 ;
• выделяем спектр A2:А6 , в котором будут содержаться элементы последовательности;
• вызываем инструмент Прогрессия ( Основная/ Редактирование/ Заполнить/ Прогрессия. ), в показавшемся окне жмем ОК.

Внедрение в работе : Подходы для сотворения числовых последовательностей можно употреблять для нумерации строк , сортировки перечня с числами , разнесения значений по столбцам и строчкам .

СОВЕТ: О текстовых последовательностях вида 1-ый, 2-ой, . 1), 2), 3), . можно прочесть в статье Текстовые последовательности . О последовательностях значений в формате дат (и времени) вида 01.01.09, 01.02.09, 01.03.09, . янв, апр, июл, . пн, вт, ср, . можно прочесть в статье Последовательности дат и времен . О массивах значений, содержащих последовательности конечной длины, применяемых в формулах массива , читайте в статье Массив значений (либо константа массива либо массив констант) .

Подсчет неповторимых значений в Excel

В этом руководстве вы узнаете, как посчитать неповторимые значения в Excel при помощи формул и как это создать в сводной таблице. Мы также разберём несколько примеров счёта неповторимых текстовых и числовых значений, в том числе с учетом регистра букв.

При работе с огромным набором данных в Excel для вас нередко может потребоваться знать, сколько в вашей таблице циклических и сколько неповторимых записей.

И вот о чем мы на данный момент побеседуем:

Если вы часто посещаете этот блог, вы уже понимаете формулу Excel для подсчета дубликатов. А сейчас мы собираемся изучить разные методы подсчета неповторимых значений в Excel. Но для ясности давайте поначалу определимся с определениями.

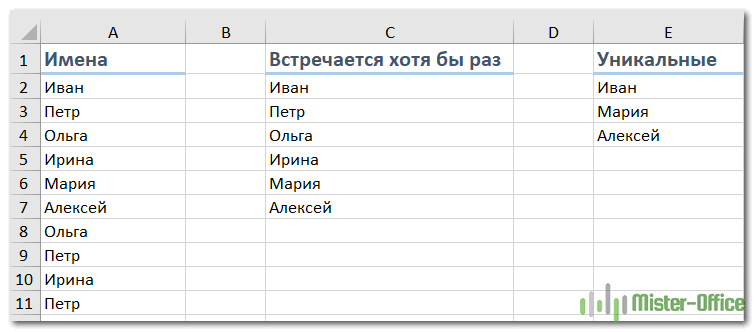
• Неповторимые значения – те, которые возникают в перечне лишь один раз.
• Разные – это все, которые имеются в перечне без учета повторов, другими словами неповторимые плюс 1-ое вхождение циклических.

Последующий набросок иллюстрирует эту разницу:

А сейчас давайте поглядим, как можно их посчитать при помощи формул и функций сводной таблицы.

Дальше вы отыщите несколько примеров для подсчета неповторимых данных различных типов.

Считаем неповторимые значения в столбце.

Представим, у вас есть столбец с именами на листе Excel, и для вас необходимо подсчитать, сколько там есть неповторяющихся. Самое обычное решение состоит в том, чтоб употреблять функцию СУММ в сочетании с ЕСЛИ и СЧЁТЕСЛИ :

Примечание. Это формула массива, потому непременно нажмите Ctrl + Shift + Enter, чтоб корректно ввести её. Как вы это сделаете, Excel автоматом заключит всё выражение в <фигурные скобки>, как показано на снимке экрана ниже. Ни в коем случае недозволено вводить фигурные скобки вручную, это не сработает.

В этом примере мы считаем неповторимые имена в спектре A2: A10, потому наше выражение смотрится так:

Этот способ подступает и для текстовых, и для цифровых данных. Недочетом будет то, что в качестве неповторимого он будет пересчитывать хоть какое содержимое, в том числе и ошибки.

Дальше в этом руководстве мы обсудим несколько остальных подходов для подсчета неповторимых значений различных типов. И так как в основном они являются вариантами данной базисной формулы, имеет смысл тщательно разглядеть её. Если вы поймете, как это работает, то можете настроить ее для собственных данных. Если кого-либо не заинтересовывают технические подробности, вы сможете сходу перейти к последующему примеру.

Как работает формула подсчета неповторимых значений?

Видите ли, тут употребляются 3 различные функции – СУММ, ЕСЛИ и СЧЁТЕСЛИ. Поглядим, что делает любая из их:

• Функция СЧЁТЕСЛИ считает, сколько раз каждое отдельное значение возникает в анализируемом спектре.

В этом примере СЧЁТЕСЛИ(A2:A10;A2:A10)возвращает массив <3:2:2:1:1:2:3:2:3>.

• Функция ЕСЛИ оценивает любой элемент в этом массиве, сохраняет все единицы (другими словами, неповторимые) и подменяет все другие числа нулями.

Итак, функция ЕСЛИ(СЧЁТЕСЛИ(A2:A10;A2:A10)=1;1;0) преобразуется в ЕСЛИ(<3:2:2:1:1:2:3:2:3>) = 1,1,0).

И дальше она преобразуется в массив чисел <0:0:0:1:1:0:0:0:0>. Тут 1 значит неповторимое значение, а 0 – появляющееся наиболее 1 раза.

• В конце концов, функция СУММ складывает числа в этом итоговом массиве и выводит полное количество неповторимых значений. Что нам и необходимо.

Совет. Чтоб выяснить, какой итог дает какая-то определенная часть выражения, выделите эту часть в строке формул и нажмите многофункциональную кнопку F9.

Подсчет неповторимых текстовых значений.

Если ваш перечень содержит как числа так и текст, и вы желаете посчитать лишь неповторимые текстовые строчки, добавьте функцию ЕТЕКСТ() в формулу массива, описанную выше:

Функция ЕТЕКСТ возвращает ИСТИНА, если исследуемое содержимое ячейки является текстом, и ЛОЖЬ в обратном случае. Так как звездочка (*) в формулах массива работает как оператор И, то функция ЕСЛИ возвращает 1, лишь если рассматриваемое сразу текстовое и неповторимое, в неприятном случае получаем 0. И опосля того, как функция СУММ сложит все числа, вы получите количество неповторимых текстовых значений в обозначенном спектре.

Не запамятовывайте жать Ctrl + Shift + Enter , чтоб верно ввести формулу массива, и вы получите итог, схожий этому:

Как вы сможете созидать на снимке экрана выше, мы получили полное количество неповторимых текстовых значений, исключая пустые ячейки, числа, логические выражения ИСТИНА и ЛОЖЬ, также ошибки.

Как сосчитать неповторимые числовые значения.

Чтоб посчитать неповторимые числа в перечне данных, используйте формулу массива буквально так же, как мы лишь что делали при подсчете текстовых данных. Отличие заключается в том, что вы используете ЕЧИСЛО заместо ЕТЕКСТ:

Пример и итог вы видите на снимке экрана чуток выше.

Примечание. Так как Microsoft Excel хранит дату и время как числа, они также участвуют в подсчёте.

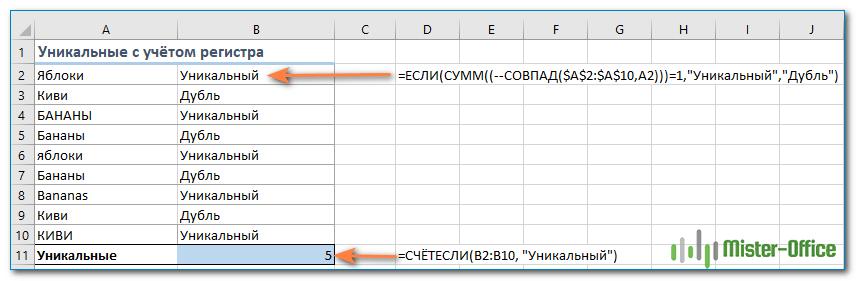
Неповторимые значения с учетом регистра.

Если вам принципно различие в больших и строчных буковках, то самым обычным методом подсчета будет создание вспомогательного столбца со последующей формулой массива для идентификации циклических и неповторимых частей:

А потом используйте ординарную функцию СЧЁТЕСЛИ для подсчета неповторимых значений:

А сейчас поглядим, как можно посчитать количество значений, которые возникают хотя бы один раз, другими словами так именуемых разных значений.

Подсчет разных значений.

Используйте последующую всепригодное выражение:

Помните, что это формула массива, потому для вас следует надавить Ctrl + Shift + Enter , заместо обыденного Enter.

Не считая того, вы сможете употреблять функцию СУММПРОИЗВ и записать формулу обыденным методом:

=СУММПРОИЗВ(1 / СЧЁТЕСЛИ( спектр ; спектр ))

К примеру, чтоб сосчитать разные значения в спектре A2: A10, вы сможете употреблять выражение:

Этот метод подступает не только лишь для подсчета в столбце, да и для спектра данных. Например, у нас под имена отведено две колонки. Тогда делаем так:

Этот способ подступает для текста, чисел, дат.

Единственное ограничение – спектр должен быть непрерывным и не содержать пустых ячеек и ошибок.

Если в вашем спектре данных есть пустые ячейки, то можно поменять:

Тогда в расчёт попадёт и будет засчитана и пустая ячейка.

Как это работает?

Как вы уже понимаете, мы используем функцию СЧЁТЕСЛИ, чтоб выяснить, сколько раз любой отдельный элемент встречается в обозначенном спектре. В приведенном выше примере, итог работы функции СЧЕТЕСЛИ представляет собой числовой массив: <3:2:2:1:3:2:1:2:3>.

Опосля этого производится ряд операций деления, где единица делится на каждую цифру из этого массива. Это превращает все неуникальные значения в дробные числа, надлежащие количеству повторов. К примеру, если число либо текст возникает в перечне 2 раза, в массиве создаются 2 элемента равные 0,5 (1/2 = 0,5). А если возникает 3 раза, в массиве создаются 3 элемента 0,333333.

В нашем примере результатом вычисления выражения 1/СЧЁТЕСЛИ(A2:A10;A2:A10) является массив <0.333333333333333:0.5:0.5:1:0.333333333333333:0.5:1:0.5:0.333333333333333>.

Пока не очень понятно? Это поэтому, что мы еще не применили функцию СУММ / СУММПРОИЗВ. Когда одна из этих функций складывает числа в массиве, сумма всех дробных чисел для всякого отдельного элемента постоянно дает 1, независимо от того, сколько раз он возникал. И так как все неповторимые элементы показываются в массиве как единицы (1/1 = 1), окончательный итог представляет собой полное количество всех встречающихся значений.

Как и в случае подсчета неповторимых значений в Excel, вы сможете употреблять варианты всепригодной формулы для обработки раздельно чисел, текста либо же с учетом регистра.

Помните, что все приведенные ниже выражения являются формулами массива и требуют нажатия Ctrl + Shift + Enter .

Подсчет разных значений без учета пустых ячеек

Если столбец, в котором вы желаете совершить подсчет, может содержать пустые ячейки, для вас следует в уже знакомую нам формулу массива добавить функцию ЕСЛИ. Она будет инспектировать ячейки на наличие пустот (основная формула Excel, описанная выше, в этом случае возвратит ошибку #ДЕЛ/0):

Ах так, например, можно посчитать количество личных значений, игнорируя пустые ячейки:

Видите ли, наш перечень состоит из трёх имён.

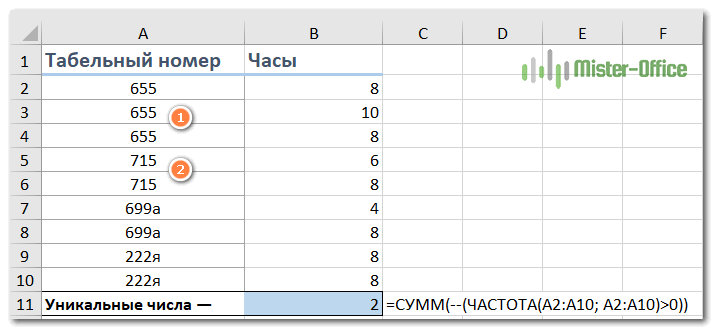
Подсчет разных чисел.

Чтоб посчитать разные числовые значения (числа, даты и время), используйте функцию ЕЧИСЛО:

Считаем, сколько имеется разных чисел в спектре A2: A10:

Итог вы сможете поглядеть ниже.

Это довольно обычное и стильное решение, но работает оно еще медлительнее, чем выражения, которые употребляют функцию ЧАСТОТА для подсчета неповторимых значений. Если у вас огромные наборы данных, то целенаправлено переключиться на формулу, основанную на расчёте частот.

И вот очередной метод подсчета чисел:

Применительно например ниже:

Видите ли, тут игнорируются записи, в которых имеются буковкы.

Пошагово разберём, как это работает.

Функция ЧАСТОТА возвращает массив цифр, которые соответствуют интервалам, данным имеющимися числами. В этом случае мы сравниваем один и этот же набор чисел для массива данных и для массива интервалов.

Результатом будет то, что ЧАСТОТА() возвращает массив, который представляет собой счетчик для всякого числового значения в массиве данных.

Это работает, поэтому что ЧАСТОТА() возвращает ноль для всех чисел, которые ранее уже возникли в перечне. Ноль ворачивается и для текстовых данных. Потому приобретенный массив смотрится последующим образом:

Видите ли, обрабатываются лишь числа. Ячейки A7:A10 игнорируются, поэтому что там текст. А функция ЧАСТОТА() работает лишь с числами.

Сейчас каждое из этих чисел проверяем на условие «больше нуля».

Сейчас превращаем ИСТИНА и ЛОЖЬ в 1 и 0 соответственно. Делаем это с помощью двойного отрицания. Проще говоря, это двойной минус, который не меняет величину числа, но дозволяет получить настоящие числа, когда это совершенно может быть: