Построение диаграмм с несколькими рядами данных в EXCEL

Построение диаграмм с одним рядом данных рассмотрено в статье Базы построения диаграмм в MS EXCEL . Начинающим юзерам также целенаправлено перед чтением ознакомиться со статьей Главные типы диаграмм .

ГИСТОГРАММА

Построим Гистограмму с группировкой на базе таблицы с 2-мя числовыми столбцами, близких по значениям.

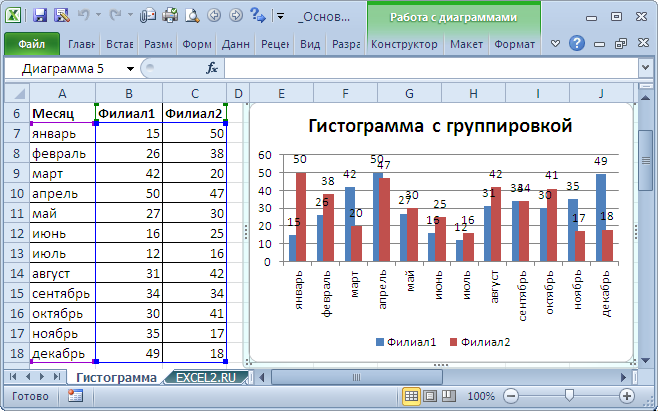
Выделите всякую ячейку таблицы (см. файл примера ), на вкладке Вставка , в группе Диаграммы нажмите клавишу Гистограмма , в выпавшем меню изберите Гистограмма с группировкой .

MS EXCEL выстроит оба ряда с внедрением лишь главных осей (чтоб в этом убедиться, два раза кликните поначалу по столбцу 1-го ряда, потом по одному из столбцов по другого. В окне Формат ряда данных на вкладке Характеристики ряда будет обозначено по какой оси отложены значения ряда). Т.к. значения у обоих рядов близки, то такое решение нам подступает.

Для рядов, у каких значения значительно различаются (на порядок и больше) один из рядов необходимо строить с внедрением Вспомогательной вертикальной оси .

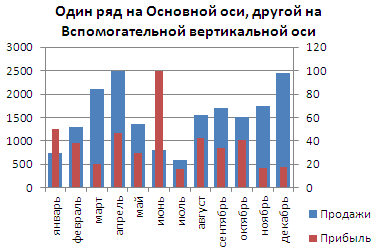
Для этого довольно избрать для 1-го из рядов построение на вспомогательной оси (два раза кликнув на один из столбцов), а потом настроить ширину столбцов (боковой зазор), чтоб показывались оба ряда.

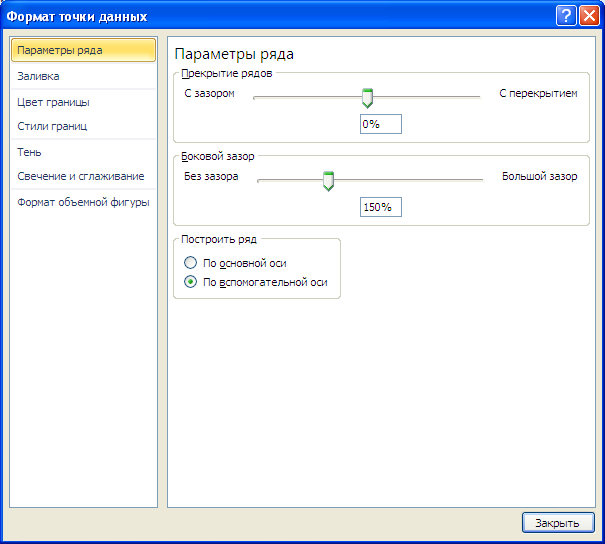
Если не настроить ширину столбцов, то эту диаграмму можно спутать с диаграммой Гистограмма с пополнением (столбцы, относящие к одной группы «ставятся» друг на друга).

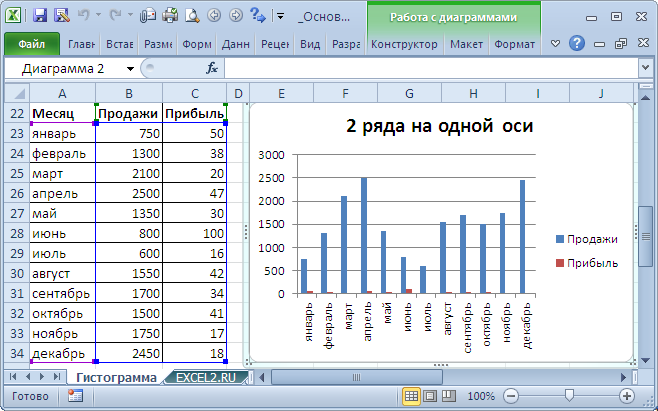
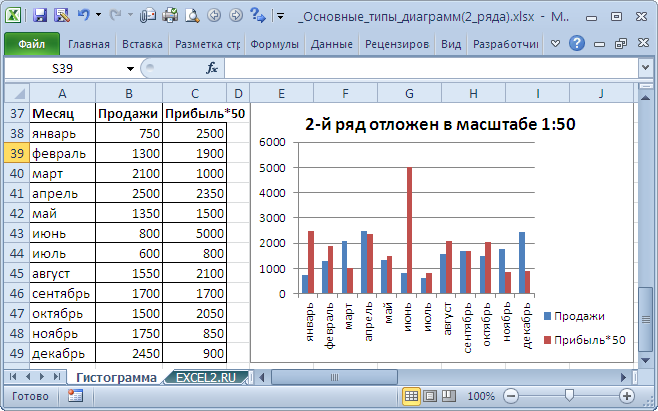
Иной возможностью отображения на диаграмме 2-ух рядов со существенно различающимися значениями, является масштабирование самих значений в таблице-источнике.

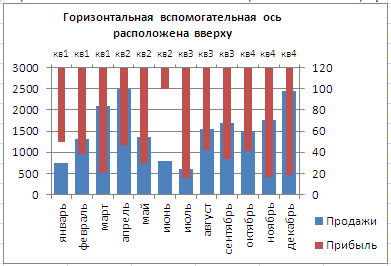
Горизонтальную вспомогательную ось можно расположить даже вверху. При всем этом столбцы различных рядов будут оригинально пересекаться.

Сейчас изменим подписи по горизонтальной оси (группы).

В окне Выбор источника данных видно, что для обоих рядов подписи горизонтальной оси схожи, т.к. группы схожи для обоих рядов (столбец Месяц).

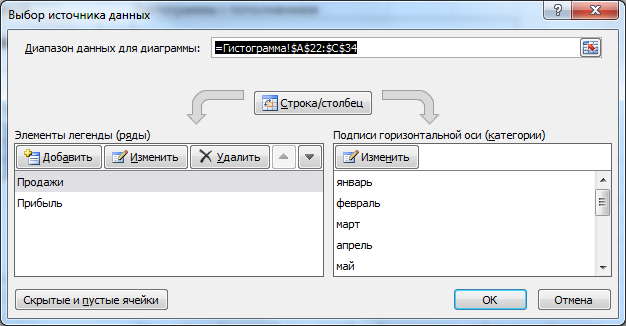
Кликните поначалу по ряду Реализации, потом по Прибыль — подписи по горизонтальной оси будут схожи.

При желании это также можно поменять. В окне Выбор источника данных выделите ряд Прибыль, нажмите клавишу Поменять расположенную справа, удалите ссылку на ячейки. Сейчас у ряда Прибыль заместо наименования категорий будут просто порядковые числа 1, 2, 3,… Но, они не будут отображаться на диаграмме, т.к. отображается пока лишь Основная горизонтальная ось .

Сейчас в меню Оси (вкладка Макет , группа Оси ) изберите Вспомогательная горизонтальная ось и установите ее Слева вправо . В окне формата Вспомогательной вертикальной оси измените точку пересечения оси (установите Автовыбор ). Получим вот такую диаграмму.

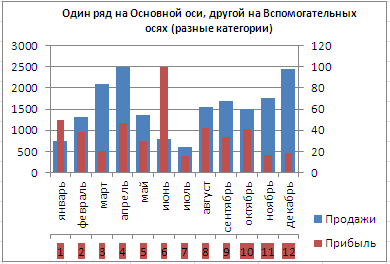
Хотя техно возможность отображения 2-х разных категорий существует, естественно, таковых диаграмм необходимо избегать, т.к. их трудно принимать. Группы должны быть схожими для всех рядов на диаграмме. Естественно, таковой трюк сработает лишь для 2-ух групп рядов, т.к. имеется всего 2 типа оси: основная и вспомогательная.

ГРАФИК

Диаграмма График почти во всем подобна Гистограмме с группировкой: к ней применимы те же идеи по отображению 2-ух рядов со существенно отличающимися значениями, что и к Гистограмме.

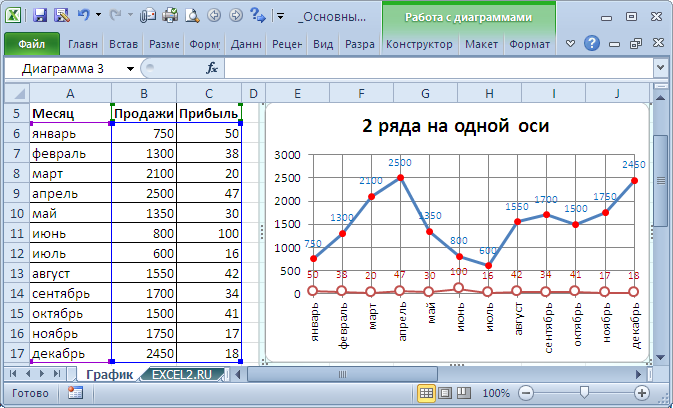
Опосля размещения рядов на различных осях получим вот такую диаграмму (полосы вертикальных осей выделены цветами, надлежащими цветам рядов).

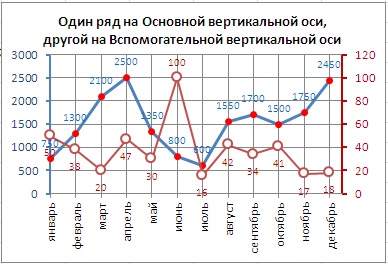
Примечание . Если провести горизонтальные полосы сетки к вспомогательной оси, то они, естественно, могут не совпасть с линиями к главный оси, т.к. масштабы осей (величины главных делений вертикальных осей) могут не совпадать. Это может «перегрузить» диаграмму.

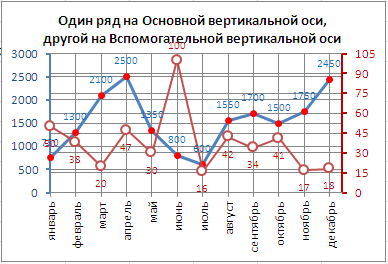
Совершенно, к использованию вспомогательных вертикальных осей, а тем наиболее вспомогательных горизонтальных осей для Гистограммы и Графика необходимо подступать продуманно: ведь диаграмма обязана «читаться» — быть понятной без доп объяснений.

ТОЧЕЧНАЯ

Зрительно Точечная диаграмма похожа на диаграмму типа График (если естественно у Точечной диаграммы точки соединены линиями).

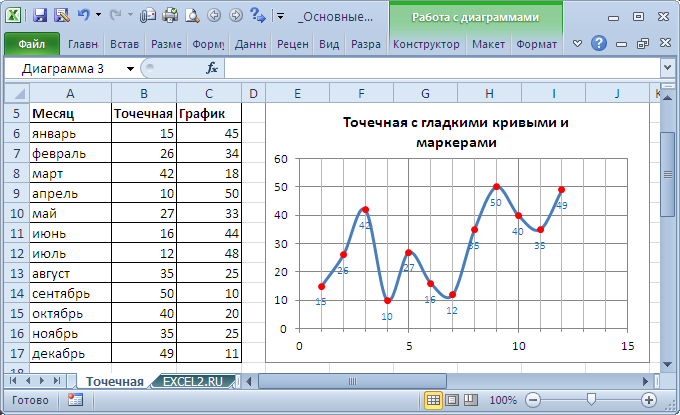
Различие состоит в том, что для построения Графика в качестве координаты Х постоянно употребляется последовательность 1, 2, 3, … (с подписями — категориями), а для Точечной значения по горизонтальной оси м.б. хоть какими числами (см. статью График vs Точечная ).

Примечание . Если для построения Точечной диаграммы не указана ссылка на значения Х (либо ссылка показывает на текстовые значения), то в качестве координат по Х будет применена та же последовательность 1, 2, 3, …, что и для Графика.

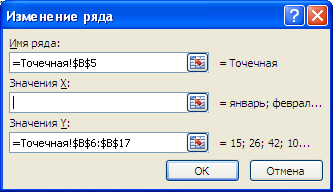
Исходя из вышесказанного, при построении диаграммы Точечная целенаправлено указывать числовые значения по Х. В неприятном случае необходимо просто употреблять График, т.к. для него можно задавать любые подписи по Х (в том числе и текстовые), что для Точечной диаграммы создать недозволено (лишь числа).

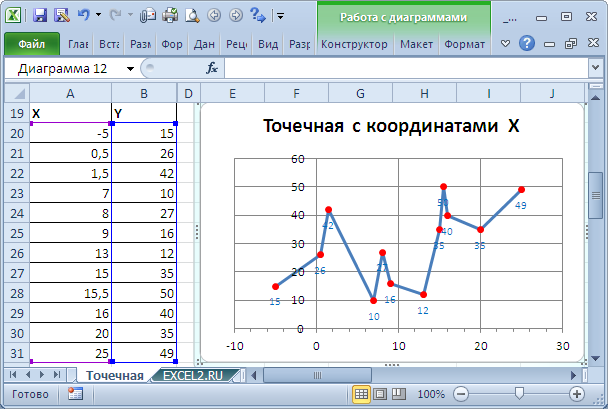
Сейчас о совмещении различных типов диаграмм с Точечной. Если для Точечной диаграммы не употребляется координата Х, то на диаграмме она смотрится как График.

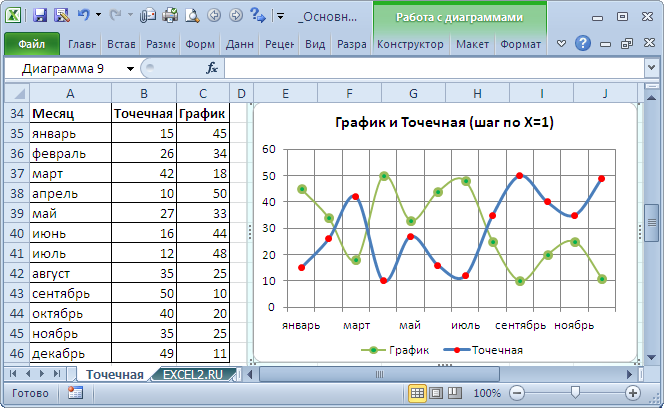
Подписи по горизонтальной оси берутся от Графика. В окне Выбор источника данных видно, что для ряда отображаемого Точечной диаграммой подписи горизонтальной оси схожи поменять/ удалить недозволено.

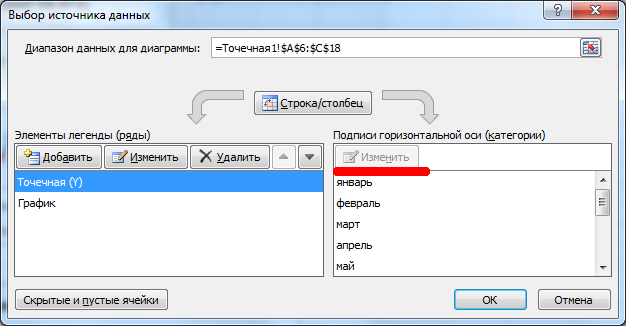
Не считая того, График быть может лишь на главный оси и поменять это недозволено.

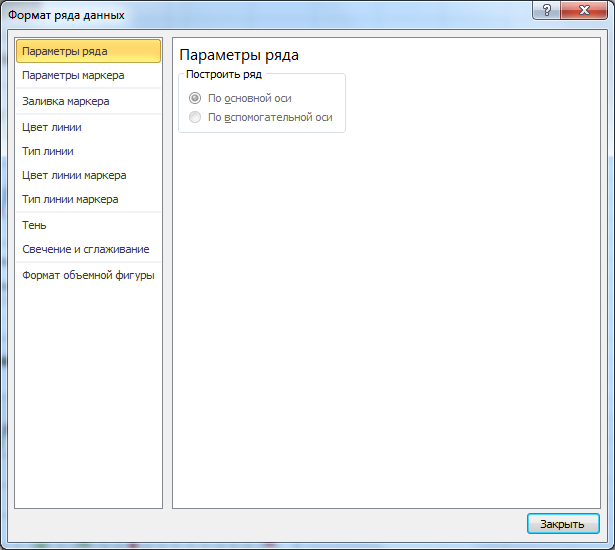
Если для Точечной диаграммы употребляется координата Х и оба ряда отложены по одной (главный) оси, то выходит не весьма прекрасная диаграмма.

Это соединено с тем, что при совмещении с Точечной диаграммой (на одной оси и когда у Точечной указаны значения по Х), диаграмма типа График становится вроде бы главной:

• на горизонтальной оси показываются подписи лишь для Графика;
• вертикальная сетка не отображается для отрицательных значений Х (т.к. График строится лишь для Х=1, 2, 3, …);
• у Графика нереально поменять Ось с Главный на Вспомогательную (у Точечной можно).

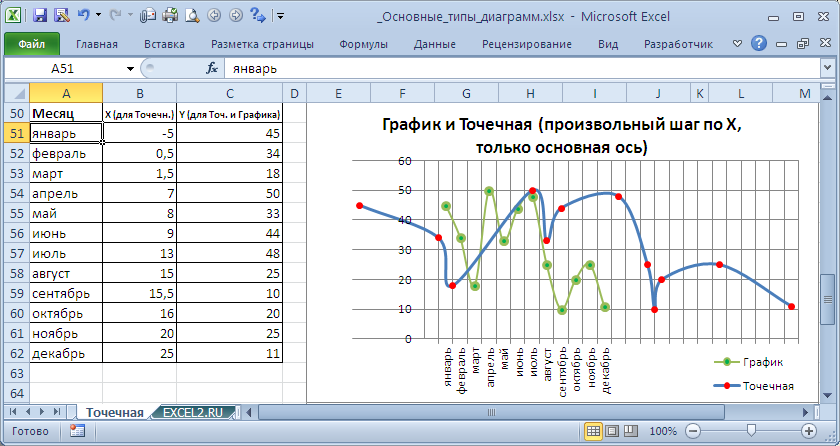
Если Точечную выстроить на вспомогательной оси, то диаграмма поменяется.

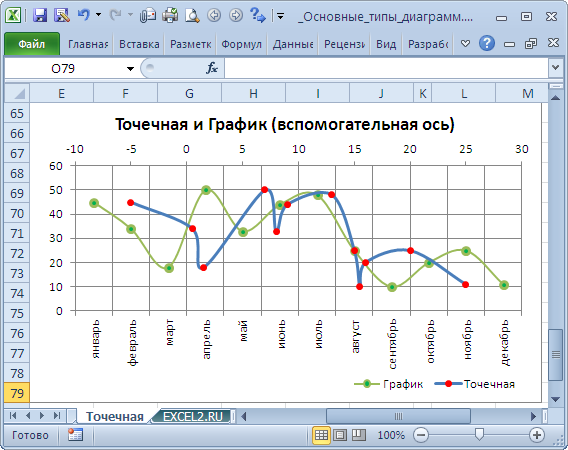
Подписи для Точечной (значения по Х) сейчас показываются сверху.

Совет . Диаграмма типа Точечная употребляется для построения окружностей, эллипсов и остальных замкнутых фигур на плоскости .

Сейчас разглядим построение 2-х рядов данных, которые употребляют диаграмму Точечная.

Поначалу построим 2 эллипса с разными координатами центра и размерами полуосей без использования вспомогательных осей.

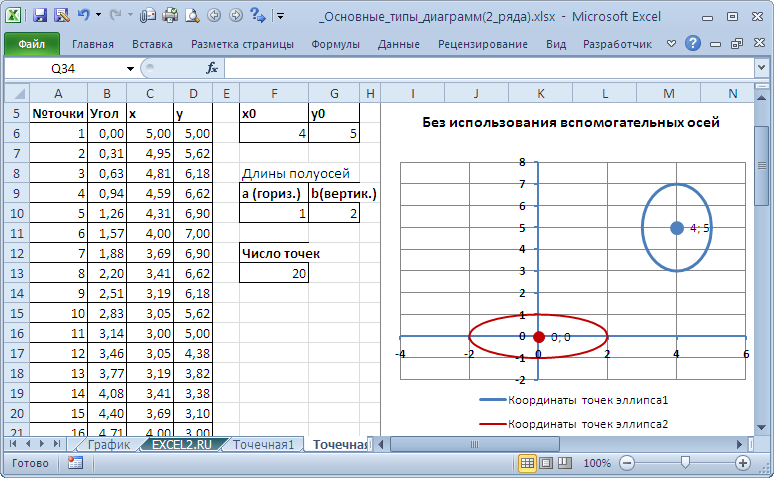
Примечание . Практически на диаграмме 4 ряда данных: точка центра представляет отдельный ряд.

Два раза кликнем по бордовому эллипсу и выберем построение ряда на вспомогательной оси (создадим то же и центра эллипса).

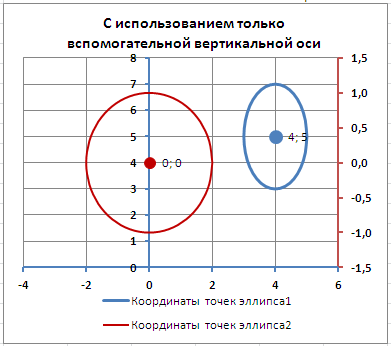
Сейчас координаты Y для красного эллипса откладываются по правой вертикальной оси (можно ее для наглядности выделить также бордовым цветом).

Добавим Вспомогательную горизонтальную ось (в меню Оси (вкладка Макет , группа Оси ) изберите Вспомогательная горизонтальная ось и установите ее По дефлоту ).

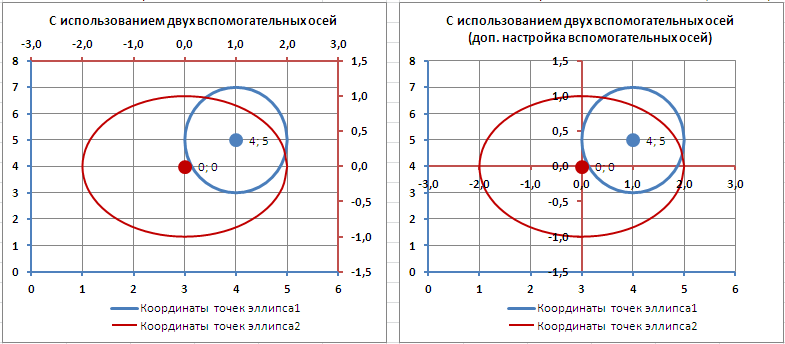
Наверняка, для диаграммы типа Точечная внедрение вспомогательных осей более оправдано – это дозволяет показывать на одной диаграмме разные по масштабу кривые.

КРУГОВАЯ

В статье Главные типы диаграмм показано, что расположить несколько рядов в радиальный диаграмме на техническом уровне можно, но, обычно, не целенаправлено.

Совмещение различных типов диаграмм

Про совмещение Графика и Точечной диаграммы поведано выше (см. раздел Точечная).

Совмещением Линейчатой и Гистограммы не стоит заниматься, т.к. смотрится это довольно удивительно, практически также удивительно, как и совмещение Гистограммы с Радиальный (см. также статью Главные типы диаграмм, раздел Радиальная ).

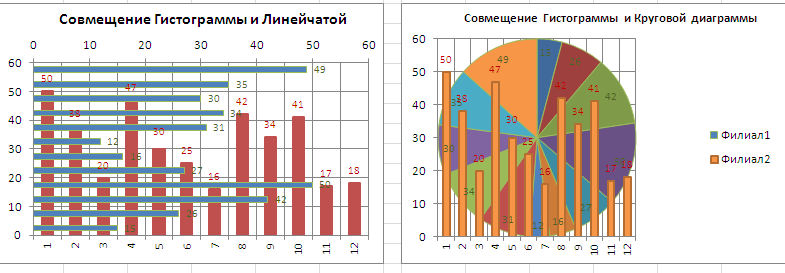
Совет . Также можно поглядеть статью Совмещаем различные типы диаграмм .

Оригинальностью совмещения могут также повытрепываться Гистограмма и Нормированная линейчатая с скоплением .

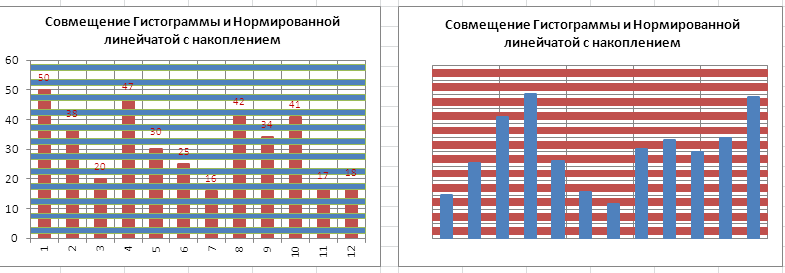
Наверняка, единственными типами диаграмм, которые стоит кооперировать, являются График и Гистограмма (группы должны быть схожими для обоих рядов).

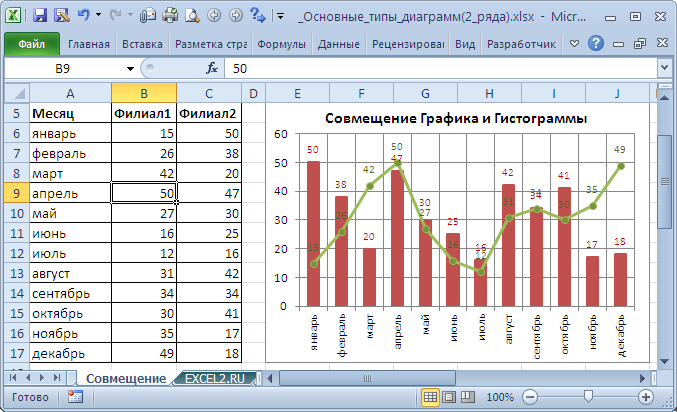
Для таковой диаграммы постройте поначалу Гистограмму с группировкой с 2-мя рядами (см. раздел Гистограмма в начале данной статьи). Потом выделите подходящий ряд и нажмите клавишу Поменять тип диаграммы (вкладка Конструктор ). Выбрав График либо График с Маркерами нажмите ОК.

Если масштабы значений у рядов значительно различаются, то можно настроить вспомогательную вертикальную ось (см. раздел Гистограмма).

Как создать точечный график в excel?

При помощи точечной диаграммы в Excel можно изобразить данные, расположенные в столбцах и строчках. График этого типа указывает дела меж числами в нескольких рядах данных либо две группы значений как один ряд координат х и у.

Где употребляется точечная диаграмма

В точечной диаграмме одни значения выводятся вдоль горизонтальной оси Х, остальные – вертикальной оси У. Эти числовые значения соединяются воединыжды в точку. А точки выводятся через неравные промежутки либо кластеры.

При помощи точечных диаграмм отлично ассоциировать и показывать научную, статистическую либо техно информацию. Подобные графики рекомендуются при последующих критериях:

• необходимо поменять масштаб оси Х;
• для горизонтальной оси употребляется логарифмическая шкала;
• числовые значения размещены неравномерно;
• горизонтальная ось представлена обилием точек;
• нужно показать данные таблицы, содержащие пары сгруппированных значений, и вывести самостоятельные шкалы точечного графика для иллюстрации доборной инфы о сгруппированных данных;
• требуется показать аналогию меж точками в огромных наборах данных.

При помощи точечной диаграммы можно ассоциировать сходу много точек без учета времени. Сопоставление будет тем поточнее, чем больше значений будет применено.

Как выстроить точечную диаграмму в Excel

Возьмем примерный набор данных, которые необходимо нанести на точечную диаграмму:

1. Выделяем значения, которые необходимо иллюстрировать при помощи точечной диаграммы. Перебегаем на вкладку «Вставка». В группе «Диаграммы» находим тип «Точечная».
2. Из предлагаемых вариантов выберем «Точечную с маркерами». Она подойдет для сопоставления пар значений.
3. Получаем диаграмму такового вида:
4. Активизируем инструмент «Работа с диаграммами». Для этого необходимо щелкнуть мышкой по области диаграммы. Поменяем стиль – создадим точки красноватыми. Добавим заглавие (на вкладке «Макет») – «Количество заключенных менеджерами договоров». Чтоб поменять размер шрифта, выделим заглавие и щелкнем правой клавишей мыши. В контекстном меню выберем поле «Шрифт».
5. Зададим наименования осей. В одноименной группе на вкладке «Макет» избираем заглавие для горизонтальной оси («под осью»), вводим подходящий текст. Для вертикальной оси – «Повернутое заглавие».
6. Вводим заглавие для оси и нажимаем ВВОД.

Точечная диаграмма различается от остальных типов методом отображения характеристик по горизонтальной оси. Средняя длительность разговора с клиентом из первого столбца показана в виде значений Х. Количество договоров из второго столбца – в виде значений Y. Другими словами один набор числовых данных постоянно формируется вдоль горизонтальной оси значений. А 2-ой набор – вдоль вертикальной оси, тоже значений.

На пересечении координат – точка данных, которая соединяет воединыжды два числовых значения. В нашем примере 1-ая точка данных на рисунке представлена значением Y (16, ячейка В8) и значением Х (2, А8). Вышла точечная диаграмма связи характеристик.

Подтипы точечной диаграммы

1. Мы выстроили точечную диаграмму с маркерами, которая дозволяет ассоциировать пары значений. Таковой подтип рекомендуется использовать, когда много данных (соединительная линия лишь сделает труднее восприятие) либо нет нужды демонстрировать связь меж точками.
2. На точечной диаграмме со значениями, соединенными сглаживающими линиями, точки данных объединены гладкой кривой. Можно созодать с маркерами либо без. Без маркеров – когда много начальных данных.
3. В диаграмме с прямыми отрезками меж точками – прямые соединительные полосы. Юзер может задать с маркерами либо без.

Таковым образом, числовые значения показываются на точечной диаграмме в виде единых точек данных. Интервалы могут быть равномерными и неравномерными. Горизонтальная ось – постоянно ось значений. Набор характеристик для ее шкалы не ограничен (по сопоставлению с осью категорий).

Точечную диаграмму комфортно употреблять для демонстрации связи меж данными, находящимися в различных рядах. Их можно показать в виде одной последовательности точек.

Точечная диаграмма в Excel (либо точечный график) нередко употребляется для сопоставления пар значений на координатной плоскости либо нахождения зависимости меж ними.

В качестве примера можно привести построение графиков функций либо, к примеру, график зависимости затраченного работникам компаниии времени на общение с клиентами по телефону и количеством решенных заморочек клиентов.
Давайте на данном примере разберем все шаги построения точечной диаграммы.

Как выстроить точечный график в Excel?

Представим, что у нас имеется таблица с 2-мя рядами данных (затраченное время и количество решенных вопросцев):

В левом столбце представлены данные по времени, которые сотрудники уделяют общению с клиентами, соответственно, в правом — данные по количеству решенных заморочек за уделенное время.
Чтоб выстроить точечную диаграмму, выделяем спектр с данными (A1:B10) и на панели вкладок избираем Вставка -> Диаграмма -> Точечная -> Точечная с маркерами:

В итоге получаем обычную диаграмму последующего вида:

Точечный график построен, сейчас настраиваем наружный вид диаграммы под свои предпочтения (добавляем наименования осей, диаграммы, избираем цвета линий и т.д.):

Если нужно выстроить точечную диаграмму с соединением точек линиями, то кроме обычного вида точечного графика также выделяют еще 4 типа точечных диаграмм:

• С маркерами — точки выделяются в виде маркеров;
• С гладкими кривыми и маркерами — диаграмма с соединением точек гладкими кривыми и выделением точек маркерами;
• С гладкими кривыми — диаграмма с соединением точек гладкими кривыми;
• С прямыми отрезками и маркерами — диаграмма с соединением точек прямыми отрезками и выделением точек маркерами;
• С прямыми отрезками — диаграмма с соединением точек прямыми отрезками.

Фортуны для вас и до скорой встречи на страничках блога Tutorexcel.ru!

Как выстроить график в Excel — задачка легкая, но новичков иногда сбивает с толку, какой тип диаграммы избрать либо как верно выстроить таблицу данных.

Итак, Excel дает два типа диаграмм для построения графика —

1. точечную диаграмму — употребляется, когда есть хотя бы два ряда, данные 1-го из их употребляются для определения второго. Пример — обычная функция y=x^2.
2. график — в случае, когда необходимо просто поглядеть как меняется ряд данных.

Построение диаграммы «график»

Давайте построим поначалу график, он строится весьма просто, фактически в одно-два касания. Используем данные о курсе бакса за декабрь 2013 г.

1. Выделяем таблицу, при всем этом даты будут применены в качестве подписей данных. Если же вы желаете, чтоб подписей не было (поточнее будут порядковые номера точек — 1,2,3…), то выделяйте лишь данные о курсах валют.
2. На вкладке «Вставка» есть целая панель диаграмм

Нажимаете клавишу «График».

Посреди их можно избрать тот, что больше подступает для ваших целей. Но потому что нам нужен просто ряд конфигурации по времени, то избираем либо 1-ый график либо аналогичный с маркерами. Я избрал с маркерами, т.к. у нас не настолько не мало данных.

График опосля первого шага

Настройка подписей графика

Я меняю заглавие диаграммы, осей, легенду убираю, т.к. у нас одна кривая, легенда нужна для 2-ух и больше, чтоб различать данные. Еще я добавлю главные полосы по вертикали, так нагляднее. Остальное не критично.

График с трендом

В принципе, все. Сейчас поглядим как создать график через точечную диаграмму.

Построение точечной диаграммы

Обычно, точечная диаграмма употребляется для построения графиков функций. К примеру, возьмем функцию y=x^2.

Построим таблицу данных из 2-ух столбцов.

Таблица данных y=x^2

Виды точечных диаграмм

График, построенный с помощью точечной диаграммы

2-ая таблица данных

Окно выбора данных

Корректировка данных рядов

Можно поставить свое случайное заглавие ряда. Если вдруг Excel ошибочно брал некий ряд в качестве независящей либо зависимой переменной, можно произвольно найти нужные спектры.

Здесь пятиминутное видео:

Для большей инфы предлагаю поглядеть пример построения .

«Глаза страшатся, а руки делают»

P.S. Приглянулась статья? Подпишитесь на рассылку в правой части странички (Бесплатный курс «Топ-10 инструментов Excel») и будьте в курсе новейших событий.

Навигация по записям ← Среднее значение в Excel Как включить макросы в Excel →

Интерполяция данных: соединяем точки так, чтоб было прекрасно

Как выстроить график по n точкам? Самое обычное — отметить их маркерами на координатной сетке. Но для наглядности их охото соединить, чтоб получить просто читаемую линию. Соединять точки проще всего отрезками прямых. Но график-ломаная читается достаточно тяжело: взор цепляется за углы, а не скользит вдоль полосы. Ну и смотрятся изломы не весьма прекрасно. Выходит, что не считая ломаных необходимо уметь строить и кривые. Но здесь необходимо быть усмотрительным, чтоб не вышло вот такового:

Мало матчасти

Восстановление промежных значений функции, которая в данном случае задана таблично в виде точек P₁&nbsp. &nbspP_n, именуется интерполяцией. Есть огромное количество методов интерполяции, но они все могут быть сведены к тому, что нужно отыскать n&nbsp–&nbsp1 функцию для расчёта промежных точек на соответственных секторах. При всем этом данные точки непременно должны быть вычислимы через надлежащие функции. На базе этого и быть может построен график:

Функции f_i могут быть самыми различными, но почаще всего употребляют полиномы некой степени. В этом случае итоговая интерполирующая функция (кусочно данная на промежутках, ограниченных точками P_i) именуется сплайном.

В различных инструментах для построения графиков — редакторах и библиотеках — задачка «прекрасной интерполяции» решена по-разному. В конце статьи будет маленький обзор имеющихся вариантов. Почему в конце? Чтоб опосля ряда приведённых выкладок и раздумий можно было поугадывать, кто из «серьёзных ребят» какие способы употребляет.

Ставим опыты

Самый обычной пример — линейная интерполяция, в которой употребляются полиномы первой степени, а в итоге выходит ломаная, соединяющая данные точки.
Давайте добавим незначительно конкретики. Вот набор точек (взяты практически с потолка):

Итог линейной интерполяции этих точек смотрится так: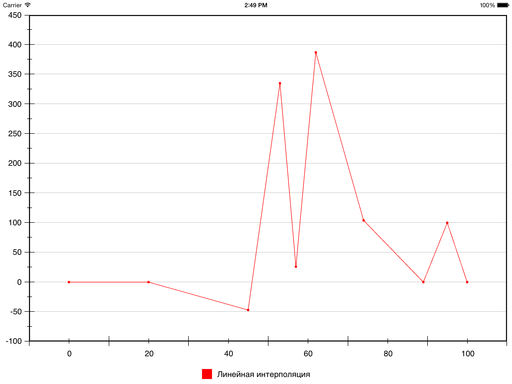

Но, как отмечалось выше, время от времени охото получить в итоге гладкую кривую.

Что есть гладкость? Бытовой ответ: отсутствие острых углов. Математический: непрерывность производных. При всем этом в арифметике гладкость имеет порядок, равный номеру крайней непрерывной производной, и область, на которой эта непрерывность сохраняется. Другими словами, если функция имеет гладкость порядка 1 на отрезке [a;&nbspb], это значит, что на [a;&nbspb] она имеет непрерывную первую производную, а вот 2-ая производная уже терпит разрыв в каких-либо точках.
У сплайна в контексте гладкости есть понятие недостатка. Недостаток сплайна — это разность меж его степенью и его гладкостью. Степень сплайна — это наибольшая степень использованных в нём полиномов.
Принципиально отметить, что «небезопасными» точками у сплайна (в которых может нарушиться гладкость) являются как раз P_i, другими словами точки сочленения частей, в которых происходит переход от 1-го полинома к другому. Все другие точки «неопасны», ведь у полинома на области его определения нет заморочек с непрерывностью производных.
Чтоб достигнуть гладкой интерполяции, необходимо повысить степень полиномов и подобрать их коэффициенты так, чтоб в граничных точках сохранялась непрерывность производных.

Обычно для решения таковой задачки употребляют полиномы третьей степени и достигают непрерывности первой и 2-ой производной. То, что выходит, именуют кубическим сплайном недостатка 1. Ах так он смотрится для наших данных:

Кривая, вправду, гладкая. Но если представить, что это график некого процесса либо явления, который необходимо показать заинтересованному лицу, то таковой способ, быстрее всего, не подступает. Неувязка в неверных экстремумах. Возникли они из-за очень мощного искривления, которое было призвано обеспечить гладкость интерполяционной функции. Но зрителю такое поведение совершенно не к слову, ведь он оказывается околпачат относительно пиковых значений функции. А ради приятной визуализации этих значений, фактически, всё и затевалось.
Так что нужно находить остальные решения.

Другое обычное решение, не считая кубических сплайнов недостатка 1 — полиномы Лагранжа. Это полиномы степени n&nbsp–&nbsp1, принимающие данные значения в данных точках. Другими словами членения на сегменты тут не происходит, вся последовательность описывается одним полиномом.
Но вот что выходит: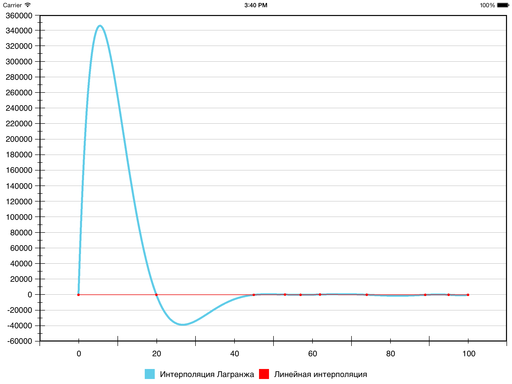

Гладкость, естественно, находится, но наглядность пострадала так очень, что… пожалуй, стоит выискать остальные способы. На неких наборах данных итог выходит обычный, но в общем случае ошибка относительно линейной интерполяции (и, соответственно, неверные экстремумы) может получаться очень большенный — из-за того, что здесь всего один полином на все сегменты.

В компьютерной графике весьма обширно используются кривые Безье, выставленные полиномами k-й степени.
Они не являются интерполирующими, потому что из k&nbsp+&nbsp1 точек, участвующих в построении, итоговая кривая проходит только через первую и последнюю. Другие k&nbsp–&nbsp1 точек играют роль собственного рода «гравитационных центров», притягивающих к для себя кривую.
Вот вам наглядный пример кубической кривой Безье:

Как это можно употреблять для интерполяции? На базе этих кривых тоже можно выстроить сплайн. Другими словами на любом секторе сплайна будет своя кривая Безье k-й степени (к слову, k&nbsp=&nbsp1 даёт линейную интерполяцию). И вопросец лишь в том, какое k взять и как отыскать k&nbsp–&nbsp1 промежную точку.
Тут нескончаемо много вариантов (так как k ничем не ограничено), но мы разглядим традиционный: k&nbsp=&nbsp3.
Чтоб итоговая кривая была гладкой, необходимо достигнуть недостатка 1 для составляемого сплайна, другими словами сохранения непрерывности первой и 2-ой производных в точках сочленения частей (P_i), как это делается в традиционном варианте кубического сплайна.
Решение данной задачки тщательно (с начальным кодом) рассмотрено тут.
Вот что получится на нашем тестовом наборе:

Сделалось лучше: неверные экстремумы всё ещё есть, но хотя бы не так очень различаются от настоящих.

Думаем и экспериментируем

Можно испытать ослабить условие гладкости: востребовать недостаток 2, а не 1, другими словами сохранить непрерывность одной лишь первой производной.
Достаточное условие заслуги недостатка 2 в том, что промежные контрольные точки кубической кривой Безье, смежные с данной точкой интерполируемой последовательности, лежат с данной точкой на одной прямой и на схожем расстоянии:

В качестве прямых, на которых лежат точки C_{i&nbsp–&nbsp1} (2) , P_i и C_i (1) , целенаправлено взять касательные к графику интерполируемой функции в точках P_i. Это гарантирует отсутствие неверных экстремумов, потому что кривая Безье оказывается ограниченной ломаной, построенной на её контрольных точках (если эта ломаная не имеет самопересечений).

Способом проб и ошибок эвристика для расчёта расстояния от точки интерполируемой последовательности до промежной контрольной вышла таковой:

1-ая и крайняя промежные контрольные точки равны первой и крайней точке графика соответственно (точки C₁ (1) и C_{n&nbsp–&nbsp1} (2) совпадают с точками P₁ и P_n соответственно).
В этом случае выходит вот таковая кривая:

Как видно, неверных экстремумов уже нет. Но если ассоциировать с линейной интерполяцией, местами ошибка весьма большая. Можно создать её ещё меньше, но здесь в ход пойдут ещё наиболее хитрые эвристики.

К текущему варианту мы пришли, уменьшив гладкость на один порядок. Можно создать это ещё раз: пусть сплайн будет иметь недостаток 3. По факту, тем формально функция не будет гладкой совершенно: даже 1-ая производная может вытерпеть разрывы. Но если рвать её аккуратненько, зрительно ничего ужасного не произойдёт.
Отказываемся от требования равенства расстояний от точки P_i до точек C_{i&nbsp–&nbsp1} (2) и C_i (1) , но при всем этом сохраняем их все лежащими на одной прямой: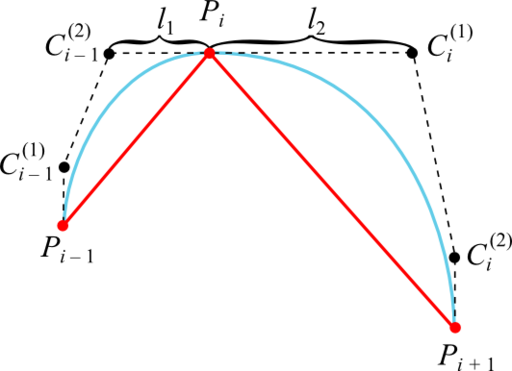

Эвристика для вычисления расстояний будет таковой:

Итог выходит таковой: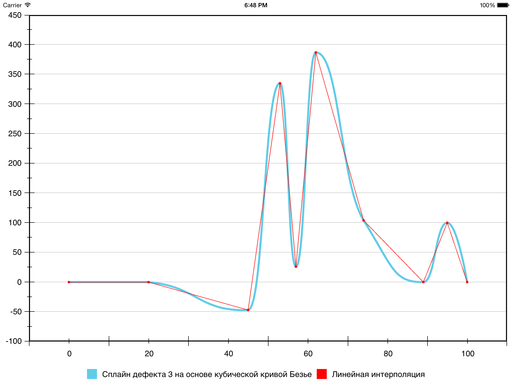

В итоге на шестом секторе ошибка уменьшилась, а на седьмом — возросла: кривизна у Безье на нём оказалась больше, чем хотелось бы. Поправить ситуацию можно, принудительно уменьшив кривизну и тем «прижав» Безье поближе к отрезку прямой, которая соединяет граничные точки сектора. Для этого употребляется последующая эвристика:

Итог последующий: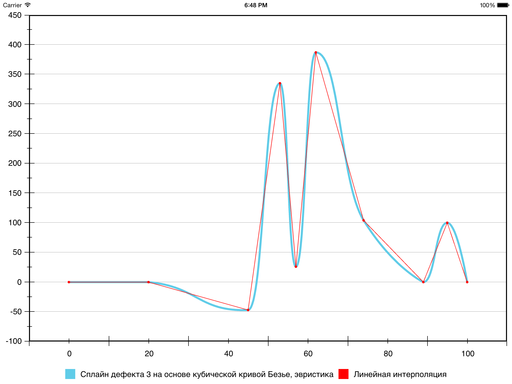

На этом было принято решение признать цель достигнутой.
Быть может, кому-то понадобится код.

Как люди-то делают?

Обещанный обзор. Естественно, перед решением задачки мы поглядели, кто чем может повытрепываться, а уже позже начали разбираться, как создать самим и по способности лучше. Но ах так лишь сделали, не без наслаждения ещё раз прошлись по легкодоступным инструментам и сравнили их результаты с плодами наших тестов. Итак, поехали.

MS Excel

Это весьма похоже на рассмотренный выше сплайн недостатка 1, основанный на кривых Безье. Правда, в отличие от него в чистом виде, здесь всего два неверных экстремума — 1-ый и 2-ой сегменты (у нас было четыре). Видимо, к традиционному поиску промежных контрольных точек здесь добавляются ещё какие-то эвристики. Но ото всех неверных экстремумов они не выручили.

LibreOffice Calc

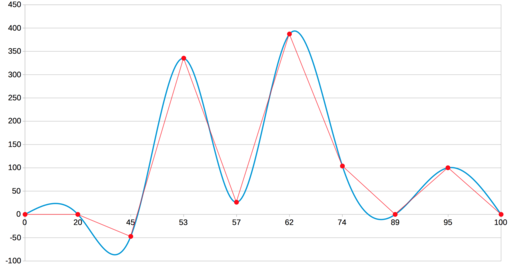
В настройках это названо кубическим сплайном. Разумеется, он тоже основан на Безье, и вот здесь уже четкая копия нашего результата: все четыре неверных экстремума на месте.

Есть там ещё один тип интерполяции, который мы здесь не разглядывали: B-сплайн. Но для нашей задачки он очевидно не подступает, потому что даёт вот таковой итог 🙂

Highcharts, одна из самых фаворитных JS-библиотек для построения диаграмм

Здесь налицо «способ касательных» в варианте равенства расстояний от точки интерполируемой последовательности до промежных контрольных. Неверных экстремумов нет, зато есть сравнимо большая ошибка относительно линейной интерполяции (седьмой сектор).

amCharts, ещё одна пользующаяся популярностью JS-библиотека

Картина весьма похожа на экселевскую, те же два неверных экстремума в тех же местах.

Coreplot, самая пользующаяся популярностью библиотека построения графиков для iOS и OS X

Есть неверные экстремумы и видно, что употребляется сплайн недостатка 1 на базе Безье.
Библиотека открытая, так что можно поглядеть в код и убедиться в этом.

aChartEngine, вроде как самая пользующаяся популярностью библиотека построения графиков для Android

Больше всего похоже на кривую Безье степени n&nbsp–&nbsp1, хотя в самой библиотеке график именуется «cubic line». Удивительно! Вроде бы то ни было, здесь не только лишь находятся неверные экстремумы, да и в принципе не производятся условия интерполяции.