12. Точечная и пузырьковая диаграммы

Точечные и пузырьковые диаграммы почти во всем похожи: они употребляют XY-график для визуализации содержимого таблицы. Но диаграммы различаются стилем маркером для отдельных точек данных.

Таблица точечной диаграммы организована последующим образом, при всем этом любая строчка представляет одну точку данных:

Таблица пузырьковой диаграммы содержит значения в столбце Размер , а в остальном организована таковым же образом:

Столбец Группа таблицы можно применять для объединения отдельных точек данных в группы. В таблице точечной диаграммы выше 1-ые три точки данных принадлежат группе A, а оставшиеся точки данных — группе B. Вы сможете просто избрать несколько точек данных, принадлежащие одной группе, нажав на точку данных и переместив указатель мыши, удерживая кнопку Shift (см. раздел Множественный выбор).

Оси точечных и пузырьковых диаграмм также можно настроить. Доп сведения см. в разделе Шкалы и оси. Вы также сможете применять даты для значений X и Y. Если все ячейки в таблице для одной оси содержат даты, и в качестве формата ячейки Excel избран параметр Дата , в подписях делений оси показываются даты и вы сможете отформатировать их подходящим образом (см. раздел Отран управления форматом дат).

Если избран параметр Применять функцию «Заполнять сверху» Excel (см. раздел Цветовая схема), в качестве цвета заливки можно избрать цвет из характеристик форматирования Excel в хоть какой ячейке в строке точки данных, чтоб задать цвет для маркера данной точки данных.

12.1 Метки

На обоих типах диаграмм с каждой точкой данных можно связать до 2-ух меток. Метки можно добавить при помощи клавиши

Добавить метку и удалить при помощи клавиши

Удалить метки . Отран управления содержимым метки дозволяет избрать формат текстового поля для каждой метки, чтоб показывать текст метки, также значения X, Y и размера (см. раздел Содержимое меток). По дефлоту метки отключены для диаграмм, содержащих наиболее 300 точек данных. По мере необходимости их можно включить в контекстном меню.

Автоматическое средство прибавления меток располагает метки очень близко к их точкам данных, используя соединительные полосы, по мере необходимости (см. раздел Автоматическое размещение меток).

Когда средство занимается расчетом позиций меток, в левом верхнем углу диаграммы возникает крутящийся значок хода выполнения

, а соответственная диаграмма выделяется серой рамкой. Вы сможете сохранить файл либо продолжить работу с иными диаграммами и слайдами, пока средство не окончит работу.

В редчайших вариантах средство может не отыскать лучшую позицию для всех меток. В данной ситуации вы сможете вручную расположить метки. Попытайтесь вручную расположить одну из некорректно расположенных меток и разрешите средству автоматом расположить оставшиеся метки. Обычно для рационального размещения меток можно вручную расположить всего несколько из проблемных меток.

12.2 Точечная диаграмма

Точечная диаграмма употребляет отран управления схемой маркера для согласованной маркировки точек данных, принадлежащих одной группе (см. раздел Схема метки). Отран управления фигурой маркера можно применять для выбора фигуры маркера для отдельных точек данных (см. раздел Фигура метки).

Если избрать параметр Без маркеров в элементе управления схемой маркера, то маркеры для точек данных будут отключены. В этом случае метки выравниваются по центру позиции точек данных. Но при автоматическом размещении метки могут сместиться от данной позиции для предотвращения наложения.

Нереально отключить маркер и скрыть метку для точки данных.

12.3 Пузырьковая диаграмма

Пузырьковая диаграмма — это вариант точечной диаграммы, точки данных в которой обозначены кругами. Размер кругов определяется значениями в столбце Размер . По дефлоту значение столбца Размер пропорционально площади круга. Клавиша

Создать поперечник подходящим размеру в контекстном меню дозволяет установить значение столбца Размер как пропорциональное поперечнику всякого круга.

Чтоб включить условные обозначения размера пузырьков, нажмите

Добавить условные обозначения размера пузырьков в контекстном меню диаграммы. Чтоб поменять размер пузырьков, применяемый в условных обозначениях, изберите пузырек и перетащите маркер, который отображается на правой границе.

Если избрать один из пузырьков на диаграмме, аналогичный маркер покажется на правой границе. Чтоб поменять размер пузырька, перетащите маркер. Все остальные пузырьки будут масштабированы подходящим образом, так как отношение меж пузырьками постоянно определяется значениями в столбце Размер в таблице.

Если два пузырька перекрываются, наиболее маленький пузырек отображается перед наиболее большим. Чтоб поменять порядок, изберите

На фронтальный план в контекстном меню пузырька.

12.4 Линия тренда и раздел

12.4.1 Линия тренда

Для точечных и пузырьковых диаграмм think-cell может вычислять полосы тренда для группы значений. Линия тренда — это графическое представление трендов в группе. Они употребляются для исследования заморочек прогнозирования, которые также именуют регрессионных анализом.

Линия тренда рассчитывается при помощи линейной регрессии, чтоб сумма всех точек квадратичной различия меж координатой Y и значением полосы тренда в координате X была малой. На пузырьковой диаграмме размер пузырьков употребляется для оценки вклада каждой точки в разницу.

Линию тренда можно добавить на диаграмму 2-мя методами.

Нажмите правой клавишей мыши на маркер либо пузырек подходящей группы и изберите

Вы сможете избрать тип полосы тренда в элементе управления типом полосы тренда на соответственной контекстной панели инструментов. Тип Линейный употребляется по дефлоту и постоянно доступен. Когда на точечной диаграмме линия тренда рассчитывается на базе определенной группы (флаг Все группы не установлен), а цвет заливки и разрывы осей не употребляются, доступны доп типы линий тренда.

• Степенной : идеальнее всего подступает при наличии степенного дела меж значениями Y и X.
• Экспоненциальный : идеальнее всего подступает для экспоненциальных отношений.
• Логарифмический : идеальнее всего подступает для логарифмических отношений.

В последующем примере показано применение Степенной полосы тренда на точечной диаграмме, на которой значения Y — это квадрат значений X:

Вы сможете поменять цвет фона сбоку от полосы и переместить линию так же, как линию раздела (см. раздел Раздел). Но опосля перемещения полосы она больше не будет рассчитываться на базе значений в таблице.

12.4.2 Раздел

Вы сможете добавить линию раздела на точечные и пузырьковые диаграммы, чтоб она указывала на раздел набора. Чтоб добавить линию раздела, изберите

Добавить линию тренда/раздел в контекстном меню диаграммы.

Чтоб переместить линию, нажмите и перетащите ее в необходимое пространство. Вы также сможете избрать линию раздела и перетащить маркеры в начало либо конец полосы раздела. При перетаскивании концы будут прикрепляться к требуемым значениям. Интервал точек прикрепления зависит от текущего уровня масштаба. Если задерживать кнопку Shift во время перетаскивания, угол полосы раздела ограничен текущим углом либо вертикальной, горизонтальной и диагональной линией.

Чтоб сделать копию линию раздела, удерживайте кнопку Ctrl во время перетаскивания. Это обычной метод сделать параллельные полосы, к примеру для обозначения спектра значений.

Вы сможете поменять цвет фона набора, нажав на линию раздела и выбрав цвет фона на панели инструментов. Чтоб установить цвет фона области с иной стороны полосы, нажмите правой клавишей мыши на линию раздела и изберите

Перевернуть сторону заливки . Вы также сможете просто два раза надавить на линию раздела.

Чтоб вычислить позицию и угол полосы на базе значений на диаграмме, изучите раздел Линия тренда.

Пузырьковая диаграмма в работе маркетолога

Всем, привет! Сейчас разглядим пример использования пузырьковой диаграммы в работе маркетолога.

«Так-так, ну и какую же комбинацию продуктового ранца избрать в различных магазинах городка, какие продукты дадут огромную прибыль нашей компании, а какие стоит и совсем исключить из продуктовой линейки? Как очень влияет количество возвратов на прибыльность определенного магазина сети?», — задумывался рекламщик Василий и находил ответы на свои вопросцы…

Василий недельку вспять пришел в компанию и лишь заходил в курс дел, но уже на данный момент ему необходимо было проявить себя и предложить конфигурации в структуре продуктового ранца, которые посодействовали бы повысить прибыльность компании и ее магазинов.

В состав продуктового ранца входило наиболее 200 единиц продукции, посреди которых имелись очевидные фавориты рынка. При всем этом был и ряд продуктов, которые покупатели нередко возвращали назад в магазин. А рекламщик Василий все размышлял: «Как неловко представлены все данные на данный момент, в этих массивных таблицах – разобраться с ситуацией в таком виде весьма трудно. Совершенно точно, мне нужен таковой тип визуализации, чтоб оперативно выделить ТОПы продаж и те продукты, что лишь распыляют ресурсы компании. А что? Bubble Chart – вот одно из вероятных решений таковой задачки».

Итак, задачка маркетолога Василия:

проанализировать реализации в разных магазинах сети с учетом прибыльности и возвратов для оптимизации продуктового ранца.

Дальше я расскажу, как рекламщик Василий решил задачку, но для начала – маленькая вводная часть о том, что такое пузырьковая диаграмма, и для каких целей она может употребляться.

Пузырьковая диаграмма: минута теории

Пузырьковая диаграмма: Что же все-таки это такое?

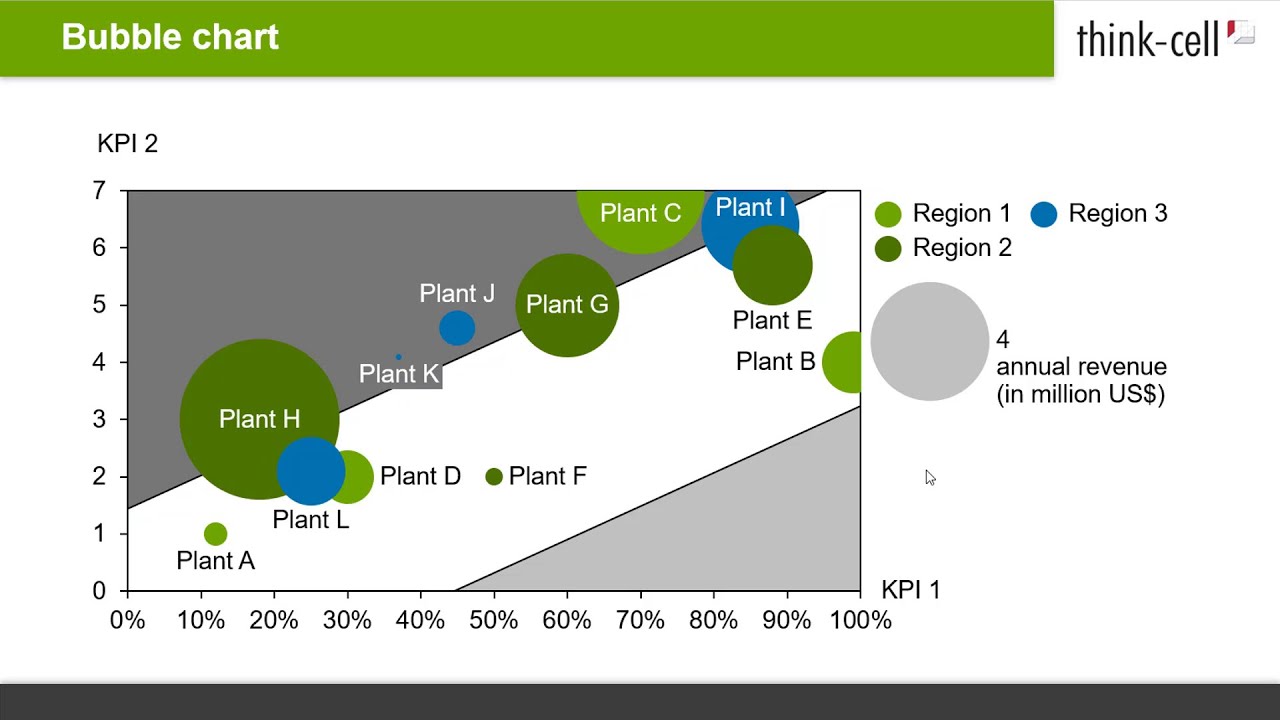
Разноцветные круги, разбросанные на координатной плоскости, именуются Bubble Chart либо пузырьковая диаграмма (подвид диаграммы рассеяния):

На пузырьковой диаграмме точки с данными представлены в виде «пузырей», что дозволяет сразу показывать до 4 метрик: две отвечают за положение по осям X и Y, одна за размер и ещё одна за цвет пузыря. Размер и цвет кругов помогает задать доп переменные для анализа.

Пузырьковая диаграмма: Когда используем?

Пузырьковая диаграмма приходит на помощь, когда необходимо найти вид и тесноту связи меж парами соответственных переменных, другими словами узреть корреляцию меж тремя-четырьмя величинами либо отыскать аналогию в огромных наборах данных.

Пузырьковая диаграмма непревзойденно подступает для выявления «мощного и слабенького звена»: более и менее удачных магазинов в сети, низкомаржинальной группы продуктов с маленьким объемом продаж и т.д.

Пузырьковая диаграмма : анализ магазинов

А вот сейчас вернемся к маркетологу Василию. Он сделал пузырьковую диаграмму по магазинам сети с таковыми измерениями:

• Ось Х: реализации,
• Ось У: прибыль,
• Размер: толика магазина в общей прибыли,
• Цвет: толика возвращенных продуктов.

Вот какая визуализация у него вышла:

Построив пузырьковую диаграмму (даже при наличии огромного количества частей), рекламщик Василий сходу узрел, что в части магазинов уровень прибыльности ниже при довольно высочайшем объеме продаж. Доп измерение, толика возвращенных продуктов, подтвердила его опаски – в магазинах с низкой прибылью толика возвратов еще выше, чем в среднем по сети. Другими словами магазин несет значительные затратные расходы, при всем этом в итоге принося не весьма огромную прибыль.

Посреди магазинов с высочайшими показателями продаж часть также выбивается по показателю толики возвратов. Потому Василий перебежал на остальные вкладки QlikView, где проанализировал, какие продукты, из каких партий поставок и в каком регионе возвращают почаще всего, и занес свое 1-ое предложение по оптимизации ассортимента. Но это уже, как говорится, совершенно иная история…

А на данный момент расскажу о том, как сделать пузырьковую диаграмму в QlikView.

Пузырьковая диаграмма в QlikView по шагам

Пузырьковую диаграмму в QlikView сделать просто, но лишь если знаешь как. Вот пара вопросцев, с которыми необходимо обусловиться для начала:

1. «Что фактически должен показывать пузырь на диаграмме?»

Ответом на этот вопросец будет измерение. Да, конкретно измерение, не удивляйтесь.

Дело в том, что в большинстве диаграмм QlikView измерение соответствует осям диаграммы, но не в случае пузырьковой диаграммы. Тут логическое измерение – не то же самое, что графическое.

1. «Где должен размещаться пузырь?»

Ответом на этот вопросец станут меры, которые будут привязаны к осям диаграмм, также размеру и цвету пузырей (в случае, если мер у Вас будет наиболее 2-ух).

Как вы обусловились с измерениями и выражениями, приступаем к созданию пузырьковой диаграммы:

1. Объект –> Новейший объект листа -> Диаграмма
2. Избираем Точечная диаграмма (Scatter Chart), ведь пузырьковая диаграмма – разновидность точечной. Жмем клавишу «Дальше».
3. Добавляем измерение и жмите клавишу «Дальше».
4. Добавляем поля, которые вы желаете применять для 2-ух ваших выражений по осям X и Y.
5. Пока это точечная диаграмма. Для того, чтоб она стала пузырьковой, добавляем третье измерение, которое описывает размер пузырей.
6. Открываем Расширенный режим (Advanced Mode). Тут QlikView перескакивает на страничку сортировки, потому жмем «Вспять», чтоб проверить, верны ли функции агрегирования для ваших выражений. Может быть, для вас пригодиться поменять их.
7. Когда мы все проверили, жмем клавишу «Готово».

Итак, наша пузырьковая диаграмма сотворена. Чтоб создать ее наиболее комфортной для восприятия, Вы сможете мало поработать с ее стилем (Style):

• Избираем Вид отображения частей диаграммы (Style – Look). Рекомендую применять вид пузырей без размера – это облегчит восприятие данных для бизнес-пользователей.
• Увеличиваем размер пузырей в свойствах объекта во вкладке Представление задаем наибольшее значение пузыря, к примеру 32 пт (Presentation – Max bubble size).
• Изменяем масштаб одной либо 2-ух осей (Axes – Scale)

Пузырьковая диаграмма: на что направить внимание

Опосля сотворения диаграммы, смотрим на нее исходя из убеждений другого человека. Понятна ли она?

Не забываем про:

• заглавие диаграммы;
• интервал времени;
• наименования и единицы измерения каждой оси.

П.С. На закуску – пузырьковая диаграмма по пищевым добавкам и их воздействию на здоровье человека. А что? У пузырьковых диаграмм весьма широкий диапазон внедрения.

Поведайте в комментах, как вы используете пузырьковые диаграммы в работе.

Внедрение точечных диаграмм для визуализации данных

Привет, Хабр! Представляю вашему вниманию перевод статьи «Everything you need to know about Scatter Plots for Data Visualisation» создателя George Seif.

Если вы занимаетесь анализом и визуализацией данных, то быстрее Для вас придется столкнуться с точечными диаграммами. Невзирая на свою простоту, точечные диаграммы являются массивным инвентарем для визуализации данных. Манипулируя цветами, размерами и формами можно обеспечить упругость и репрезентативность точечных диаграмм.

В данной статье вы узнаете фактически все, что для вас нужно знать о визуализации данных используя точечные диаграммы. Мы попытаемся разобрать все нужные характеристики в их использовании в коде python. Также вы сможете отыскать несколько практических уловок.

Построение регрессии

Даже самое примитивное внедрение точечной диаграммы уже дает сносный обзор наших данных. На рисунке 1 мы уже можем созидать островки объединённых данных и стремительно выделить выбросы.

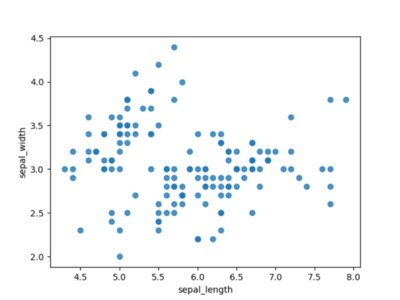
Набросок 1

Уместно проведенные регрессионные линий зрительно упрощает задачку выявления точек, близких к середине. На рисунке 2 мы провели линейный график. Достаточно просто узреть, что в данном случае линейная функция не репрезентативен, так как почти все точки находятся достаточно далековато от полосы.

Набросок 2

Набросок 3 употребляет полином порядка 4 и смотрится еще наиболее многообещающе. Похоже, что для моделирования этого набора данных нам точно пригодится полином порядка 4.

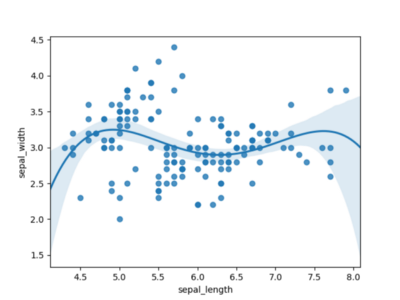
Набросок 3

Цвет и форма точек

Цвет и форму можно применять для визуализации разных категорий в вашем наборе данных. Цвет и форма зрительно весьма понятны. Когда вы смотрите на график, где группы точек имеют различные цвета наших фигур, сходу становится естественным, что точки принадлежат различным группам.

На рисунке 4 показаны классы, сгруппированные по цвету. На рисунке 5 показаны классы, разбитые по цвету и форме. В обоих вариантах намного легче узреть группировку. Сейчас мы знаем, что будет просто отделить класс setosa, и на что мы должны сосредоточить внимание. Также ясно, что один линейный график не сумеет поделить зеленоватую и оранжевую точки. Потому нам необходимо добавить что-то для отображения больше измерений.

Выбор меж цветом и формой становится вопросцем предпочтения. Лично я нахожу цвет мало наиболее точным и интуитивно понятным, но выбор остается постоянно за Вами.

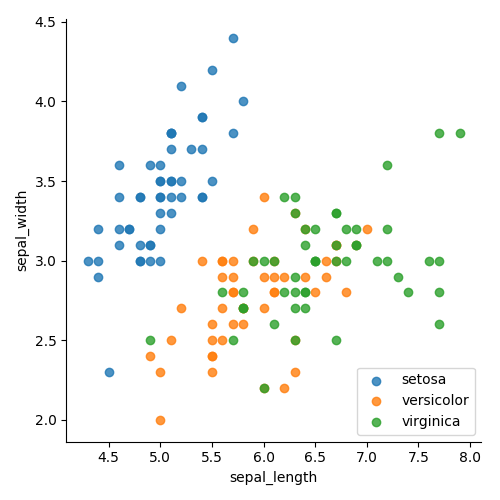
Набросок 4

Набросок 5

Маргинальная гистограмма

Пример графика с маргинальными гистограммами показан на рисунке 6. Маргинальные гистограммы наложены сверху и сбоку, представляют собой распределение точек для объектов вдоль абсциссы и ординате. Это маленькое дополнение непревзойденно подступает для наиболее четкого определения распределения точек и выбросов.

К примеру, на рисунке 6 мы разумеется лицезреем высшую концентрацию точек около разметки 3,0. И благодаря данной гистограмме можно найти уровень концентрации. В правом боку видно, что вокруг разметки 3,0 есть как минимум в три раза больше точек, чем для хоть какого другого дискретного спектра. Также при помощи правой боковой гистограммы можно с очевидностью распознать, что тривиальные выбросы находятся выше отметки 3,75. По верхней диаграмме видно, что распределение точек по оси Х является наиболее равномерным, кроме выбросов в последнем правом углу.

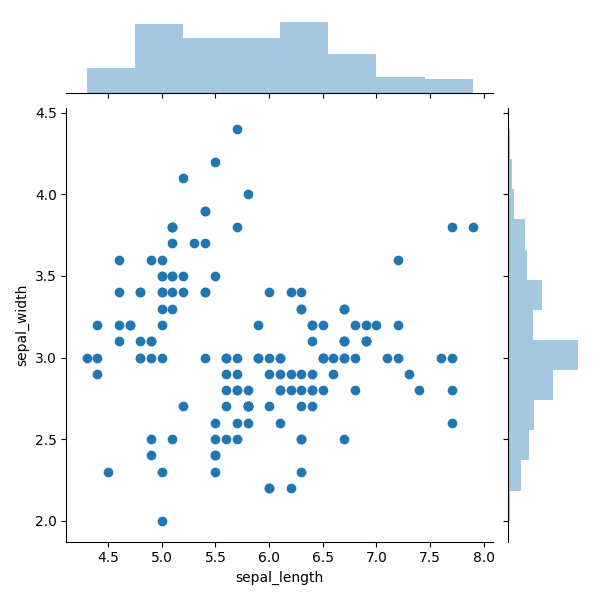
Набросок 6

Пузырьковые диаграммы

При помощи пузырьковых диаграмм нам нужно применять несколько переменных для кодировки инфы. Новеньким параметром, характерный для этого вида визуализацией, является размер. На рисунке 7 мы показываем количество съеденного картофеля фри разрезе роста и веса съевших людей. Направьте внимание, что точечная диаграмма — это всего только инструмент двухмерной визуализации, но при использовании пузырьковых диаграмм мы искусно можем показывать информацию с 3-мя измерениями.

Тут мы используем цвет, положение и размер, где положение пузырьков описывает рост и вес человека, цвет описывает пол, а размер определяется количеством съеденной картошки фри. Пузырьковая диаграмма с легкостью дозволяет нам комфортно соединить все атрибуты в один график, чтоб мы могли созидать информацию огромного размера в двухмерном виде.

Набросок 7