Решение уравнений в excel; примеры решений

Решение уравнений в excel — примеры решений

Microsoft Office Excel может здорово помогать студентам и магистрантам в решении разных задач из высшей арифметики. Не почти все юзеры знают, что базисные математические способы поиска неведомых значений в системе уравнений реализованы в редакторе. Сейчас разглядим, как происходит решение уравнений в excel.

1-ый способ

Сущность этого метода заключается в использовании специального инструмента программки – подбор параметра. Отыскать его можно во вкладке Данные на Панели управления в выпадающем перечне клавиши Анализ «что-если».

1. Зададимся обычным квадратичным уравнением и найдем решение при х=0.

2. Перебегайте к инструменту и заполняете все нужные поля

3. Опосля проведения вычислений программка выдаст итог в ячейке с иксом.

4. Подставив приобретенное значение в начальное уравнение можно проверить корректность решения.

2-ой способ

Используем графическое решение этого же уравнения. Сущность заключается в том, что создается массив переменных и массив значений, приобретенных при решении выражения. Основываясь на этих данных, строится график. Пространство пересечения кривой с горизонтальной осью и будет неведомой переменной.

1. Создаете два спектра.

На заметку! Смена знака результата гласит о том, что решение находится в промежутке меж этими 2-мя переменными.

2. Перебегайте во вкладку Вставка и выбираете обыденный график.

3. Выбираете данные из столбца f (x), а в качестве подписи горизонтальной оси – значения иксов.

Принципиально! В настройках оси поставьте положение по делениям.

4. Сейчас на графике верно видно, что решение находится меж семеркой и восьмеркой поближе к 7. Чтоб выяснить наиболее четкое значение, нужно изменять масштаб оси и уточнять числа в начальных массивах.

Таковая экспериментальная методика в первом приближении является довольно грубой, но дозволяет узреть поведение кривой при изменении неведомых.

3-ий способ

Решение систем уравнений можно проводить матричным способом. Для этого в редакторе есть отдельная функция МОБР. Сущность заключается в том, что создаются два спектра: в один выписываются аргументы при неведомых, а во 2-ой – значения в правой стороне выражения. Массив аргументов трансформируется в оборотную матрицу, которая позже множится на числа опосля знака равно. Разглядим подробнее.

1. Записываете произвольную систему уравнений.

2. Раздельно выписываете аргументы при неведомых в каждую ячейку. Если нет какого-то из иксов – ставите ноль. Аналогично поступаете с цифрами опосля знака равно.

3. Выделяете в вольной зоне спектр ячеек равный размеру матрицы. В строке формул пишете МОБР и выбираете массив аргументов. Чтоб функция сработала корректно нажимаете сразу Ctrl+Shift+Enter.

4. Сейчас находите решение с помощью функции МУМНОЖ. Также за ранее выделяете спектр размером с матрицу результатов и нажимаете уже известное сочетание кнопок.

4-ый способ

Способом Гаусса можно решить фактически всякую систему уравнений. Сущность в том, чтоб пошагово отнять одно уравнение из другого умножив их на отношение первых коэффициентов. Это ровная последовательность. Для полного решения нужно еще провести оборотное вычисление до того времени, пока диагональ матрицы не станет единичной, а другие элементы – нулевыми. Приобретенные значения в крайнем столбце и являются разыскиваемыми неведомыми. Разглядим на примере.

Принципиально! Если 1-ый аргумент является нулевым, то нужно поменять строчки местами.

1. Зададимся случайной системой уравнений и выпишем все коэффициенты в отдельный массив.

2. Копируете первую строчку в другое пространство, а ниже записываете формулу последующего вида: =C67:F67-$C$66:$F$66*(C67/$C$66).

Так как работа идет с массивами, жмите Ctrl+Shift+Enter, заместо Enter.

3. Маркером автозаполнения копируете формулу в нижнюю строчку.

4. Выделяете две 1-ые строки новейшего массива и копируете их в другое пространство, вставив лишь значения.

5. Повторяете операцию для третьей строчки, используя формулу

=C73:F73-$C$72:$F$72*(D73/$D$72). На этом ровная последовательность решения закончена.

6. Сейчас нужно пройти систему в оборотном порядке. Используйте формулу для третьей строки последующего вида =(C78:F78)/E78

7. Для последующей строчки используйте формулу =(C77:F77-C84:F84*E77)/D77

8. В конце записываете вот такое выражение =(C76:F76-C83:F83*D76-C84:F84*E76)/C76

9. При получении матрицы с единичной диагональю, правая часть дает разыскиваемые неведомые. Опосля подстановки приобретенных цифр в хоть какое из уравнений значения по обе стороны от знака равно являются схожими, что гласит о правильном решении.

Способ Гаусса является одним из самых трудозатратных посреди иных вариантов, но дозволяет пошагово просмотреть процесс поиска неведомых.

Видите ли, существует несколько способов решения уравнений в редакторе. Но любой из их просит определенных познаний в арифметике и точного осознания последовательности действий. Но для упрощения можно пользоваться онлайн калькулятором, в который заложен определенный способ решения системы уравнений. Наиболее продвинутые веб-сайты предоставляют несколько методов поиска неведомых.

Отыскиваем наилучшее решение задачки с неведомыми параметрами в Excel

«Поиск решений» — функция Excel, которую употребляют для оптимизации характеристик: прибыли, плана продаж, схемы доставки грузов, рекламного бюджета либо рентабельности. Она помогает составить расписание служащих, распределить расходы в бизнес-плане либо вкладывательные вложения. Познание данной функции сберегает много времени и сил. Рассказываем, как освоить функцию поиска решений.

Главные характеристики поиска решений

Отыскать решение задачки можно 3-мя методами. Во-1-х, вручную перебирать характеристики, пока не найдется наилучшее соотношение. Во-2-х, составить уравнение с огромным количеством неведомых. В-третьих, вбить данные в Excel и применять «Поиск решений». Крайний метод самый резвый и покажет очень четкое решение, если знать, как применять функцию.

Итак, мы решаем задачку при помощи поиска решений в Excel и начинаем с математической модели. В ней четыре типа данных: константы, изменяемые ячейки, мотивированная функция и ограничения. К поиску решения вернемся чуток позднее, а на данный момент разберемся, что заходит в любой из этих типов:

Константы — начальная информация. К ней относится удельная маржинальная прибыль, стоимость каждой перевозки, нормы расхода товарно-материальных ценностей. В нашем случае — производительность работников, их оплата (выдача денег по какому-нибудь обязательству) и норма в 1000 изделий. Также константа отражает ограничения и условия математической модели: к примеру, лишь неотрицательные либо целые значения. Мы вносим константы в таблицу цифрами либо при помощи простых формул (СУММ, СРЗНАЧ).

Изменяемые ячейки — переменные, которые в итоге необходимо отыскать. В задачке это распределение 1000 изделий меж работниками с минимальными затратами. В различных вариантах бывает одна дифференцируемая ячейка либо спектр. При заполнении функции «Поиск решений» принципиально бросить ячейки пустыми — программка сама отыщет значения.

Мотивированная функция — результирующий показатель, для которого Excel подбирает лучшие характеристики. Чтоб программка соображала, какие данные лучшие, мы задаем функцию в виде формулы. Эту формулу мы отображаем в отдельной ячейке. Результирующий показатель может принимать наибольшее либо малое значения, также быть определенным числом.

Ограничения — условия, которые нужно учитывать при оптимизации функции, называющейся мотивированной. К ним относятся размеры инвестирования, срок реализации проекта либо размер покупательского спроса. В нашем случае — количество дней и число работников.

Пример использования поиска решений

Сейчас перейдем к самой функции.

1) Чтоб включить «Поиск решений», сделайте последующие шаги:

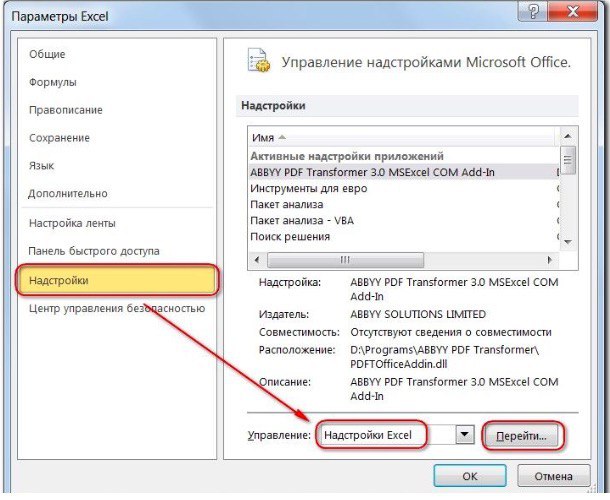
• нажмите «Характеристики Excel», а потом изберите категорию «Надстройки»;
• в поле «Управление» изберите значение «Надстройки Excel» и нажмите клавишу «Перейти»;
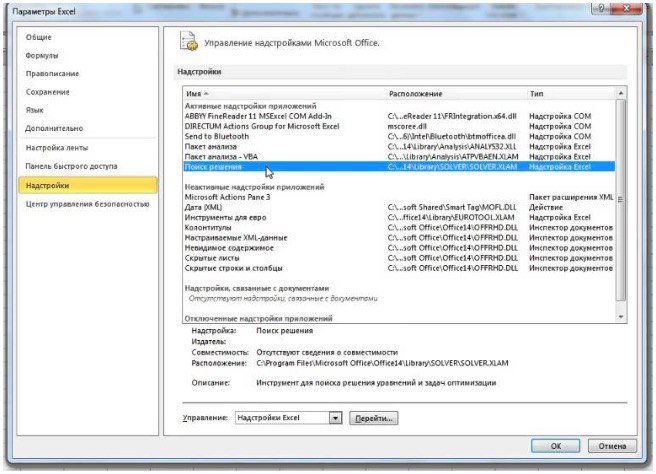
• в поле «Доступные надстройки» установите флаг рядом с пт «Поиск решения» и нажмите клавишу ОК.

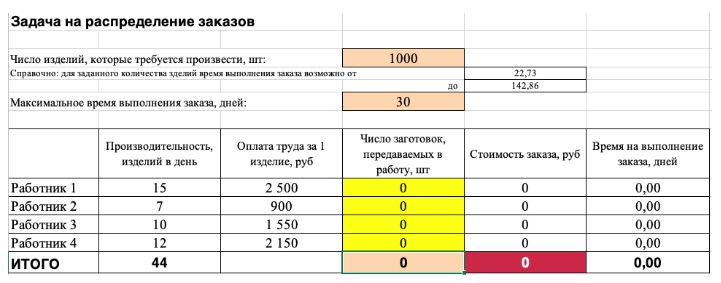
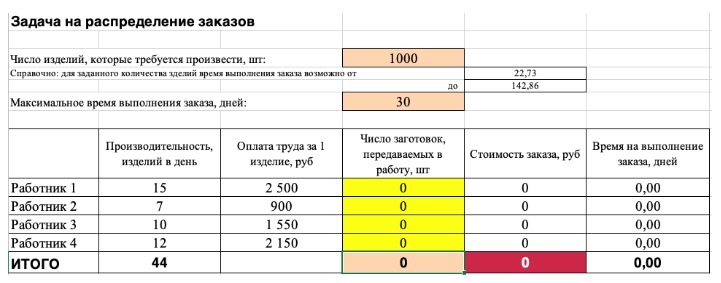
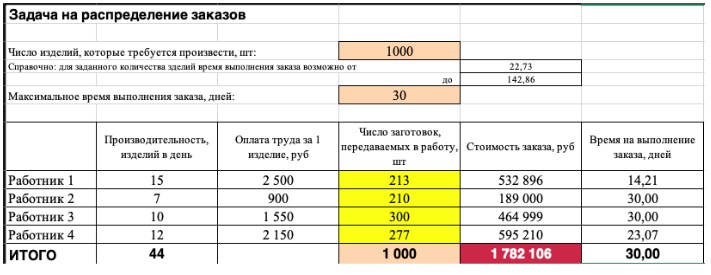
2) Сейчас упорядочим данные в виде таблицы, отражающей связи меж ячейками. Рекомендуем применять цветовые обозначения: на примере красноватым выделена мотивированная функция, бежевым — ограничения, а желтоватым — изменяемые ячейки.

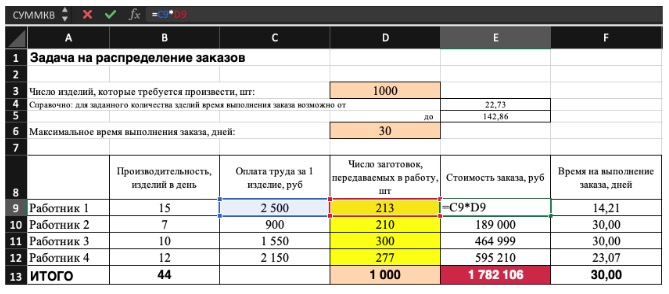
Не забудьте ввести формулы. Стоимость заказа рассчитывается как «Оплата (выдача денег по какому-нибудь обязательству) труда за 1 изделие» помножить на «Число заготовок, передаваемых в работу». Для того, чтоб выяснить «Время на выполнение заказа», необходимо «Число заготовок, передаваемых в работу» поделить на «Производительность».

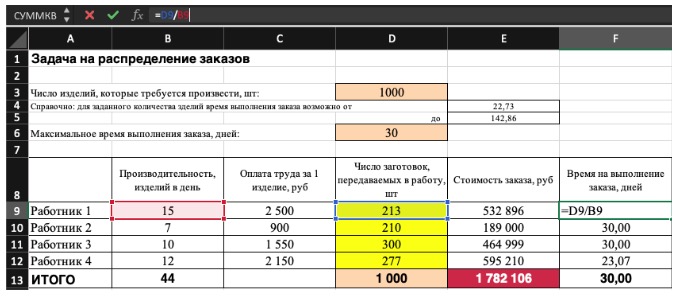
3) Выделите мотивированную ячейку, которая обязана показать максимум, минимум либо определенное значение при данных критериях. Для этого на панели нажмите «Данные» и выберете функцию «Поиск решений» (обычно она в верхнем правом углу).

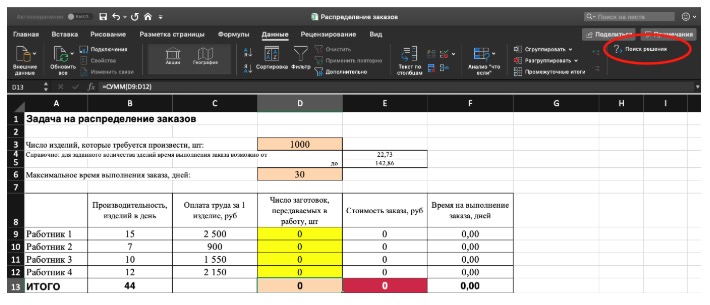
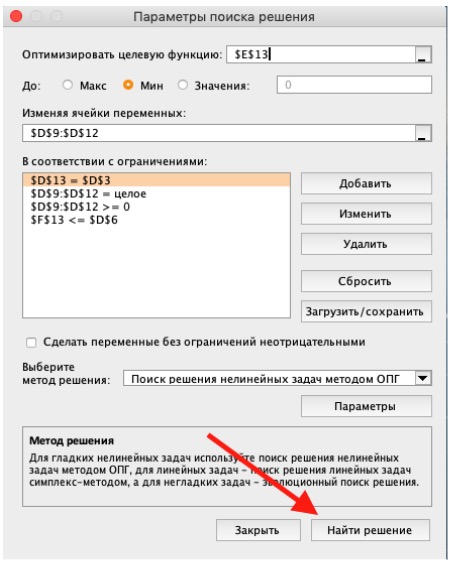
4) Заполните характеристики «Поиска решений» и нажмите «Отыскать решение».

Совокупная стоимость 1000 изделий рассчитывается как сумма стоимостей количества изделий от всякого работника. Данная ячейка (Е13) — это мотивированная функция. D9:D12 — изменяемые ячейки. «Поиск решений» описывает их рациональные значения, чтоб мотивированная функция достигнула минимума при данных ограничениях.

В нашем примере последующие ограничения:

• полное количество изделий 1000 штук ($D$13 = $D$3);
• число заготовок, передаваемых в работу — целое и больше нуля или равно нулю ($D$9:$D$12 = целое, $D$9:$D$12 > = 0);
• количество дней меньше или равно 30 ($F$9:$F$12 < = $D$6, или как в примере в ячейке F13 задать функцию МАКС(F9:F12) и поставить ограничение $F$13 < = $D$6).

5) В конце проверьте приобретенные данные на соответствие данному мотивированному значению. Если что-то не сходится — необходимо пересмотреть начальные данные, введенные формулы и ограничения.

Эта функция поможет улучшить работу и стремительно отыскать подходящий итог. На онлайн-курсе «Excel для карьеры и поиска работы» от Changellenge >> ToolKit мы делимся лишь теми функциями, которые вправду понадобятся на практике. Присоединяйтесь и начните работать отлично!

Получите карьерную поддержку

Если вы не понимаете, с что начать карьеру, зашли в тупик либо считаете, что сделали какие-то ошибки, спросите совета у профессионалов. Заполните заявку и консультанты Changellenge >> окажут для вас помощь. Это хороший шанс вкупе профессионалом проработать проблемные вопросцы и составить служебный план.

Подписаться на карьерную рассылку

Подписывайтесь на рассылку и получайте карьерные советы — от выбора промышленности и компании до лайфхаков по самоорганизации и развитию коммуникативных способностей.