Прогнозирование временных рядов в MS EXCEL (обзорная статья)

Прогнозирование временных рядов в MS EXCEL (обзорная статья)

В первом разделе статьи модели для прогнозирования временных рядов сравниваются с моделями, построение которых основано на причинно-следственных закономерностях.

Во 2-м разделе приведен лаконичный обзор трендов временных рядов (линейный и сезонный тренд, стационарный процесс). Для всякого тренда предложена модель для прогнозирования.
Потом даны ссылки на веб-сайты по теории прогнозирования временных рядов и содержащие базы статистических данных.

Disclaimer:
Напоминаем, что задачка веб-сайта excel2.ru (раздел Временные ряды ) показать внедрение MS EXCEL для решения задач, связанных с прогнозированием временных рядов. Потому, статистические определения и определения приводятся только для логики изложения и демонстрации мыслях. Веб-сайт не претендует на математическую строгость изложения статистики. Но в наших статьях:
• ПОЛНОСТЬЮ описан интегрированный в EXCEL инструментарий по анализу временных рядов (в составе надстройки Пакет анализа , разных типов Диаграмм ( гистограмма , линия тренда ) и формул);
• сделаны файлы примера для построения соответственных графиков, прогнозов и их интервалов пророчества, вычисления ошибок, генерации рядов (с трендами и сезонностью ) и пр.

Модели временных рядов и модели предметной области

Напомним, что временным рядом (англ. Time Series) именуют совокупа наблюдений изучаемой величины, упорядоченную по времени. Наблюдения выполняются через схожие периоды времени. Иной информацией, не считая наблюдений, исследователь не владеет.

Главный целью исследования временного ряда является его прогнозирование – пророчество будущих значений изучаемой величины. Прогнозирование основывается лишь на анализе значений ряда в прошлые периоды, поточнее — на идентификации трендов ряда. Потом, опосля определения трендов, делается моделирование этих трендов и, в конце концов, при помощи этих моделей — экстраполяция на будущие периоды.

Таковым образом, прогнозирование основывается на фактических данных (значениях временного ряда) и модели ( скользящее среднее , экспоненциальное выравнивание , двойное и тройное экспоненциальное выравнивание и др.).

Примечание : Прогнозирование способом Скользящее среднее в MS EXCEL тщательно рассмотрено в одноименной статье .

В отличие от способов временных рядов, где зависимости ищутся снутри самого процесса , в «моделях предметной области» (англ. «Causal Models») не считая самих данных употребляют к тому же законы предметной области.

Примером построения «моделей предметной области» ( моделей строящихся на базе причинно-следственных закономерностей, априорно узнаваемых независимо от имеющихся данных ) быть может промышленный процесс производства защитной ткани (Строение тканей живых организмов изучает наука гистология). Пусть в таком процессе понятно, что крепкость материала ткани (Строение тканей живых организмов изучает наука гистология) зависит от температуры в реакторе, в котором делается процесс полимеризации (температура — управляемый фактор). Но, крепкость материала является все таки случайной величиной, т.к. зависит кроме температуры также и от огромного количества остальных причин (свойства начального сырья, температуры окружающей среды, номера смены, умений аппаратчика реактора и пр.). Эти остальные причины в процессе производства стараются держать неизменными (сырье проходит входной контроль и его поставщик не изменяется; в помещении, где стоит реактор, поддерживается неизменная температура в течение всего года; аппаратчики проходят обучение (педагогический процесс, в результате которого учащиеся под руководством учителя овладевают знаниями, умениями и навыками) и часто проводится переаттестация). Задачей статистических способов в этом случае – предсказать значение случайной величины (прочности) при данном значении изменяемого фактора (температуры).

Обычно для описания таковых действий (зависимость случайной величины от управляемого фактора) являются предметом исследования в разделе статистики « Регрессионный анализ », т.к. есть основания создать догадку о существовании причинно-следственной связи меж управляемым фактором и предсказуемой величиной.

Модели, строящиеся на базе причинно-следственных закономерностей, упомянуты в данной статье для того чтоб акцентировать, что их исследование предшествует теме «временные ряды». Так, часть способов, к примеру «Регрессионный анализ» (употребляется способ меньших квадратов — МНК ), употребляется при анализе временных рядов, но изучаются в моделях предметной области, потому неподготовленным «любознательным мозгам» не стоит игнорировать раздел статистики « Статистический вывод », в котором проверяются догадки о равенстве среднего значения и строятся доверительные интервалы для оценки среднего , и упомянутый выше «Регрессионный анализ».

Коротко о типах действий и моделях для их прогнозирования

Выбор пригодной модели прогнозирования делается с учетом типа моделируемого процесса (наличие трендов). Разглядим главные типы действий.

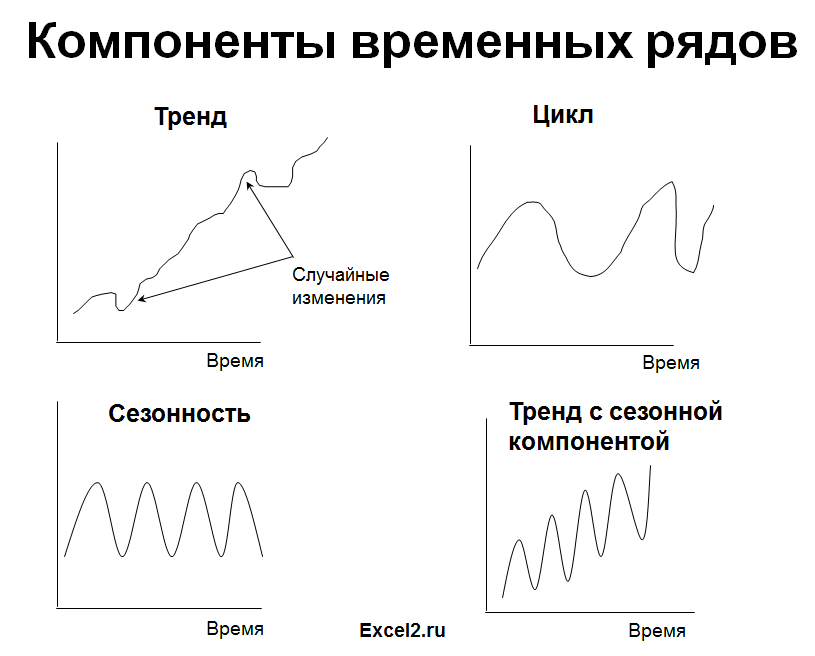
1. Стационарный процесс

Стационарный процесс – это случайный процесс чьи свойства не зависят от времени их наблюдения. Этими чертами являются среднее значение , дисперсия и автоковариация. В стационарном процессе не могут быть выделены прогнозируемые паттерны. Соответственно ряды демонстрирующие тренд и сезонность — не стационарны. А вот ряд с цикличностью (апериодической) является стационарным, т.к. на длительном временном интервале возникновение циклов предсказать нереально.

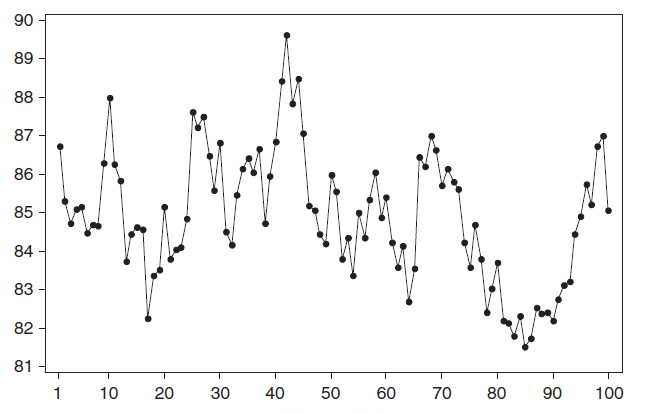
Почему стационарный процесс важен? Потому что стационарность предполагает нахождение процесса в состоянии статистической стабильности, то такие временные ряды имеют неизменное среднее значение и дисперсию, которые определяются обычным образом.

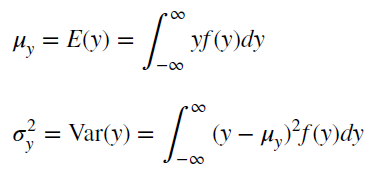
Также для стационарного процесса определяется функция автокорреляции – совокупа коэффициентов корреляции значений временного ряда с своими значениями, сдвинутыми по времени на один либо несколько периодов. Сдвиг на несколько временных периодов нередко именуется лагом (обозначается k).

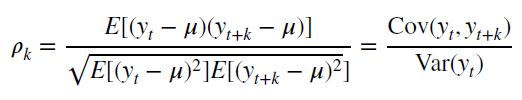
Функция автокорреляции является принципиальным источником инфы о временном ряде.

Примером стационарного процесса является колебания биржевого индекса, состоящего из цены акций нескольких компаний, около определённого значения (в период стабильности рынка).

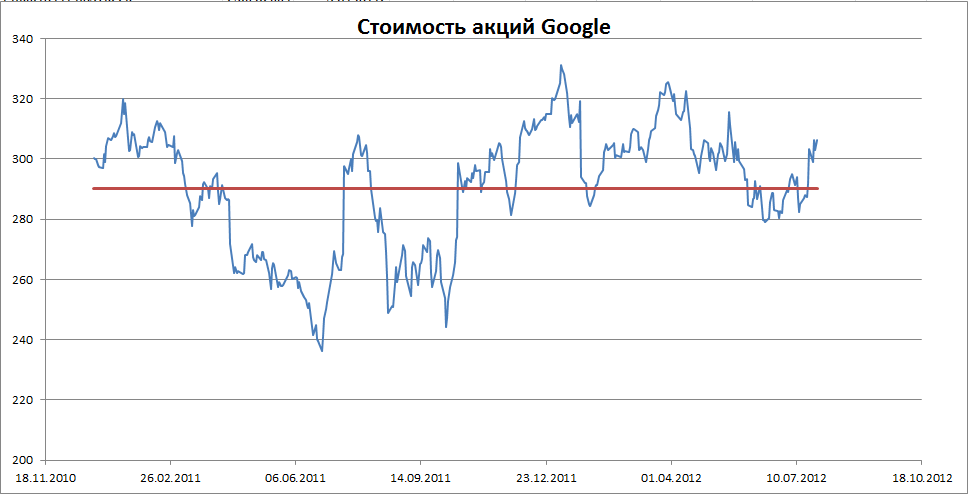
Примечание : график цены акций построен на настоящих данных, см. файл примера Гугл .

Особым видом стационарного процесса является белоснежный шум. У этого процесса: среднее значений ряда равно 0, имеется конечная дисперсия и отсутствует корреляция меж значениями начального ряда и рядом сдвинутым на случайное количество периодов (лагов). В MS EXCEL белоснежный шум можно сгенерировать функцией СЛЧИС().

2. Линейный тренд

Некие процессы генерируют тренд (однообразное изменение значений ряда). К примеру, линейный тренд y=a*x+b, поточнее y=a*t+b, где t – это время. Примером такового (не стационарного) процесса быть может однообразный рост цены недвижимости в неком районе.

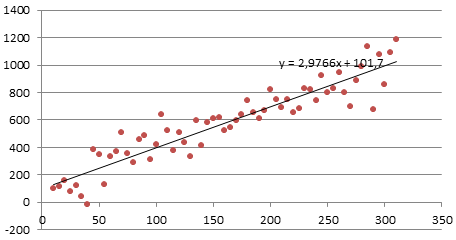
Для вычисления прогнозного значения можно пользоваться способами Регрессионного анализа и подобрать характеристики тренда: наклон и смещение по вертикали.

Примечание : Про генерацию случайных значений, демонстрирующих линейный тренд, можно поглядеть в статье Генерация данных для обычной линейной регрессии в EXCEL .

3. Процессы, демонстрирующие сезонность

В сезонном процессе находится буквально либо приблизительно фиксированный интервал конфигураций, к примеру, реализации неких продуктов имеют верно выраженный пик в ноябре-декабре всякого года в связи с праздничком.

Для прогнозирования рассчитывается индекс сезонности, потом ряд очищается от сезонной составляющие. Если ряд также показывает тренд, то опосля чистки от сезонности употребляются способы регрессионного анализа для вычисления тренда.

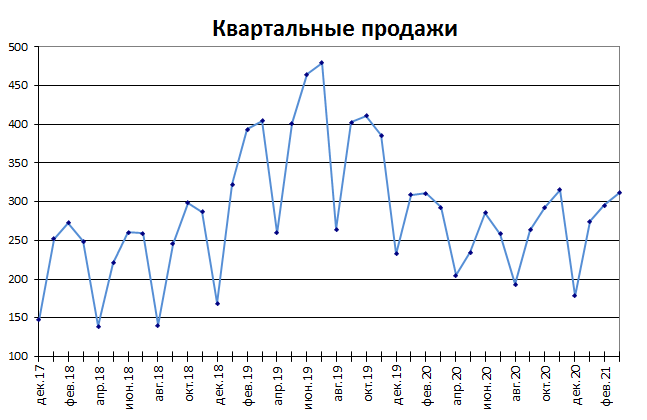
Примечание : Про генерацию случайных значений, демонстрирующих сезонность, можно поглядеть в статье Генерация сезонных трендов в EXCEL.

Нередко на практике встречаются ряды, являющиеся композицией вышеуказанных типов тенденций.

О моделях прогнозирования

В качестве простейшей модели для прогноза можно взять крайнее значение индекса. Данной модели соответствует последующий ход мысли исследователя: «Если значение индекса вчера было 306, то и завтра будет 306».

Данной модели соответствует формула Y _{прогноз(t)} = Y _t-1 (прогноз в момент времени t равен значению временного ряда в момент t-1).

Иной моделью является среднее за крайние несколько периодов ( скользящее среднее ). Данной модели соответствует иной ход мысли исследователя: «Если среднее значение индекса за крайние n периодов было 540, то и завтра будет 540». Данной модели соответствует формула Y _{прогноз(t)} =(Y _t-1 + Y _t-2 +…+Y _t-n )/n

Направьте внимание, что значения временного ряда берутся с схожим весом 1/n, другими словами наиболее ранешние значения (в момент t-n) влияют на прогноз также как и недавнешние (в момент t-1). Естественно, в случае, если идет речь о стационарном процессе (без тренда), таковая модель быть может применима. Чем больше количество периодов усреднения (n), тем меньше воздействие всякого личного наблюдения.

Третьей моделью для стационарного процесса быть может экспоненциальное выравнивание . В этом случае веса наиболее ранешних периодов будут меньше чем веса поздних. При всем этом учитываются все прошлые наблюдения. Вес всякого следующего наблюдения больше на 1-α (Фактор затухания), где α (альфа) – это константа выравнивания (от 0 до 1).
Данной модели соответствует формула Y _{прогноз(t)} =α*Y _t-1 + α*(1-α)*Y _t-2 + α*(1-α)2*Y _t-3 +…)

Формулу можно переписать через предшествующий прогноз Y _{прогноз(t)} =α*Y _t-1 +(1- α)* Y _{прогноз(t-1)} = α*(Y _t-1 — Y _{прогноз(t-1)} )+Y _{прогноз(t-1)} = α*(ошибка прошедшего прогноза)+ прошедший прогноз

При экспоненциальном выравнивании прогнозное значение равно сумме крайнего наблюдения с весом альфа и предшествующего прогноза с весом (1-альфа). Данной модели соответствует последующий ход мысли исследователя: «Вчера рано днем я предвещал, что индекс будет равен 500, но вчера в конце денька значение индекса составило 480 (ошибка составила 20). Потому за базу нынешнего прогноза я беру вчерашний прогноз и изменяю его на величину ошибки, умноженную на альфа. Параметр альфа (константа) я найду способом экспоненциального выравнивания».

Подробнее о способе прогнозирования на базе экспоненциального выравнивания можно отыскать в данной статье .

Нужный сигнал и шум

Из-за случайного разброса, присущему временному ряду, временной ряд представляют как комбинацию 2-ух разных компонент: полезного сигнала и шума (ошибки). Нужный сигнал следует одному из 3-х вышеуказанных типов действий. Сигнал быть может смоделирован и соответственно спрогнозирован. Шум представляет собой случайные ошибки (со средним значением =0, отсутствием корреляции и с фиксированной дисперсией ).

Главный задачей моделирования идентификация полезного сигнала, имеющего определенный тренд, от непредсказуемого шума. Для этого как раз и употребляются Модели выравнивания.

Способы и формулы прогнозирования в Excel

В этом руководстве рассматриваются простые способы прогнозирования, которые можно применить в таблицах Microsoft Excel. Это управление создано для менеджеров и управляющих, которым принципиально предугадать спрос потребителей. Теория иллюстрирована на базе Microsoft Excel. Наиболее подробные аннотации доступны для разрабов, которые желали бы воспроизвести теорию в приспособленном приложении.

Достоинства прогнозирования

Прогнозирование поможет для вас принимать правильные решения и зарабатывать/сберегать средства. Ниже приведен пример

• Выбирайте лучший размер товарных припасов

Как? Методом прогнозирования!

Как упростить задачку: обозначения, комменты, названия файлов

Со временем по мере скопления данных, у вас будет больше шансов запутаться и совершать ошибки. Есть ли решение? Будьте организованными: правильное внедрение обозначений, объяснений и присвоение понятных имен файлам сбережет много времени.

• Постоянно давайте обозначение столбцам. В первой строке всякого столбца постоянно давайте описание содержащихся в этом столбце данных.
• Различные данные, различные столбцы. Не помещайте в один столбец разнородные данные (к примеру, издержки и размер продаж. Весьма возможно, что вы запутаетесь, и вычисления и работа с данными будут весьма усложнены.
• Давайте любому файлу понятное имя. Это не просит огромных усилий, зато существенно ускоряет работу. Правильные имена разрешают стремительно отыскать подходящий файл зрительно либо через программку поиска файлов в Windows.

• Используйте комменты.

The usefulness of comments

Их можно применять:

• для разъяснения содержимого ячейки (к примеру, стоимость единицы продукции по оценке Мистера Доу)
• чтоб бросить предупреждения будущим юзерам таблицы (к примеру, у меня есть сомнения по поводу этих вычислений. )

Начало: обычной пример прогнозирования с внедрением полосы тренда

Viewing your data

Давайте получим 1-ый прогноз. В данной части мы будем применять последующий файл: Example1.xls. Данные приведены в качестве примера.

Наши данные: В первом столбце содержатся данные о стоимости единицы похожих продуктов. Стоимость единицы продукта отражает свойство продукта. Во 2-м столбце — данные о объеме продаж.

Что мы желаем выяснить: Если мы будем продавать иной продукт, свойства соответственного стоимости в $150 за единицу, сколько предположительно единиц продукции мы продадим?

Каким образом мы можем это выяснить: Все достаточно просто. Нам необходимо отыскать обычное математическое соотношение меж ценой единицы продукта и объемом продаж, а потом применять это соотношение для построения прогноза.

Сначала, постоянно полезно выстроить в Excel график, чтоб узреть графическое представление данных. Ваши глаза являются красивым инструментов в определении тренда за несколько секунд.

Для этого, избираем наши данные, потом используем Вставка > Диаграмма, и изберите Точечную. Мы желаем представить график продаж в виде функции свойства, потому на горизонтальной оси разместим стоимость продукта, а размер продаж на вертикальной оси.

Сейчас остановимся на несколько секунд и отлично разглядим получившуюся диаграмму: соотношение кажется растущим и линейным.

Чтоб осознать четкое отношение меж данными, в меню «Диаграмма» выберем опцию «Добавить линию тренда».

Создание полосы тренда

Сейчас наша линия тренда отобразилась на диаграмме. Кликнув на диаграмме правой клавишей можно получить четкое уравнение зависимости: y = 102.4x — 191.64.

Осознаем: Количество проданных продуктов = 102.4 помножить на стоимость продукта — 191.64.

Потому, если мы решим создавать продукты по стоимости $150 за единицу, мы можем представить, что размер продаж составит: 102.4*150 — 191.64 = 15168 штук.

Тем не наименее, будьте аккуратны: программное обеспечение постоянно может выявить зависимость меж 2-мя столбцами, даже если в действительности эта зависимость весьма слабенькая! Как следует, необходимо протестировать надежность. Ах так это делается:

• Сначала, постоянно обращайте внимание на диаграмму. Если вы обнаружите, что точки размещены близко к полосы тренда, как в нашем примере, то велик шанс того, что зависимость надежна. Если же точки размещены достаточно беспорядочно и далековато от полосы тренда, тогда необходимо быть внимательными: корреляция слабенькая, и недозволено слепо доверять установленной зависимости.

Точки размещены беспорядочно: нет тривиальной зависимости, ненадежные прогнозы

Точки «понятны» и разрешают получить наиболее надежный прогноз

• Опосля оценки диаграммы, вы сможете применять функцию КОРРЕЛ. В нашем примере функция будет иметь вид: КОРРЕЛ(A2:A83,B2:B83). Если итог близок к 0, тогда корреляция слабенькая, и вывод такой: настоящего тренда просто не существует. Если значение близко к 1, тогда корреляция мощная. Крайнее весьма помогает, потому что это наращивает силу разъяснения выявленной вами закономерности.

Естественно, эти крайние шаги можно заавтоматизировать: для вас не надо записывать зависимость либо воспользоваться для вычислений карманным калькулятором. Для вас нужен Пакет аналитических инструментов!

Прогнозирование с внедрением Пакета аналитических инструментов

Перед тем, как продолжить, проверьте, что Excel ATP (Пакет аналитических инструментов) установлен. Для получения подробной инфы обратитесь к секции Установка Пакета аналитических документов.

К огорчению, такие безупречные данные с таковой обычной и ясной линейной зависимостью достаточно редки в настоящей жизни. Давайте взглянем, что дает Excel для наиболее сложных случаев с наиболее сложными данными.

Идем далее: пример экспоненциальной зависимости

Как вы сможете осознать, таковая линейная модель не постоянно подступает. Практически, есть много обстоятельств принять экспоненциальную модель. Огромное количество экономических моделей являются экспоненциальными зависимостями (традиционным примером является расчет сложных процентов).

Ниже изложено, как произвести подгонку под экспоненциальную модель:

1) Поглядите на свои данные. Нарисуйте обычной график и просто поглядите на него. Если он соответствует экспоненциальному развитию, он должен смотреться так:

Безупречная экспоненциальная форма

Потом, как обычно, получите уравнение полосы.

2) К счастью, все это можно сделать впрямую, используя Пакет аналитических инструментов: введите все свои данные в пустую таблицу Excel и в меню изберите Инструменты => Анализ данных

Установка Пакета аналитических инструментов

Это пакет является дополнением к Microsoft Excel, но он не постоянно установлен по дефлоту. Для его установки необходимо сделать последующее:

1. Удостоверьтесь, что у вас есть установочный диск Office. Excel может запросить вставить диск для установки файлов Пакета.
2. Откройте таблицу Excel и в меню Инструменты изберите Дополнения. Отметьте 1-ый пункт в окне под заглавием « Analysis ToolPack (Пакет аналитических инструментов) ».
3. Вставьте диск Office CD, если будет нужно.
4. Готово! Направьте внимание, что в меню « Инструменты » сейчас больше пт, в том числе функция « Анализ данных ». Это конкретно та, которой мы будем воспользоваться больше всего.

Внедрение Пакета аналитических инструментов

. в случае линейной функции

Давайте вернемся к нашему линейному примеру. Если ваши данные « смотрятся » отлично (см. иллюстрации выше), вы сможете пользоваться Пакетом для получения приближения впрямую из многофункциональной формы, без прохождения процесса « прибавления тренда ».

Откройте таблицу с данными, потом откройте меню «&nbspинструменты » и изберите « анализ данных ». Выйдет всплывающее окно с вопросцем какой вид анализа вы желаете провести. Для линейных функций изберите « регрессия ».

Сейчас необходимо отдать Excel два аргумента: « шкала Y » и « шкала X ». Шкала Y указывает, что вы желаете высчитать (к примеру, размер продаж), а на шкале X отражаются данные, которые, как вы думаете, разъясняют размер продаж (в нашем примере, стоимость единицы продукта). В нашем примере (см. example1.xls), данные о объеме спроса содержатся в столбце B, в строчках с 3 по 90, потому для шкалы Y для вас нужно указать « $B$3:$B$90 » и «$A$3:$A$90 » для шкалы X. Когда закончите, нажмите « ok ».

Итог Пакета аналитических инструментов в случае регрессии способа меньших квадратов

В данной таблице также содержится полезное значение, которое даст для вас представление о том, как точны ваши вычисления: « R Square ». Если это значение близко к 1, тогда ваши приближения довольно четкие, и это значит что приобретенное уравнение является довольно четким представлением ваших данных. Если это значение близко к 0, то приближение недостаточно не плохое, и, может быть, для вас необходимо испытать другую модель (см. дальше экспоненциальная модель).

Этот способ, может быть, резвее, чем техника « полосы тренда ». Тем не наименее, это в большей степени технический и наименее приятный процесс. Потому если вы не желаете строить графики на основании ваших данных и оценивать их, по последней мере, проверьте значение « R square ».

. используя экспоненциальную модель

Если линейная модель не подступает (если вы получили низкое значение R-square, к примеру 0,1), может быть, для вас нужно применять экспоненциальную модель.

Запустите Пакет инструментов, как обычно: Откройте таблицу, потом откройте меню « Инструменты » и изберите « Анализ данных ». Вы увидите всплывающее окно с вопросцем, какой вид анализа вы желаете провести. Для экспоненциальной модели, избираем « экспоненциальная ».

Направьте внимание, что Excel просит вас указать спектр входящих данных. Изберите столбец, в котором содержатся данные, в отношении которых вы желаете выстроить прогноз (к примеру, стоимость единицы продукта) и изберите “смягчающий фактор”.

Как выяснить, какую модель избрать?

Направьте внимание, что для вас не надо пробовать любой способ и потом выбирать, какой из их подступает идеальнее всего. Этого можно достигнуть методом автоматизации, потому что существует большущее количество доступных способов. Если вы желаете протестировать на собственных данных все модели, вы сможете выслать их в Lokad. У нас есть мощная it система которая “тестирует” все модели и выбирает лишь те, которые идеальнее всего работают с данными вашего бизнеса (наиболее подробная информация о продуктах Lokad).

Создание прогноза в Excel для Windows

Если у вас есть статистические данные с зависимостью от времени, вы сможете сделать прогноз на их базе. При всем этом в Excel создается новейший лист с таблицей, содержащей статистические и предсказанные значения, и диаграммой, на которой они отражены. При помощи прогноза вы сможете предвещать такие характеристики, как будущий размер продаж, потребность в складских припасах либо потребительские тенденции.

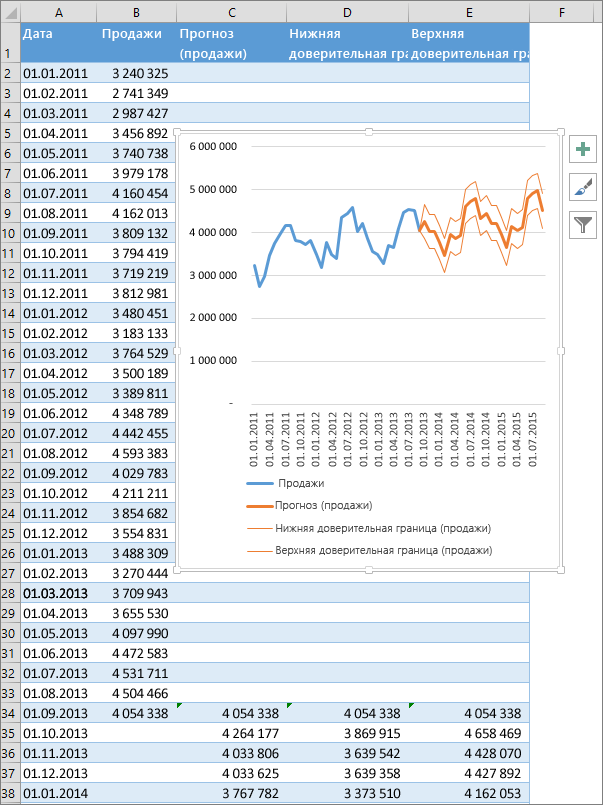
Создание прогноза

На листе введите два ряда данных, которые соответствуют друг дружке:

ряд значений даты либо времени для временной шкалы;

ряд соответственных значений показателя.

Эти значения будут предсказаны для дат в будущем.

Примечание: Для временной шкалы требуются схожие интервалы меж точками данных. К примеру, это могут быть месячные интервалы со значениями на 1-ое число всякого месяца, годовые либо числовые интервалы. Если на временной шкале не хватает до 30 % точек данных либо есть несколько чисел с одной и той же меткой времени, это нормально. Прогноз все равно будет четким. Но для увеличения точности прогноза лучше перед его созданием обобщить данные.

Выделите оба ряда данных.

Совет: Если выделить ячейку в одном из рядов, Excel автоматом выделит другие данные.

На вкладке Данные в группе Прогноз нажмите клавишу Лист прогноза.

В окне Создание прогноза изберите график либо гограмму для зрительного представления прогноза.

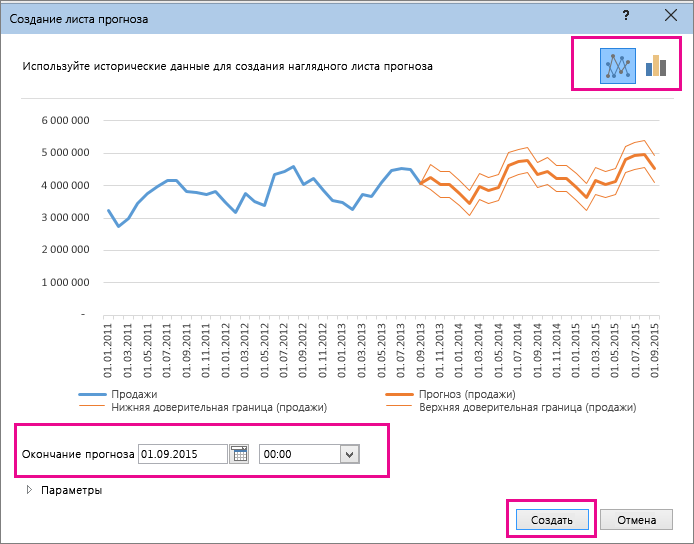
В поле Окончание прогноза изберите дату окончания, а потом нажмите клавишу Сделать.

В Excel будет сотворен новейший лист с таблицей, содержащей статистические и предсказанные значения, и диаграммой, на которой они отражены.

Этот лист будет находиться слева от листа, на котором вы ввели ряды данных (другими словами перед ним).

Настройка прогноза

Если вы желаете поменять доп характеристики прогноза, нажмите клавишу Характеристики.

Сведения о любом из вариантов можно отыскать в таблице ниже.

Характеристики прогноза

Начало прогноза

Изберите дату, с которой должен начинаться прогноз. При выбирании даты начала, которая наступает ранее, чем завершаются статистические данные, для построения прогноза употребляются лишь данные, предыдущие ей (это именуется «ретроспективным прогнозированием»).

Если вы начинаете прогноз перед крайней точкой, вы можете получить оценку точности прогноза, потому что можете сопоставить предсказуемый ряд с фактическими данными. Но если начать прогнозирование со очень ранешней даты, построенный прогноз может различаться от сделанного на базе всех статистических данных. При использовании всех статистических данных прогноз будет наиболее четким.

Если в ваших данных выслеживаются сезонные тенденции, то рекомендуется начинать прогнозирование с даты, предыдущей крайней точке статистических данных.

Доверительный интервал

Установите либо снимите флаг Доверительный интервал, чтоб показать либо скрыть его. Доверительный интервал — это спектр вокруг всякого предсказанного значения, в который в согласовании с прогнозом (при обычном распределении) предположительно должны попасть 95 % точек, относящихся к будущему. Доверительный интервал помогает найти точность прогноза. Чем он меньше, тем выше достоверность прогноза для данной точки. Доверительный интервал по дефлоту определяется для 95 % точек, но это значение можно поменять при помощи стрелок ввысь либо вниз.

Сезонность — это число для длины (количества точек) сезонного шаблона и автоматом находится. К примеру, в каждогоднем цикле продаж, любой из которых представляет месяц, сезонность составляет 12. Автоматическое обнаружение можно переопрепредидить, выбрав установить вручную и выбрав число.

Примечание: Если вы желаете задать сезонность вручную, не используйте значения, которые меньше 2-ух циклов статистических данных. При таковых значениях этого параметра приложению Excel не получится найти сезонные составляющие. Если же сезонные колебания недостаточно значительны и методу не удается их выявить, прогноз воспримет вид линейного тренда.

Спектр временной шкалы

Тут можно поменять спектр, применяемый для временной шкалы. Этот спектр должен соответствовать параметру Спектр значений.

Спектр значений

Тут можно поменять спектр, применяемый для рядов значений. Этот спектр должен совпадать со значением параметра Спектр временной шкалы.

Заполнить отсутствующие точки при помощи

Для обработки отсутствующих точек в Excel употребляется интерполяция, другими словами отсутствующие точки будут заполнены в качестве взвешенного среднего значения примыкающих точек, если отсутствует наименее 30 % точек. Чтоб нули в перечне не были пропущены, изберите в перечне пункт Нули.

Внедрение агрегатных дубликатов

Если данные содержат несколько значений с одной меткой времени, Excel находит их среднее. Чтоб применять иной способ вычисления, к примеру Медиана либоКоличество,изберите подходящий метод вычисления из перечня.

Включить статистические данные прогноза

Установите этот флаг, если желаете поместить на новеньком листе доп статистическую информацию о прогнозе. При всем этом добавляется таблица статистики, сделанная при помощи прогноза. Ets. Функция СТАТ и характеристики, такие как коэффициенты выравнивания («Альфа», «Бета», «Палитра») и метрики ошибок (MASE, SMAPE, MAE, RMSE).

Формулы, применяемые при прогнозировании

При использовании формулы для сотворения прогноза ворачиваются таблица со статистическими и предсказанными данными и диаграмма. Прогноз предвещает будущие значения на базе имеющихся данных, зависящих от времени, и метода экспоненциального выравнивания (ETS) версии AAA.

Таблицы могут содержать последующие столбцы, три из которых являются вычисляемыми:

столбец статистических значений времени (ваш ряд данных, содержащий значения времени);

столбец статистических значений (ряд данных, содержащий надлежащие значения);

столбец предсказуемых значений (вычисленных при помощи функции ПРЕДСКАЗ.ЕTS);

два столбца, представляющие доверительный интервал (вычисленные при помощи функции ПРЕДСКАЗ.ЕTS.ДОВИНТЕРВАЛ). Эти столбцы показываются лишь при проверке доверительный интервал в разделе Характеристики.

Скачка эталона книжки

Доп сведения

Вы постоянно сможете задать вопросец спецу Excel Tech Community либо попросить помощи в обществе Answers community.

Прогнозирование продаж в Excel с учетом сезонности

В прошлой статье мы уже разобрали, что такое временной ряд и функцию тренда. Сейчас подробнее разберемся с терминологией и остановимся на одной из моделей временного ряда.

Из что состоит временной ряд

Уровни временного ряда (Yt) представляют из себя сумму 2-ух компонент:

1. Регулярную составляющую
2. Случайную составляющую

В свою очередь постоянная составляющая состоит из:

1. Тренда
2. Сезонности
3. Повторяющейся составляющей

Но, в модели необязательно наличие всех этих компонент сходу.

Случайная компонента отражает воздействие случайных возмущений на модель, которые по отдельности имеют незначимое действие, но суммарно их воздействие чувствуется.

Другими словами, в общем случае временной ряд представляет из себя наличие 4 составляющих:

1. Тренд (Tt)
2. Сезонность (St)
3. Цикличность (Ct)
4. Случайные возмущения (Et)

Повторяющаяся компонента, по сопоставлению с сезонностью, имеет наиболее долгий эффект и изменяется от цикла к циклу. Потому, ее обычно объединяют с трендом.

Виды моделей временного ряда

Обычно, выделяют две модели временного ряда и третью — смешанную.

Аддитивная модель

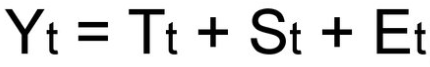
Мультипликативная модель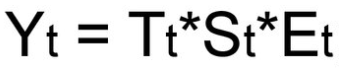

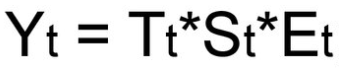
Смешанная модель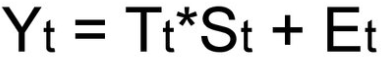

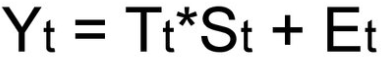
При выбирании нужной модели временного ряда глядят на амплитуду колебаний сезонной составляющей. Если ее колебания относительно постоянны, то выбирают аддитивную модель. Другими словами, амплитуда колебаний приблизительно схожа:

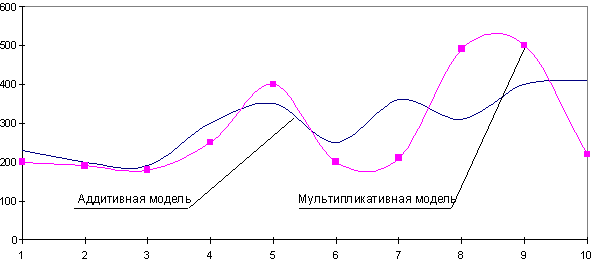
Если амплитуда сезонных колебаний увеличивается либо миниатюризируется, строят мультипликативную модель временного ряда, которая ставит уровни ряда в зависимость от значений сезонной составляющие.

Построение этих моделей сводится к расчету тренда (Tt), сезонности (St) и случайных возмущений (Et) для всякого уровня ряда (Yt).

Метод построения модели

1. Выравниваем ряд при помощи скользящей средней, другими словами сглаживаем ряд и отфильтровываем высокочастотные колебания.
2. Рассчитываем значение сезонной составляющие St.
3. Рассчитываем значения Tt с внедрением приобретенного уравнения тренда.
4. Используя приобретенные значения St и Tt, находим прогнозные значения уровней временного ряда.
5. Оцениваем свойство модели.

Реализация на практике

Итак, мы имеем на руках данные о продажах за 2016 и 2017 год и желаем спрогнозировать реализации на 2018 год.

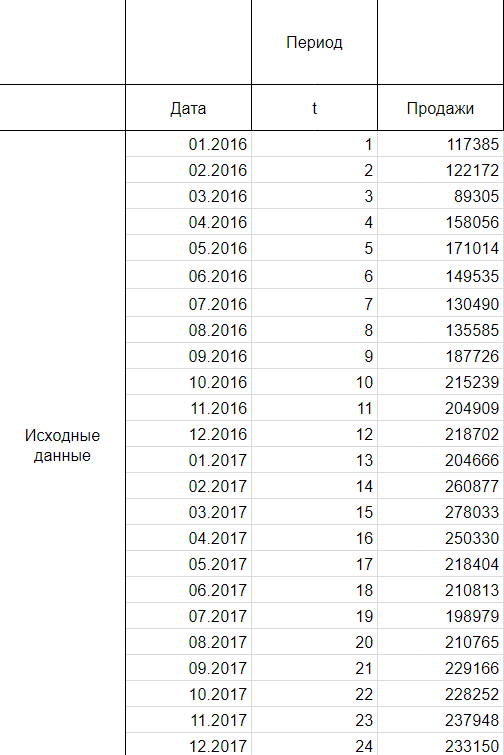
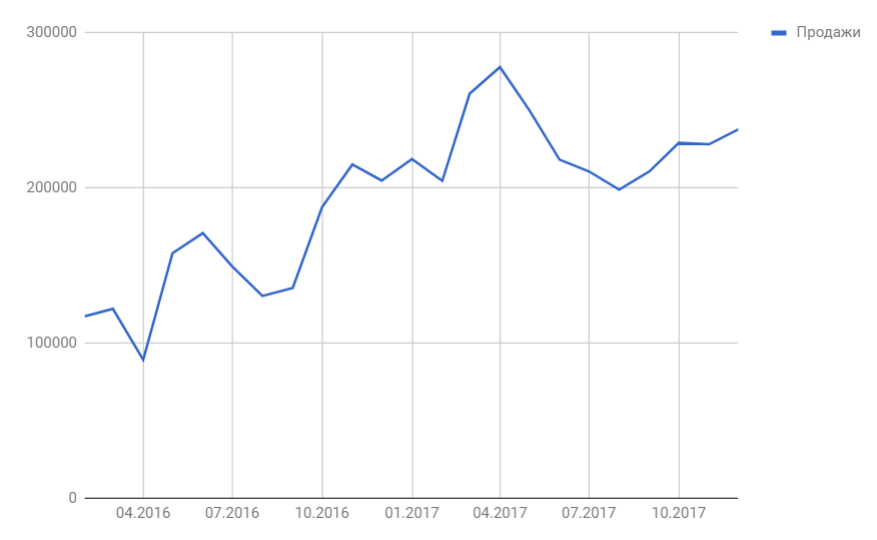
Шаг 1

Следуя нашему методу, мы должны сгладить временной ряд. Воспользуемся способом скользящей средней. Лицезреем, что в любом году есть огромные пики (май-июнь 2016 и апрель 2017), потому возьмем период выравнивания пошире, к примеру, месячную динамику, т.е. 12 месяцев.

Удобнее брать период выравнивания в виде нечетного числа, тогда формула для расчета уровней сглаженного ряда:

yi — фактическое значение i-го уровня ряда,

yt — значение скользящей средней в момент времени t,

2p+1 — длина интервала выравнивания.

Но потому что мы решили применять месячную динамику в виде четного числа 12, то данная формула нам не подойдет и мы воспользуемся данной:

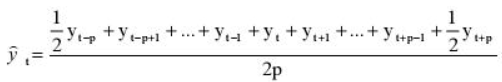
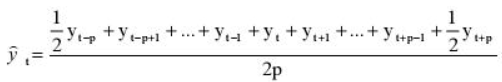
Другими словами, мы учитываем половины от последних уровней ряда в спектре, в остальном формула не перетерпела больше никаких конфигураций. Вот ее четкий вид для нашей задачки:

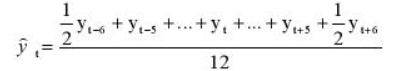
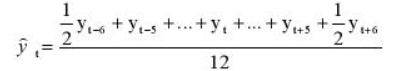
Сглаживаем наши уровни ряда и растягиваем формулу вниз:

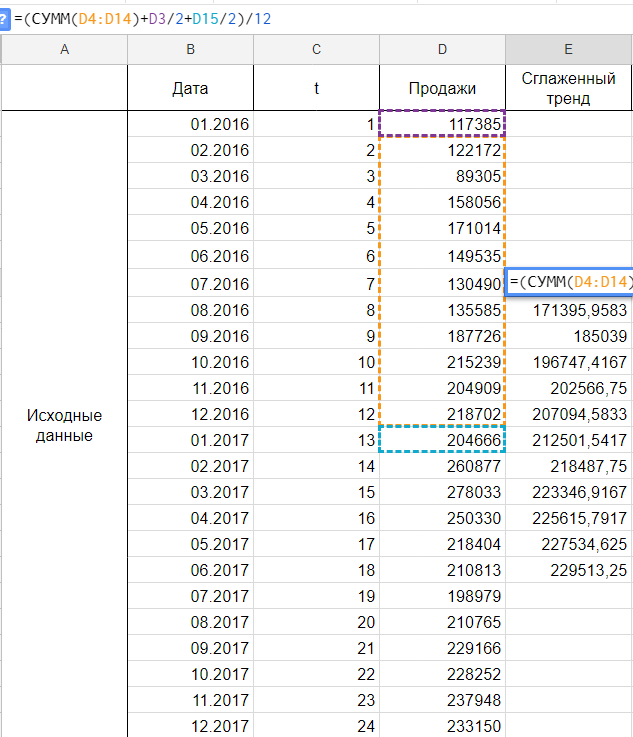
Сходу можем выстроить график из узнаваемых значений уровня продаж и их сглаженной. Выведем ее уравнение и значение коэффициента детерминации R^2:

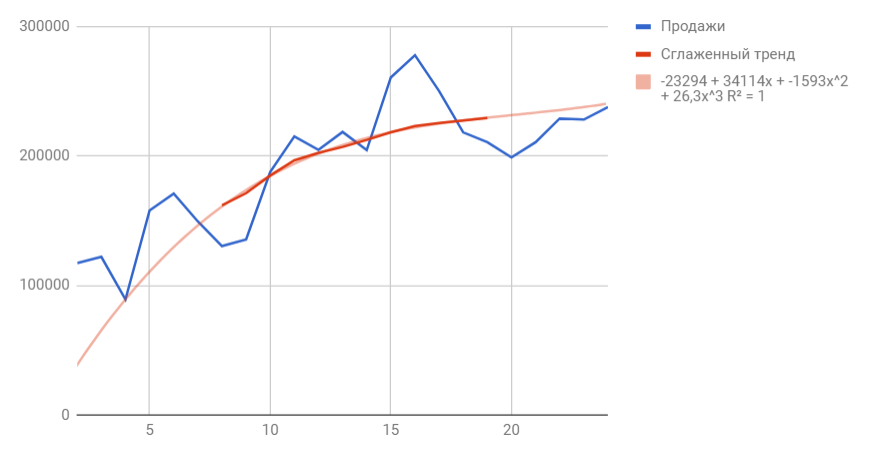
В качестве сглаженной я избрала полином третьей степени, потому что он идеальнее всего описывал уровни временного ряда и имел больший R^2.

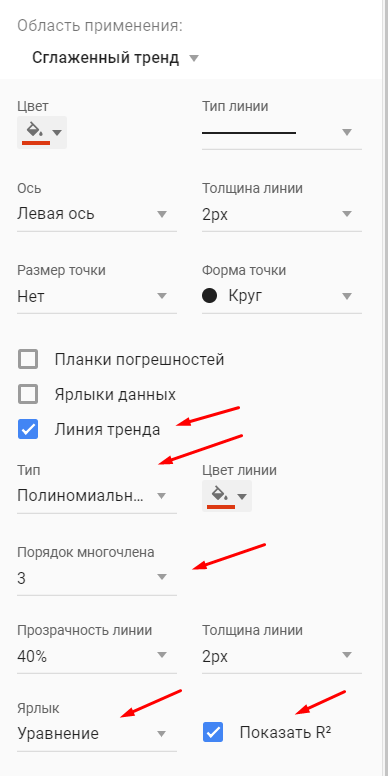
Шаг 2

Потому что мы рассматриваем аддитивную модель вида: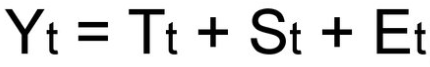

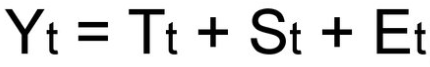
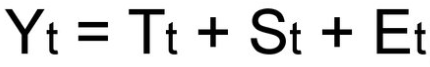
Найдем оценки сезонной составляющие как разность меж фактическими уровнями ряда и значениями скользящей средней St+Et = Yt-Tt, потому что Yt и Tt мы уже знаем.

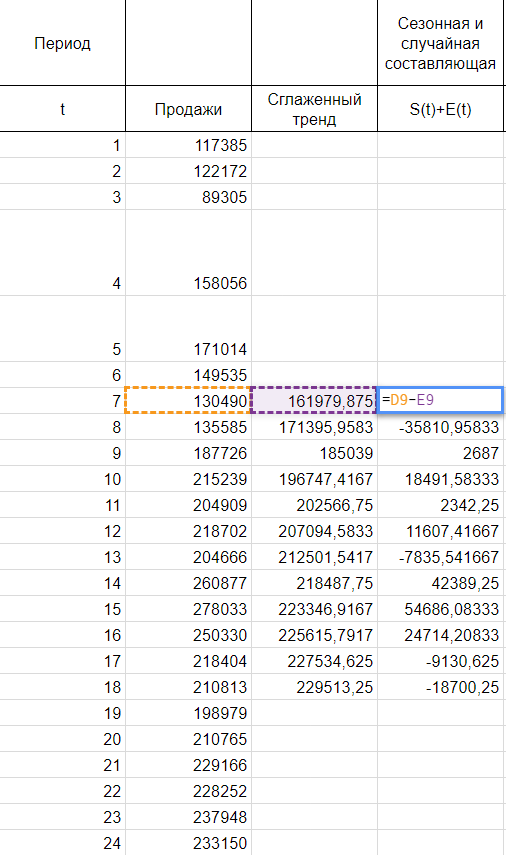
Используем оценки сезонной составляющие (St+Et) для расчета значений сезонной составляющие St. Для этого найдем средние за любой интервал (по всем годам) оценки сезонной составляющие St.

Средняя оценка сезонной составляющие находится как сумма по столбцу, деленная на количество заполненных строк в этом столбце. В нашем случае оценки сезонной составляющей расположились в строчках без пересечений, потому сумма по столбцам состоит из одиночных значений, как следует и среднее будет таковым же. Если б мы располагали периодом побольше, к примеру с 2015, у нас бы добавилась еще одна строчка и мы смогли бы всеполноценно отыскать среднее, поделив сумму на 2.

В моделях с сезонной компонентой обычно предполагается, что сезонные действия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной составляющие по всем интервалам обязана быть равна нулю. Потому обнаружив значение случайной составляющей, поделив сумму средних оценок сезонной составляющей на 12, мы вычитаем ее значение из каждой средней оценки и получаем скорректированную сезонную компоненту, St.

Дальше, заполняем нашу таблицу значениями сезонной составляющей дублируя ряд любые 12 месяцев, другими словами трижды:

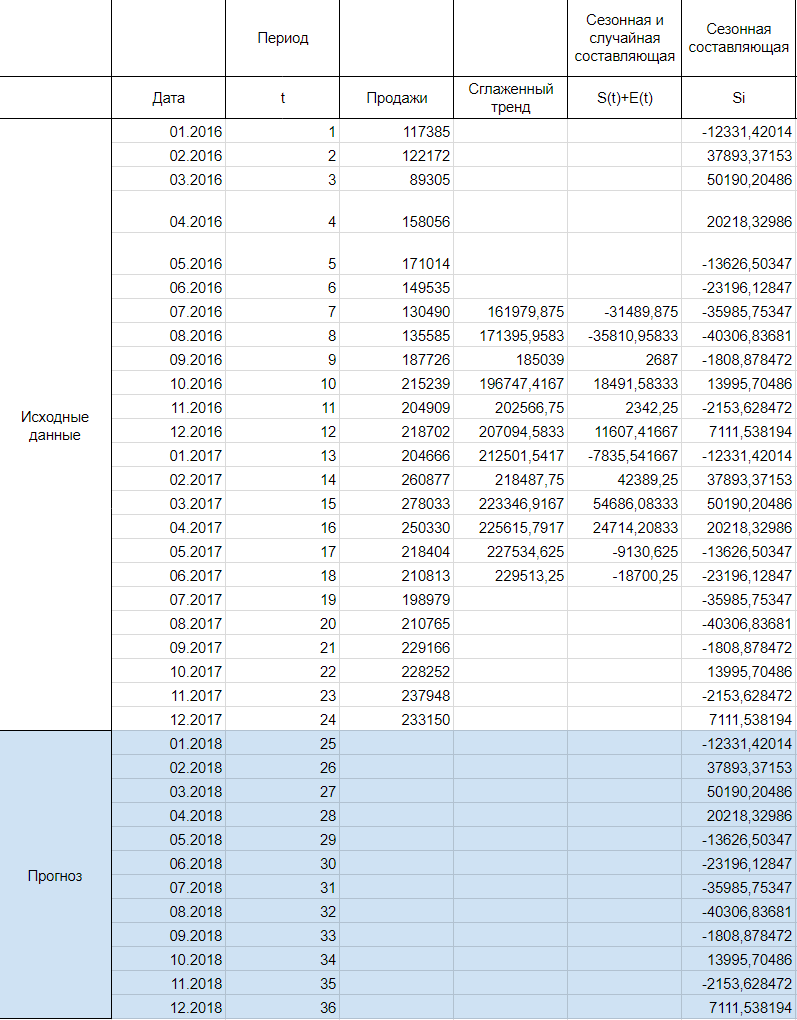
Шаг 3

Сейчас рассчитываем значения уровня тренда T(t) по тому уравнению, которое мы получили при построении сглаженного тренда на первом шаге.

T(t) = — 23294 + 34114 * t — 1593 *t^2 + 26,3 *t^3

Заместо t используем значения из столбца Период из соответственной строчки.

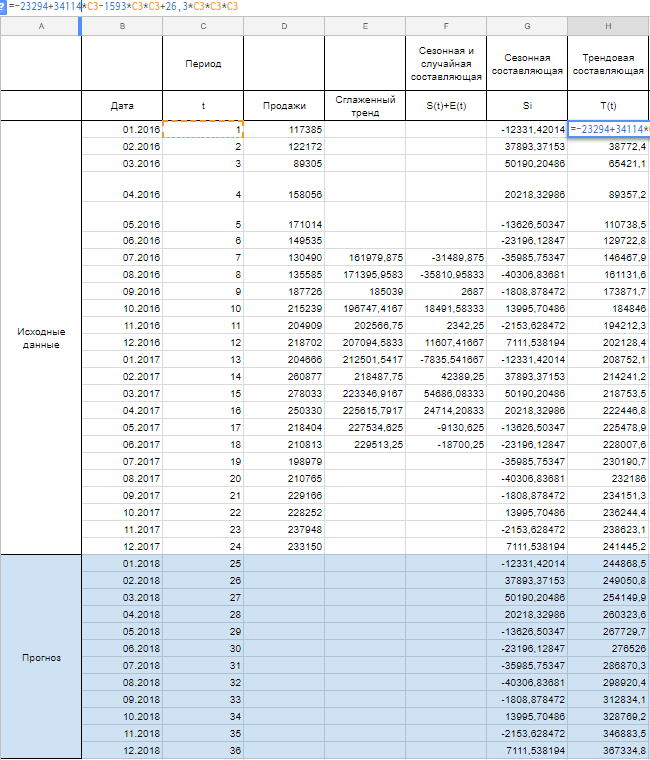
Шаг 4

Имея рассчитанные значения S(t) и T(t) мы можем высчитать прогнозные значения уровней ряда Y(t). Для этого накладываем уровни сезонности на тренд.

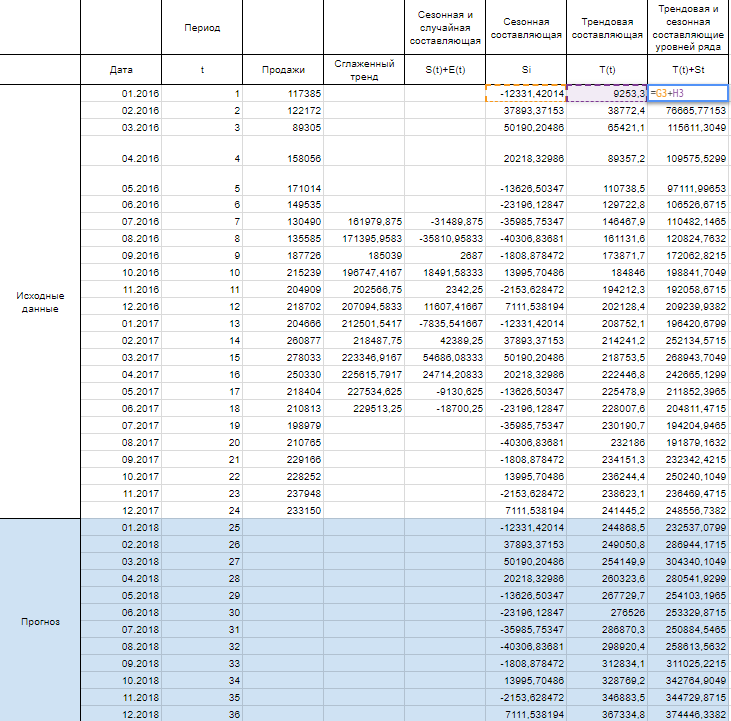
Сейчас построим график узнаваемых значений Y(t) и спрогнозированных за 2018 год.

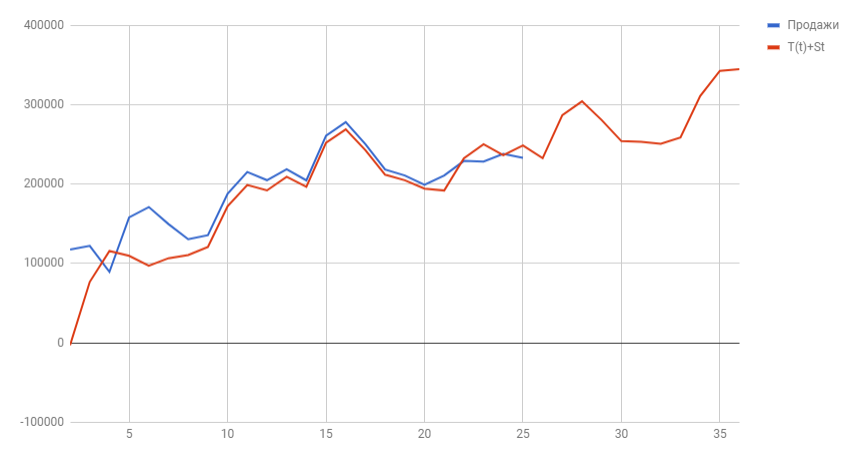
Вот мы и отыскали спрогнозированные значения уровней продаж на 2018 год. Значения отражают вырастающую тенденцию и сезонные пики. Естественно, эти данные не дают 100% точности, ведь существует огромное количество наружных действий, которые могут поменять направление тренда, потому к прогнозным значениям обычно строят доверительный интервал, это таковой коридор, снутри которого могут колебаться прогнозные значения с данной вероятностью (почаще всего выбирают 95%). Но о этом я расскажу в последующей статье.

Шаг 5

Осталось оценить точность модели. Для этого будем применять среднюю ошибку аппроксимации, которая поможет высчитать ошибку в относительном выражении. Другими словами, это среднее отклонение расчетных значений от фактических, которое рассчитывается по формуле:

yi — спрогнозированные уровни ряда,

yi* — фактические уровни ряда,

n — количество складываемых частей.

Модель может считаться адекватной, если:

Итак, рассчитываем ошибку аппроксимации для нашего варианта. Потому что в базе нашего тренда лежит полином третьей степени, прогнозные значения начинают отлично повторять фактические значения к концу 2016 года, думаю, я думаю, потому корректнее было бы высчитать ошибку аппроксимации для значений 2017 года.

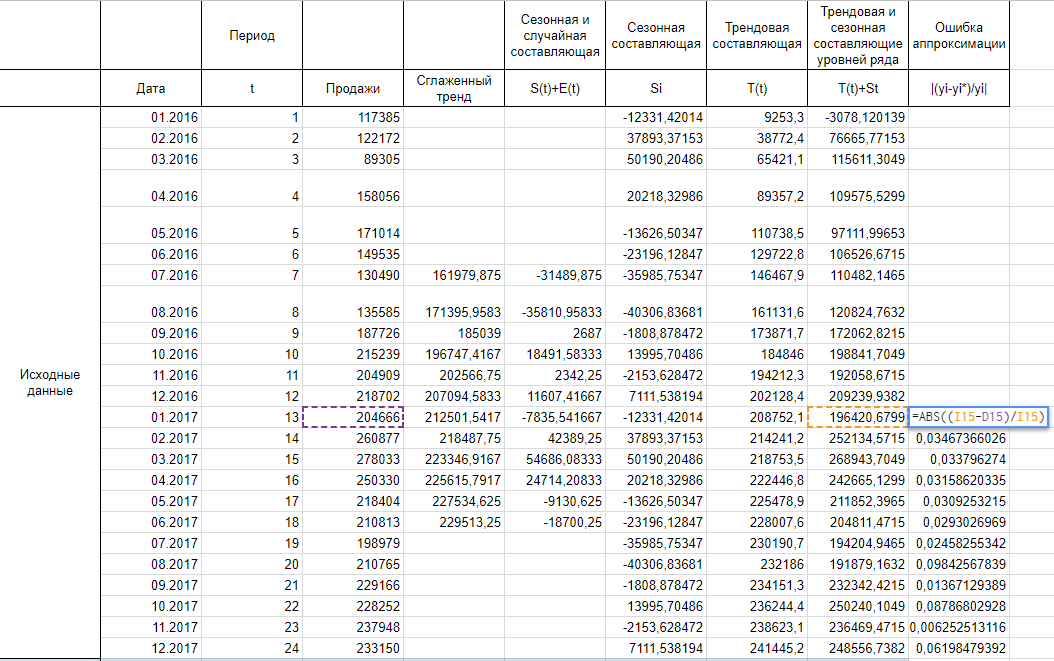
Сложив весь столбец с ошибками аппроксимации и поделив на 12, получаем среднюю ошибку аппроксимации 4,13%. Это значение меньше 15% и можем прийти к выводу о адекватности модели.

Не запамятовывайте, что прогнозы не бывают точными на 100%. Любые нежданные наружные действия могут развернуть значения уровней ряда в неведомом направлении 🙂