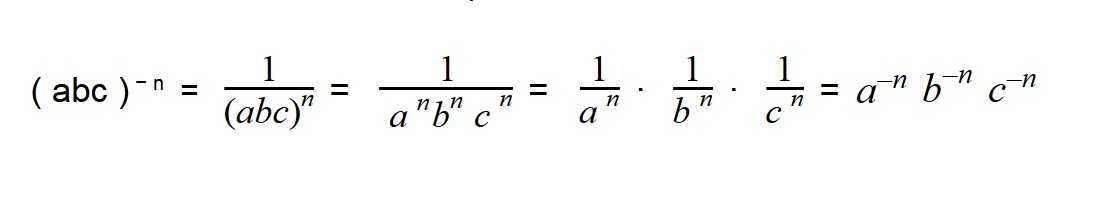Отрицательная степень

В учебниках по арифметике можно повстречать такое определение:

«Степенью n числа а является произведение множителей величиной а n раз попорядку»

К примеру, a n — степень, где:

• a — основание степени,
• n — показатель степени.

Читается такое выражение как a в степени n.

Если гласить проще, то степень, а поточнее показатель степени (n), гласит нам о том, сколько раз следует помножить данное число (основание степени) само на себя.

А означает, если у нас есть задача, где спрашивают, как возвести число в степень, к примеру, число 2 в третью степень, то она решается достаточно просто:

2 3 = 2 · 2 · 2, где:

• 2 — основание степени,
• 3 — показатель степени.

Таблица степеней

Тут мы приведем результаты возведения в степень натуральных чисел от 1 до 10 в квадрат (показатель степени два) и куб (показатель степени 3).

Характеристики степеней

Степень с натуральным показателем в арифметике имеет несколько принципиальных параметров, которые разрешают упрощать вычисления. Всего их 5 штук — ниже мы их разглядим.

Свойство 1: произведение степеней

При умножении степеней с схожими основаниями, основание мы оставляем без конфигураций, а характеристики степеней складываем:

a m · a n = a m + n

• a — основание степени.
• m, n — характеристики степени, любые натуральные числа.

Свойство 2: личное степеней

Когда мы делим степени с схожими основаниями, то основание остается без конфигураций, а из показателя степени делимого вычитают показатель степени делителя.

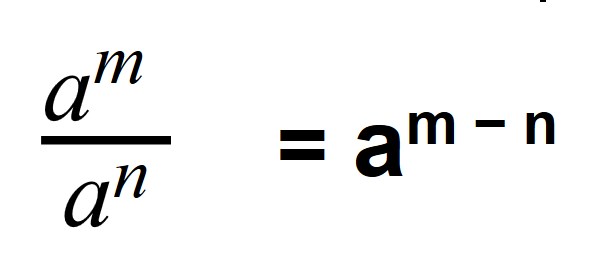
• a — хоть какое число, не равное нулю.
• m, n — любые натуральные числа, такие, что m > n

Свойство 3: возведение степени в квадрат

Когда возводим степень в степень, то основание степени остается неизмененным, а характеристики степеней множатся друг на друга.

• a — основание степени (не равное нулю).
• m, n — характеристики степени, натуральное число.

Свойство 4: степень произведения

При возведении в степень произведения любой из множителей возводится в степень. Потом приобретенные результаты перемножаются.

(a · b) n = a n · b n

• a, b — основание степени (не равное нулю).
• n — характеристики степени, натуральное число.

Свойство 5: степень личного

Чтоб возвести в степень личное, можно возвести в эту степень поначалу делимое, позже делитель, и 1-ый итог поделить на 2-ой.

(a : b) n = a n : b n

• a, b — основание степени (не равное нулю), любые оптимальные числа, b ≠ 0.
• n — показатель степени, натуральное число.

Степень с показателем 0

Хоть какое целое a ≠ 0 в степени 0 равно 1.

Выражение 0 в степени 0 почти все арифметики считают лишенным смысла, так график функции f (x, у) = xy прерывается в точке (0; 0).

Степень с отрицательным показателем

Число в минусовой степени равно дроби, числителем которой является единица, а знаменателем данное число с положительным показателем:

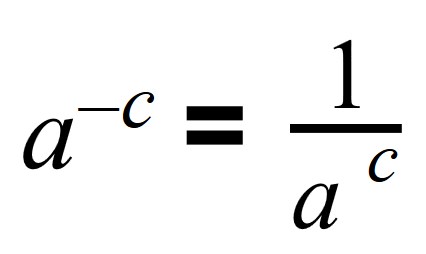
Например, 4 в минус 2 степени — это 1/4 2 , 2 в минус 3 степени — это 1/2 3 , 3 в минус 1 степени — это 1/3, 10 в минус первой степени — это 1/10 либо 0,1.

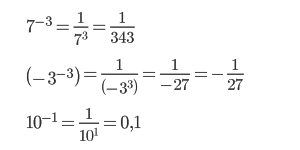
Степени с отрицательным показателям помогают компактно записывать очень малые либо повсевременно уменьшающиеся величины. К примеру, одну миллиардную долю (0, 000 000 001) можно записать как 10 в минус 9 степени (10 -9 ). В школьной программке такие величины — уникальность: почаще всего употребляют 10 в минус 1 степени либо 2 в минус 1 степени.

Чтоб разобраться, как возводить число в отрицательную степень, вспомним правило деления степеней с схожими основаниями.

Деление степеней с схожими основаниями, но различными показателями осуществляется по последующей формуле: характеристики отнимаются, а основание остается постоянным.

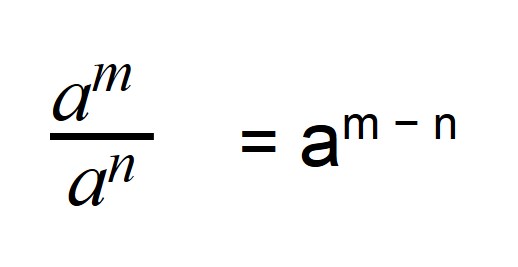
Потому если степень делимого будет меньше степени делителя, то в итоге получится число с отрицательной степенью:

a 3 : a 6 =a 3 — 6 = a -3

Если записать деление в виде дроби, то при сокращении в числителе остается 1, а в знаменателе число будет иметь положительную степень:

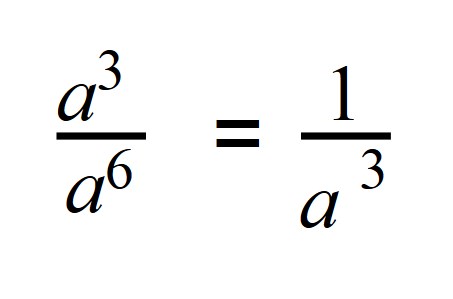
Деяния с отрицательными степенями

Умножение отрицательных степеней

При умножении отрицательных степеней с схожими основаниями характеристики степеней складываются, так же как и при умножении положительных степеней:

a m · a n = a m + n

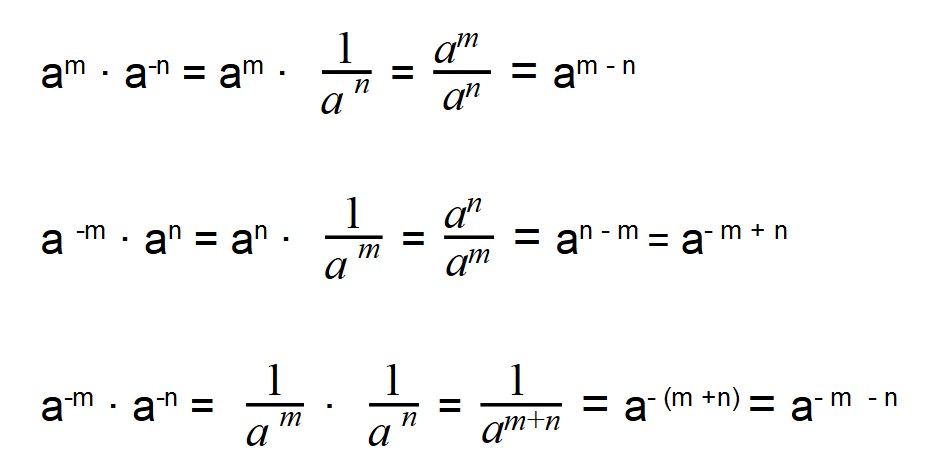
Деление отрицательных степеней

При делении отрицательных степеней с схожими основаниями из показателя степени делимого вычитается показатель делителя, так же как и при делении положительных степеней:



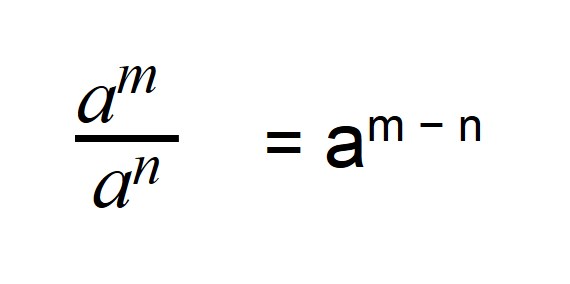
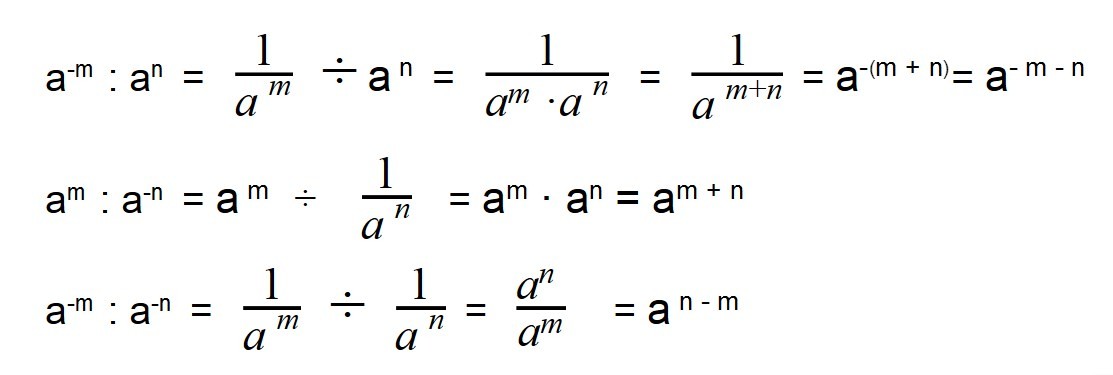
Возведение дроби в отрицательную степень

Чтоб возвести дробь в отрицательную степень, нужно возвести в эту степень раздельно числитель и знаменатель:

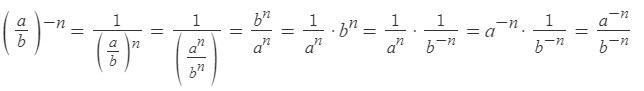
Возведение произведения в отрицательную степень

Чтоб возвести произведение в отрицательную степень, нужно возвести в эту степень любой множитель произведения раздельно: