Книжка «Традиционные задачки Computer Science на языке Java»

Привет, Хаброжители! Cтолкнулись с «неразрешимой» неувязкой при разработке программного обеспечения? Быстрее всего, кто-то уже совладал с данной нам задачей, и вы сможете не разламывать голову. Дэвид Копец собрал более полезные готовые решения, принципы и методы. «Традиционные задачки Computer Science на языке Java» — это мастер-класс по программированию, содержащий 55 практических примеров, затрагивающих самые животрепещущие темы: базисные методы, ограничения, искусственный ум и почти все другое.

— Рекурсия, мемоизация и битовые манипуляции.
— Поисковые, графовые и генетические методы.
— Задачи ограничений.
— Кластеризация способом k-среднего, нейронные сети и состязательный поиск.

Состязательный поиск

Безупречная информационная игра для 2-ух игроков с нулевой суммой и четкой информацией — это игра, в которой оба конкурента имеют всю доступную им информацию о состоянии игры и все, что является преимуществом для 1-го, становится потерей достоинства для другого. К таковым играм относятся крестики-нолики, Connect Four, шашки и шахматы. В данной нам главе вы узнаете, как сделать мощного искусственного конкурента, способного играться в такие игры. В сути, обсуждаемые способы в сочетании с современными вычислительными способностями разрешают создавать искусственных конкурентов, которые отлично играют в обыкновенные игры этого класса и способны играться в сложные игры, выходящие за границы способностей хоть какого соперника-человека.

8.1. Главные составляющие настольной игры

Как и при рассмотрении большинства наиболее сложных задач в прошлых главах, попытаемся создать решение как можно наиболее обобщенным. В случае состязательного поиска это значит, что наши методы поиска не должны зависеть от игры. Начнем с определения нескольких обычных базисных классов, которые выявляют состояние, нужное методам поиска. Потом сделаем подклассы базисных классов для определенных игр (крестики-нолики и Connect Four) и введем эти подклассы в методы поиска, чтоб они могли «играться» в эти игры. Вот базисные классы (листинг 8.1).

Листинг 8.1. Piece.java

Piece — это базисный класс для фигуры на доске в игре. Его иная роль — индикатор хода. Конкретно для этого нужно свойство opposite. Нам необходимо знать, чей ход следует за текущим ходом (листинг 8.2).

Листинг 8.2. Board.java

Класс Board является фактическим хранилищем состояния. Для хоть какой определенной игры, которую будут делать методы поиска, они должны уметь ответить на последующие вопросцы.

• Чей на данный момент ход?

• Какие ходы можно создать из текущей позиции согласно правилам?

• Выиграна ли на данный момент игра?

• Сыграна ли игра вничью?

• Создать ход, чтоб перейти из текущей в новейшую позицию.

• Оценить позицию, чтоб узреть, какой игрок имеет преимущество.

Любой способ и свойство класса Board являются реализацией 1-го из прошлых вопросцев либо действий. На языке игры класс Board можно было бы именовать Position, но мы используем это имя зачем-то наиболее определенного в любом из подклассов.

Класс Board имеет общий тип Move. Тип Move представляет собой ход в игре. Это быть может просто целое число. В таковых играх, как крестики-нолики и Connect Four, целое число представляет ход, указывая клеточку либо столбец, где обязана быть расположена фигура. В наиболее сложных играх для описания хода может потребоваться большее число, чем целое число. Move дозволяет классу Board представлять наиболее широкий диапазон игр.

8.2. Крестики-нолики

8.2.1. Управление состоянием игры в крестики-нолики

Давайте разработаем несколько структур, позволяющих выслеживать состояние игры в крестики-нолики по мере ее развития.

До этого всего нужен метод представления каждой клеточки на игровом поле. Будем употреблять перечисление TTTPiece — подкласс класса Piece. Клеточка в игре в крестики-нолики может иметь значение X, 0 либо быть пустой (в перечислении такие обозначаются E) (листинг 8.3).

Листинг 8.3. TTTPiece.java

В классе TTTPiece имеется свойство opposite, которое возвращает иной экземпляр TTTPiece. Это полезно для передачи хода от 1-го игрока к другому опосля того, как очередной ход игры завершен. Для представления ходов используем обыденное целое число, соответственное клеточке на поле, где был поставлен крестик либо нолик. Как вы помните, Move был определен в классе Board. Укажем, что Move при определении TTTPiece — целое число.

В игре в крестики-нолики существует девять позиций, образующих три ряда по три столбца. Для простоты эти девять позиций можно представить в виде одномерного перечня. То, какие клеточки получат какие номера (иными словами, индексы в массиве), не имеет значения, но мы будем придерживаться схемы, показанной на рис. 8.1.

Основным хранилищем состояния игры будет класс TTTBoard. Он выслеживает два элемента состояния: позицию, представленную вышеупомянутым одномерным перечнем, и игрока, который на данный момент делает ход (листинг 8.4).

Листинг 8.4. TTTBoard.java

Начальное состояние поля — такое, при котором еще не изготовлено ни 1-го хода (пустое поле). Конструктор без характеристик для TTTBoard инициализирует такую позицию, при которой 1-ый игрок готовится поставить X (обыденный 1-ый ход в игре). getTurn() показывает, чья очередь находится в текущей позиции, X либо O.

TTTBoard — это по соглашению неизменяемая структура данных: структуры TTTBoard не должны изменяться. Заместо этого всякий раз, когда нужно создать ход, будет генерироваться новенькая структура TTTBoard, позиция которой изменена с учетом хода. Потом это понадобится в методе поиска. При ветвлении поиска мы не сможем случаем поменять положение на поле, начиная с которого все еще анализируются потенциально вероятные ходы (листинг 8.5).

Листинг 8.5. TTTBoard.java (продолжение)

Допустимым ходом в игре является неважно какая пустая клеточка. getLegalMoves() отыскивает любые пустые клеточки на поле и возвращает их перечень (листинг 8.6).

Листинг 8.6. TTTBoard.java (продолжение)

Существует огромное количество методов просмотреть строки, столбцы и диагонали на поле игры, чтоб проверить, закончилась ли она победой. В показанной дальше реализации способа isWin()вкупе с его вспомогательным способом checkPos() это изготовлено средством агрессивно закодированной конструкции из &&, || и ==, которая кажется нескончаемой (листинг 8.7). Это не самый прекрасный код, но он обычной и делает свою работу.

Листинг 8.7. TTTBoard.java (продолжение)

Если все клеточки строки, столбца либо диагонали не пустые и содержат схожие элементы, то игра выиграна.

Игра закончена вничью, если она не выиграна и не осталось допустимых ходов (это свойство уже описано в способе isDraw() класса Board). В конце концов, нам нужен метод оценки определенной позиции и структурного вывода состояния поля (листинг 8.8).

Листинг 8.8. TTTBoard.java (продолжение)

В большинстве игр приходится вычислять позицию примерно, так как мы не можем пройти игру до самого конца, чтоб буквально найти, кто выиграет либо проиграет в зависимости от того, какие ходы будут изготовлены. Но в крестиках-ноликах достаточно маленькое место поиска, так что мы можем пройти его от хоть какой позиции до конца игры. Как следует, способ evaluate() может просто возвращать некоторое число, если игрок выиграл, наименьшее число — в случае ничьей и совершенно маленькое — в случае проигрыша.

8.2.2. Минимакс

Минимакс — это традиционный метод для поиска лучшего хода в играх с 2-мя игроками, нулевой суммой и хорошей информацией, таковых как крестики-нолики, шашки либо шахматы. Этот метод был расширен и изменен для остальных типов игр. Минимакс обычно реализуется с внедрением рекурсивной функции, в которой любой игрок обозначается как максимизирующий либо минимизирующий.

Максимизирующий игрок стремится отыскать ход, который приведет к наибольшему выигрышу. Но он должен учесть ходы минимизирующего игрока. Опосля каждой пробы максимизирующего игрока максимизировать выигрыш рекурсивно вызывается минимакс, чтоб отыскать ответ противника, который минимизирует максимизирующий выигрыш игрока. Это длится в обоих направлениях (максимизация, минимизация, максимизация и т. д.), пока не будет достигнут базисный вариант рекурсивной функции. Базисный вариант — это конечная позиция (выигрыш либо ничья) или достижение наибольшей глубины поиска.

Минимакс вычисляет стартовую позицию для максимизирующего игрока. Для способа evaluate() класса TTTBoard, если лучшая вероятная игра обеих сторон приведет к выигрышу максимизирующего игрока, ворачивается 1 балл. Если лучшая вероятная игра приведет к проигрышу, то ворачивается –1. В конце концов, если лучшая игра — это ничья, то ворачивается 0.

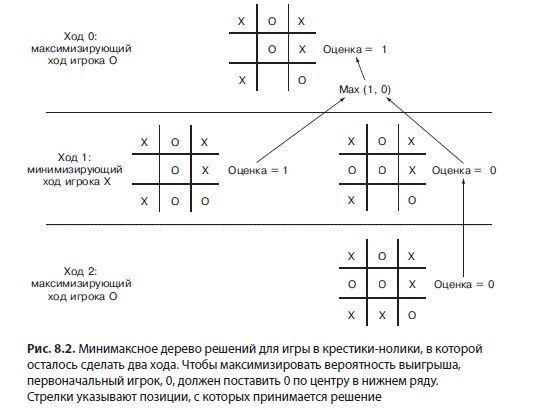
Эти числа ворачиваются при достижении базисного варианта. Потом они передаются через все рекурсивные вызовы, которые привели к базисному случаю. Чтоб максимизировать любой рекурсивный вызов, ввысь по рекурсии передаются лучшие вычисленные ходы. Чтоб минимизировать любой рекурсивный вызов, передаются худшие вычисленные ходы. Таковым образом строится дерево решений. На рис. 8.2 показано такое дерево, которое упрощает передачу данных ввысь по рекурсивным вызовам для игры, в которой осталось создать два хода.

В играх, имеющих очень глубочайшее место поиска, таковых как шашки и шахматы, чтоб достигнуть конечной позиции, минимакс останавливается опосля заслуги определенной глубины (выполнения данного количества ходов поиска, время от времени именуемого ply). Потом врубается функция оценки, использующая эвристику для оценки состояния игры. Чем лучше смотрится игра для первого игрока, тем выше присуждаемая ей оценка. Мы вернемся к данной нам концепции, когда будем дискуссировать игру Connect Four, которая имеет еще большее место поиска, чем крестики-нолики.

В листинге 8.9 представлена полная реализация функции minimax().

Листинг 8.9. Minimax.java

При любом рекурсивном вызове необходимо выслеживать позицию на поле независимо от того, максимизируем мы ее либо минимизируем и для кого пытаемся оценить позицию (originalPlayer).

1-ые несколько строк функции minimax() касаются базисного варианта — заключительной позиции (выигрыш, проигрыш либо ничья) либо очень достижимой глубины. Остальная часть функции обрабатывает рекурсивные случаи.

Один из рекурсивных случаев — это максимизация. В данной нам ситуации мы отыскиваем ход, который даст очень вероятную оценку. 2-ой рекурсивный вариант — минимизация: отыскиваем ход, который приведет к меньшей вероятной оценке. Как бы то ни было, эти два варианта чередуются, пока не будет достигнута финишная позиция либо наибольшая глубина поиска (базисный вариант).

К огорчению, мы не можем употреблять нашу реализацию minimax(), чтоб отыскать лучший ход для данной позиции, потому что функция возвращает оценку — значение с плавающей запятой. Оно не докладывает, какой наилучший 1-ый ход привел к данной оценке.

Заместо этого сделаем вспомогательную функцию findBestMove(), которая перебирает вызовы minimax() для всякого допустимого хода из данной позиции и дозволяет отыскать ход, который имел бы наивысшую оценку. Функцию findBestMove() можно представить как 1-ый максимизирующий вызов minimax(), но с отслеживанием исходных ходов (листинг 8.10).

Листинг 8.10. Minimax.java (продолжение)

Сейчас у нас все есть нужное, чтоб отыскать лучший вероятный ход для хоть какой позиции при игре в крестики-нолики.

Для Хаброжителей скидка 25% по купону — Java

По факту оплаты картонной версии книжки на e-mail высылается электрическая книжка.

Как перевернуть текст в Ворде в любом направлении – все методы

Разглядим 5 действующих методов, как можно перевернуть текст в Ворде.

MS Word – это одна из самых комфортных программ для сотворения и редактирования текстовых документов.

Юзерам доступно большущее количество функций: от обычного редактирования текста до сотворения таблиц, макетов, рисунков, примечаний и ссылок.

Функция переворота текста тоже доступна в программке, но её достаточно трудно отыскать.

Вы сможете регулировать угол поворота отдельных слов, предложений либо всего текста сходу.

Всего есть несколько методов, как это создать.

Метод 1 – Создать весь текст вертикальным

Если специфичность создаваемого вами документа предполагает написание всего текста вертикально, следует сходу настроить альбомную ориентацию странички.

Так вы можете просто напечатать подходящий текст без внедрения посторониих инструментов Ворда.

• Откройте документ Word;
• В верхней области меню перейдите во вкладку «Макет»;
• Кликните на пункт «Ориентация» и в выпадающем перечне нажмите на «Альбомная».

Размещение всего документа будет автоматом изменено. Если на страничке уже был текст, он тоже будет перевернут вертикально.

В меню «Макет» вы можете настроить поля либо применить поворот лишь для отдельных страничек документа.

Направьте внимание! На листе вся информация будет отображаться вертикально: не только лишь текст, да и рисунки. Если необходимо перевернуть картину под остальным углом, довольно надавить на неё правой кнопкой, перейти во вкладку редактирования и избрать тип поворота.

Метод 2 – Внедрение таблиц

В MS Word юзеры могут создавать любые таблицы и заполнять их не только лишь текстом, да и графическим контентом.

Поворот текста при помощи таблиц дозволяет настроить хоть какой угол отображения знаков. Рамки таблицы постоянно можно скрыть.

• Сделайте таблицу при помощи меню «Вставка»-«Таблица»;
• Потом напечатайте текст в одной из ячеек и выделите его;
• Кликните на выделенном объекте правой клавишей мышки и во всплывающем перечне действий изберите «Направление текста»;

• Раскроется окно опции отображения содержимого. Изберите один из 3-х типов поворота, проверьте эталон и подтвердите действие;

Если для вас необходимо повернуть текст, но нет необходимости создавать таблицу, постоянно можно нарисовать лишь одну ячейку, а потом стремительно убрать видимость её границ.

Для удаления очертаний табличек нажмите на левый верхний угол элемента. Это выделит всю таблицу.

Потом кликните на правую клавишу мышки и изберите в меню «Границы и заливка».

Во вкладке выбора типа границы выделите «нет» и примените конфигурации.

При помощи этого метода можно просто поворачивать формулы, спецсимволы и остальные элементы, для которых недозволено применить угол направления без таблицы.

Метод 3 – Надпись в фигуре

Снутри документа можно создавать отдельные полотна с фигурами либо блоками текста.

Таковой блок можно расположить в любом месте странички. Текст будет перевернут под необходимым углом.

Ниже приведен пример работы с блоками в MS Word:

• Откройте документ и в верхней области программки кликните на вкладку «Вставка»;
• Изберите поле «Фигуры»;
• Посреди перечня всех частей выберете значок «Надпись»;

• Дальше на страничке покажется пустой блок, снутри которого для вас необходимо набрать текст. При помощи вкладки редактирования можно убрать либо настроить границы фигуры, избрать заливку и форму;
• Для поворота фигуры необходимо надавить левой клавишей мышки на область зеленоватого круга вверху текстового блока. Удерживая кнопку, вращайте элемент, пока текст не будет отображаться необходимым для вас образом;

Таковой метод комфортен при разработке блок-схем, разных дизайнов брошюр, дизайна отчетов и иных видов документов.

Направьте внимание, если вы создаете несколько блоков, чтоб они не двинулись, их можно группировать.

Для этого выделите сходу несколько фигур с текстом, нажмите на их правой клавишей и изберите «Группировать».

Создастся единое полотно, которое можно перемещать по тексту.

Метод 4 – Поворот строки

Если необходимо просто повернуть строчку ввысь тормашками, а не поворачивать текст под хоть каким углом, можно опять употреблять фигуру.

• Выделите фигуру с вписанным текстом и перейдите во вкладку программки «Макет»;
• Дальше изберите поле «Размер» и в строке «Поворот» вчеркните градус вращения. Чтоб строчка отображалась ввысь ногами необходимо выставить 180 градусов;

• Чтоб удалить контур текстового поля, кликните на фигуре правой клавиш мышки и нажмите на «Формат фигуры» — «Убрать контур».

В итоге текст будет отображаться как показано ниже. Около имеющегося блока можно писать текст в обыкновенном режиме набора.

Все описанные выше деяния можно применить к объектам стиля WordArt.

Напомним, что WordArt – это режим сотворения стилизованных надписей, который можно настроить через вкладку программки «Вставка».

Метод 5 – Внедрение SmartArt

SmartArt – это база для сотворения инфографики с уже готовыми шаблонами. В первый раз функция возникла в версии MS Word 2007.

При помощи Смарт Арт можно создавать списки, схемы, диаграммы, матрицы, пирамиды, иерархию, циклы и много остальных объектов.

Текст блоках SmartArt тоже можно перевернуть. Для этого откройте пункт меню «Вставка» и кликните на кнопку прибавления инфографики.

В левой части открывшегося окна показываются группы, а в правой – перечень доступных дизайнов. Изберите понравившийся элемент и нажмите «ОК».

Потом на страничке документа изберите ячейку, размещение текста которой необходимо отредактировать. Нажмите на него правой клавишей мышки.

Дальше изберите «Характеристики анимации»:

В новеньком окне перейдите во вкладку «Надпись» и справа найдите строчку «Направление текста».

Всего доступно три варианта поворота – Горизонтальный, на 90 градусов и на 270 градусов.

Печать зеркального текста

Если у вас есть готовый текстовый документ Ворд и его необходимо напечатать таковым образом, чтоб на листе текст отображался зеркально, это можно создать и без редактирования страничек в программке.

Довольно поменять опции самой печати.

Откройте пункт меню «Файл» и кликните на «Печать».

В новеньком окне найдите надстройку «Характеристики печати» и отметьте галочкой пункт «Зеркальные поля».

Все описанные в статье методы поворота текста будут работать во всех версиях программки MS Word.

Различаться может лишь размещение вкладок приложения. Направьте внимание, чтоб главный и перевернутый текст смотрелись нормально, необходимо удалить междустрочные интервалы меж абзацами и таблицей либо меж абзацами и фигурой.

В неприятном случае, отступы меж этими объектами будут очень очень кидаться в глаза.

Если посреди текста, который необходимо перевернуть, есть формула, необходимо употреблять лишь методом с таблицами.

Нередко способ с блоками не работает для сложных высотных формул и особых знаков.