Как применять функцию выбросов в Excel — Вокруг-Дом — 2021
Когда вы анализируете данные, выбросы могут исказить результаты и создать их наименее надежными. К примеру, если одно либо несколько ваших значений значительно выше, чем у большинства данных, они наращивают среднее значение, что может не отражать данные в целом. Потому удаление этих удаленных точек данных является принципиальным шагом в выполнении надежных статистических расчетов. Без выделенной функции выбросов самый обычной метод выполнить тест выбросов в Excel — это применять межквартильный спектр для определения выбросов, но вы также сможете применять функцию Trimmean для аппроксимации такого же результата.
кредит: nd3000 / iStock / GettyImages
Расчет межквартильного спектра
Межквартильный спектр данных — это спектр, охватываемый «квадратом» на графике «квадрат и ус», либо, поточнее, итог вычитания значения для первого квартиля из данных третьего квартиля. Excel содержит встроенную функцию для расчета хоть какого квартиля для ваших данных. Найдите запасную ячейку и введите «= QUARTILE (спектр данных, число квартилей)» и расположите спектр ячеек для ваших данных, где обозначено «спектр данных», и подходящий квартиль, где говорится «квартиль» число."
К примеру, если у вас есть данные в ячейках с A2 по A101, и вы желаете получить значение для первого квартиля, введите «= QUARTILE (A2: A101, 1)», чтоб отыскать это значение. Для первой части аргумента вы сможете выделить надлежащие ячейки мышью, но опосля запятой для вас необходимо указать хотимое число квартилей. Для третьего квартиля с теми же данными введите «= QUARTILE (A2: A101, 3)», чтоб получить итог.
Используя другую пустую ячейку, вычтите значение первой ячейки квартиля из значения третьей ячейки квартиля. Если 1-ый квартиль находится в ячейке C2, а 3-ий квартиль находится в ячейке D2, введите «= D2-C2», чтоб получить итог. Это межквартильный размах.
Анализ выбросов в Excel
Чтоб отыскать выбросы, сейчас вы сможете применять межквартильный спектр в формуле выброса, в котором говорится, что верхний предел данных — это значение третьего квартиля плюс 1,5-кратный межквартильный спектр, а нижний предел — значение первого квартиля. минус 1,5 раза межквартильный спектр.
Если 1-ое квартильное значение находится в C2, третье квартильное значение находится в ячейке D2, а межквартильный спектр находится в ячейке E2, вы должны набрать "= C2- (1.5 E2) «отыскать нижний предел» и = D2 + (1,5 E2) "чтоб отыскать верхний предел. В общем, вы вводите" = 1-ый квартиль — (1,5 межквартильный спектр) «отыскать нижний предел и» = 3-ий квартиль + (1,5 interquartile range) ", чтоб отыскать верхний предел.
Все, что ниже нижнего предела либо выше верхнего предела, является выбросом.
Чтоб окончить тест выбросов в Excel, используйте логическую функцию «ИЛИ», чтоб найти, какие значения в вашем классе данных являются выбросами действенным методом. Введите «= ИЛИ (ячейка данных> верхний предел, ячейка данных <нижний предел)», чтоб отыскать выбросы с надлежащими ссылками на ячейки заместо величин в квадратных скобках. К примеру, если данные находятся в ячейках с A2 по A101, верхний предел находится в ячейке F2, а нижний предел находится в ячейке G2, перейдите в ячейку B2 и введите «= OR (A2> $ F $ 2, A2 <$ G». $ 2) «применять функцию (где знаки бакса перед« F »,« G »и« 2 »молвят Excel, что это не обязано поменяться при перетаскивании формулы вниз).
Если значение в A2 выше верхнего предела либо ниже нижнего предела, отображается «ИСТИНА», что показывает на то, что значение является выбросом. Вы сможете перетащить эту формулу вниз, щелкнув в правом нижнем углу ячейки с формулой и перетащив ее вниз, чтоб она заканчивалась рядом с крайней ячейкой данных, чтоб выполнить схожие вычисления для каждой точки данных.
Вы также сможете выделить данные и перейти к «Условному форматированию» в разделе «Стили» на вкладке «Основная», если вы желаете поменять форматирование выбросов. Изберите «Новое правило» и выделите опцию «Применять формулу, чтоб найти, какие ячейки форматировать». Введите ту же формулу, что и в прошлом абзаце, а потом нажмите параметр «Формат», чтоб избрать неповторимое форматирование для выбросов.
Внедрение Trimmean
Функция «Trimmean» — это наиболее обычной метод определения выбросов. Введите «= TRIMMEAN (спектр данных, пропорция к обрезке)», чтоб применять функцию, с спектром ячеек, содержащим данные заместо «спектр данных» и десятичным процентом, который вы желаете обрезать, где он гласит « пропорция к отделке. " Это удаляет экстремальные значения сверху и снизу, а потом вычисляет среднее значение на базе оставшихся. Таковым образом, если вы урежете 10 процентов, то перед вычислением среднего значения будут удалены верхние 5 процентов и нижние 5 процентов.
Если данные идут от A2 до A101, и вы желаете обрезать последние 5 процентов значений, введите «= TRIMMEAN (A2: A101, 0,05)», чтоб отыскать скорректированное среднее значение. Вы сможете обрезать 15 процентов, написав "= TRIMMEAN (A2: A101, 0.15)".
Какую функцию вы сможете применять для расчета валовой платы в Excel?
Совокупная зарплата — это общая сумма валютной компенсации, которую работник получает за период оплаты. В валовую оплату не входят неденежные пособия, такие как мед страхование, .
Как применять функцию «ЕСЛИ» в Excel
Оператор IF в Excel дозволяет делать разные операции с ячейками электрической таблицы в зависимости от того, являются ли условия в остальных ячейках логически настоящими либо неверными. .
Как применять функцию чтения вслух в Microsoft Excel на Windows 10
Желаете прочесть статью либо электрическую книжку? Тут вы узнаете, как отыскать и применять функцию «Читать вслух» в Microsoft Edge в Windows 10.
Дисперсия характеристики, формула вычисления дисперсии дискретной случайной величины, виды, правило и примеры расчетов, онлайн-калькулятор
В разных научных дисциплинах словосочетание «дисперсия это» охарактеризовывает не достаточно идентичные понятия. С латыни «dispersio» переводится как «рассеяние».
В физике, к примеру, значит связь фазовой скорости волны с частотой. В химии обрисовывает несмешиваемые субстанции. В биологии – обилие признаков популяции.
В данной статье пойдет речь о математической трактовке. Рассматривается как одно из параметров случайных величин.
Что такое дисперсия в статистике
Статистика, в частности, оперирует рядами данных, характеризующих какой-нибудь признак, явление. Интересует их изменение.
Вариация представляет собой отличие величин схожего показателя у различных предметов. Ее исследование дозволит осознать предпосылки дефектов, рассматривать их и в некий мере предсказывать. Также станет вероятным выявить причины, действующие на значения, отсеяв случайные.
Свойства равномерного распределения представлены на картинке:
При значимом объеме статистики, средняя величина разумеется близка к обычной. О этом молвят и законы распределения. Отличия от нее будут являться беспристрастной чертой.
Лишь вот отрицательные значения этих разбросов будут сбивать с толку при расчетах, погашая положительные. А оставлять только модули – для математика не корректно. Навязывается возвести в четную степень, а конкретно – во вторую.
Решение оказалось не только лишь комфортным. Оно открыло бо́льшие способности в исследовании отклонений. А важны конкретно они, так как сама по для себя средняя не достаточно что дает.
В качестве 1-го из принципиальных характеристик варианты, вводится понятие «дисперсия» – усредненный квадрат отклонений численных значений каких-то событий от средней величины.
Коротко записывается D[X] в русских источниках и Var[X] (от «variance») в британских. В статистических выкладках употребляется σ 2 .
Никакого приятного смысла величина не несет. Другое дело, среднее квадратическое отклонение – корень квадратный из дисперсии.
Виды дисперсии дискретной случайной величины
Для анализа данных цифр в таком виде недостаточно. Еще больше можно выдавить из последовательности, если разбить ее на группы по определенному признаку.
Общая дисперсия
Как можно увидеть, вычисленная по приведенному выше определению величина охарактеризовывает отличия в целом. Без учета определяющих вариацию причин. Точнее, с учетом всех, включая совсем случайные. Потому и именуется «общей» и рассчитывается по формулам, обозначенным ниже.
Обычная дисперсия, без разделения на группы:
Либо в несколько перевоплощенном виде:
Взвешенная дисперсия, для вариационного ряда:
где xi – значение из ряда;
fi – частота, количество повторений;
n – число вариантов.
Черта сверху показывает на среднюю величину.
Межгрупповая дисперсия
Охарактеризовывает систематическое отклонение, возникающее из-за фактора, по которому выполнялось выделение признаков в группы. Потому также именуется «факторной».
Как отыскать данную дисперсию? По формуле:
где k – количество групп;
nj – частей в группе с индексом j.
Внутригрупповая дисперсия
Возникает по беспорядочной причине, не связанной с предпосылкой изготовленной подборки. Неучтенный фактор. Еще обозначается как «остаточная».
К примеру, рассматривается количество выпущенных деталей в месяц каждым фрезеровщиком цеха.
В качестве аспекта отбора в группу избираем возраст оборудования. Он-то и не будет влиять на производительность снутри выборки: там станки у всех фактически схожие.
Если вычислить среднюю величину от всех групповых,
то получим характеристику случайного разброса. Другими словами, составляющую варианты, зависящую от что угодно, не считая фактора отбора.
Связь
В согласовании с правилом сложения, общая D[X] включает средние выражения остаточной и факторной. И это разумно, так как учитывает и случайное изменение в группе, и систематическое в факторной.
Характеристики дисперсии
Если последовательность состоит из схожих чисел, то D[X] будет нулевой.
Уменьшение всех значений на постоянную величину на дисперсию не влияет. По другому говоря, высчитать σ 2 можно по отклонениям от фиксированного числа.
Уменьшение всех цифр в k раз приведет к падению D[X] в k 2 раз. Можно, к примеру, иметь в виду значения в метрах, а итог вычислить в футах. Довольно учитывать один раз то, на что следует помножить.
Средний квадрат отклонений от неизменной величины X различается в огромную сторону от такого же с внедрением среднего значения. Разница составит (Xcр – X) 2 .
Характеристики вариантов
Не считая размаха (различия наибольшего и малого значений), среднего линейного и дисперсии, конфигурации описываются коэффициентом варианты:
Оценить масштаб разброса проще по относительной величине. Тем наиболее, что измеряются в одних единицах.
Пример расчета дисперсии
Компания объявила конкурсный отбор для приема служащих. В качестве аспекта принят стаж работы по специальности. Приведем начальные данные и расчеты.
По другой формуле:
Заключение
Статистика оперирует значительными размерами данных. Вариация, как одно из главных понятий – не исключение. И дисперсия в качестве главный свойства.
Для упрощения расчетов существует масса онлайн калькуляторов. Имеется упомянутый инструмент в MS Excel.
Дисперсия, виды и характеристики дисперсии
Дисперсия в статистике находится как среднее квадратическое отклонение личных значений признака в квадрате от средней арифметической. Зависимо от начальных данных она определяется по формулам обычной и взвешенной дисперсий:
1. Обычная дисперсия (для несгруппированных данных) рассчитывается по формуле:
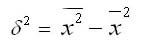2. Взвешенная дисперсия (для вариационного ряда):
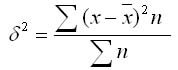где n — частота (повторяемость фактора Х)
Пример нахождения дисперсии
На данной страничке описан обычный пример нахождения дисперсии, также Вы сможете поглядеть остальные задачки на её нахождение
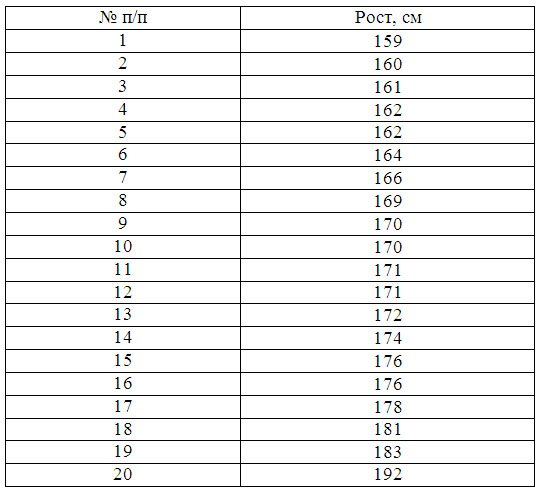
Пример 1. Имеются последующие данные по группе из 20 студентов заочного отделения. Необходимо выстроить интервальный ряд распределения признака, высчитать среднее значение признака и изучить его дисперсию
Построим интервальную группировку. Определим размах интервала по формуле:
где X max– наибольшее значение группировочного признака;
X min–малое значение группировочного признака;
n – количество интервалов:
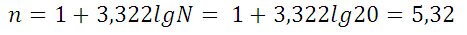Принимаем n=5. Шаг равен: h = (192 — 159)/ 5 = 6,6
Составим интервальную группировку
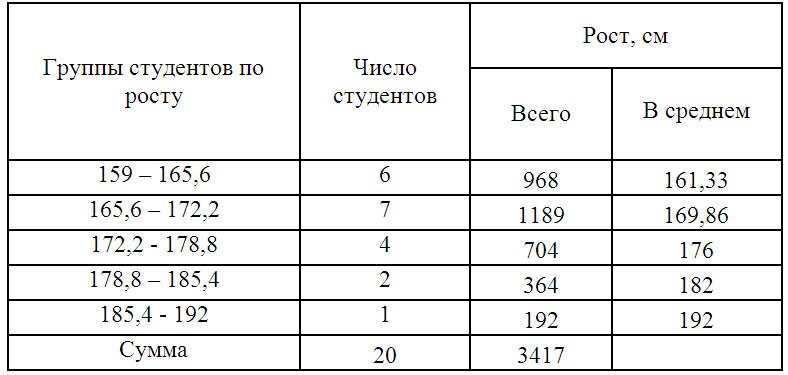
Для последующих расчетов построим вспомогательную таблицу:
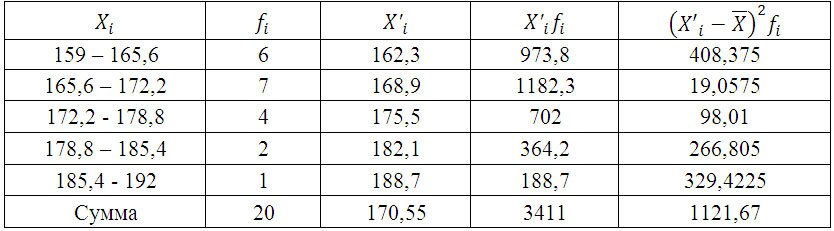X’i– середина интервала. (к примеру середина интервала 159 – 165,6 = 162,3)
Среднюю величину роста студентов определим по формуле средней арифметической взвешенной:
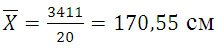Определим дисперсию по формуле:
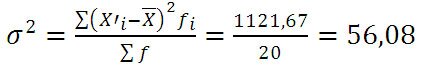
Формулу дисперсии можно конвертировать так:
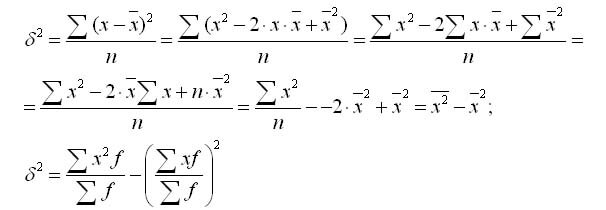
Из данной формулы следует, что дисперсия равна разности средней из квадратов вариантов и квадрата и средней.
Дисперсия в вариационных рядах с равными интервалами по способу моментов быть может рассчитана последующим методом при использовании второго характеристики дисперсии (разделив все варианты на величину интервала). Определении дисперсии, вычисленной по способу моментов, по последующей формуле наименее трудоемок:
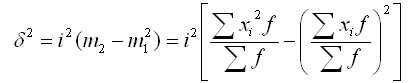
где i — величина интервала;
А — условный ноль, в качестве которого комфортно применять середину интервала, владеющего большей частотой;
m1 — квадрат момента первого порядка;
m2 — момент второго порядка
Дисперсия альтернативного признака (если в статистической совокупы признак меняется так, что имеются лишь два взаимно исключающих друг дружку варианта, то таковая изменчивость именуется другой) быть может вычислена по формуле:
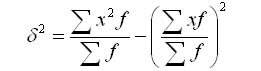
Подставляя в данную формулу дисперсии q =1- р, получаем:
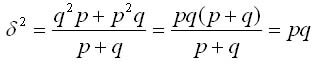
Виды дисперсии
Общая дисперсия определяет вариацию признака по всей совокупы в целом под воздействием всех причин, обуславливающих эту вариацию. Она приравнивается среднему квадрату отклонений отдельных значений признака х от общего среднего значения х и быть может определена как обычная дисперсия либо взвешенная дисперсия.
Внутригрупповая дисперсия охарактеризовывает случайную вариацию, т.е. часть варианты, которая обоснована воздействием неучтенных причин и не зависящую от признака-фактора, положенного в основание группировки. Таковая дисперсия равна среднему квадрату отклонений отдельных значений признака снутри группы X от средней арифметической группы и быть может вычислена как обычная дисперсия либо как взвешенная дисперсия.
Таковым образом, внутригрупповая дисперсия определяет вариацию признака снутри группы и определяется по формуле:
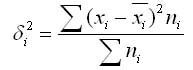
где хi — групповая средняя;
ni — число единиц в группе.
К примеру, внутригрупповые дисперсии, которые нужно найти в задачке исследования воздействия квалификации рабочих на уровень производительности труда в цехе демонстрируют варианты выработки в каждой группе, вызванные всеми вероятными факторами (техническое состояние оборудования, обеспеченность инструментами и материалами, возраст рабочих, интенсивность труда и т.д.), не считая различий в квалификационном разряде (снутри группы все рабочие имеют одну и ту же квалификацию).
Средняя из снутри групповых дисперсий отражает случайную вариацию, т. е. ту часть варианты, которая происходила под воздействием всех иных причин, кроме фактора группировки. Она рассчитывается по формуле:
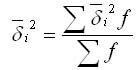
Межгрупповая дисперсия охарактеризовывает периодическую вариацию действенного признака, которая обоснована воздействием признака-фактора, положенного в основание группировки. Она приравнивается среднему квадрату отклонений групповых средних от общей средней. Межгрупповая дисперсия рассчитывается по формуле:
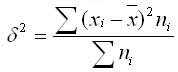
Правило сложения дисперсии в статистике
Согласно правилу сложения дисперсий общая дисперсия равна сумме средней из внутригрупповых и межгрупповых дисперсий:
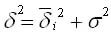
Смысл этого правила заключается в том, что общая дисперсия, которая возникает под воздействием всех причин, приравнивается сумме дисперсий, которые появляются под воздействием всех иных причин, и дисперсии, возникающей за счет фактора группировки.
Пользуясь формулой сложения дисперсий, можно найти по двум известным дисперсиям третью неведомую, также судить о силе воздействия группировочного признака.
Характеристики дисперсии
1. Если все значения признака уменьшить (прирастить) на одну и ту же постоянную величину, то дисперсия от этого не поменяется.
2. Если все значения признака уменьшить (прирастить) в одно и то же число раз n, то дисперсия соответственно уменьшится (прирастить) в n^2 раз.
