Расчет дисперсии в Microsoft Excel

Блог о программке Microsoft Excel: приемы, хитрости, секреты, трюки

Как расчитать дисперсию в Excel при помощи функции ДИСП.В

Дисперсия — это мера рассеяния, описывающая сравнительное отклонение меж значениями данных и средней величиной. Является более применяемой мерой рассеяния в статистике, вычисляемая методом суммирования, возведенного в квадрат, отличия всякого значения данных от средней величины. Формула для вычисления дисперсии представлена ниже:

s 2 – дисперсия подборки;

x_ср — среднее значение подборки;

n — размер подборки (количество значений данных),

(x_i – x_ср) — отклонение от средней величины для всякого значения набора данных.

Для наилучшего осознания формулы, разберем пример. Я не весьма люблю готовку, потому занятием сиим занимаюсь очень изредка. Тем не наименее, чтоб не умереть с голоду, временами мне приходится подступать к плите для реализации плана по насыщению моего организма белками, жирами и углеводами. Набор данных, редставленный ниже, указывает, сколько раз Ренат готовит еду любой месяц:

Первым шагом при вычислении дисперсии является определение среднего значения подборки, которое в нашем примере приравнивается 7,8 раза в месяц. Другие вычисления можно облегчить при помощи последующей таблицы.

Финишная фаза вычисления дисперсии смотрится так:

Для тех, кто любит создавать все вычисления за один раз, уравнение будет смотреться последующим образом:

Внедрение способа «сырого счета» (пример с готовкой)

Существует наиболее действенный метод вычисления дисперсии, узнаваемый как способ «сырого счета». Хотя с первого взора уравнение может показаться очень массивным, по сути оно не такое уж ужасное. Сможете в этом удостовериться, а позже и решите, какой способ для вас больше нравится.

— сумма всякого значения данных опосля возведения в квадрат,

— квадрат суммы всех значений данных.

Не теряйте рассудок прямо на данный момент. Разрешите представить все это в виде таблицы, тогда и вы увидите, что вычислений тут меньше, чем в прошлом примере.

Видите ли, итог вышел этот же, что и при использовании предшествующего способа. Плюсы данного способа стают явными по мере роста размера подборки (n).

Расчет дисперсии в Excel

Как вы уже, наверняка, додумались, в Excel находится формула, позволяющая высчитать дисперсию. При этом, начиная с Excel 2010 можно отыскать 4 разновидности формулы дисперсии:

1) ДИСП.В – Возвращает дисперсию по выборке. Логические значения и текст игнорируются.

2) ДИСП.Г — Возвращает дисперсию по генеральной совокупы. Логические значения и текст игнорируются.

3) ДИСПА — Возвращает дисперсию по выборке с учетом логических и текстовых значений.

4) ДИСПРА — Возвращает дисперсию по генеральной совокупы с учетом логических и текстовых значений.

Для начала разберемся в разнице меж подборкой и генеральной совокупой. Предназначение описательной статистики состоит в том, чтоб суммировать либо показывать данные так, чтоб оперативно получать общую картину, так сказать, обзор. Статистический вывод дозволяет созодать умозаключения о какой-нибудь совокупы на базе подборки данных из данной нам совокупы. Совокупа представляет собой все вероятные финалы либо измерения, представляющие для нас энтузиазм. Подборка — это подмножество совокупы.

К примеру, нас интересует совокупа группы студентов 1-го из Русских ВУЗов и нам нужно найти средний бал группы. Мы можем посчитать среднюю успеваемость студентов, тогда и приобретенная цифра будет параметром, так как в наших расчетах будет задействована целая совокупа. Но, если мы желаем высчитать средний бал всех студентов нашей страны, тогда эта группа будет нашей подборкой.

Разница в формуле расчета дисперсии меж подборкой и совокупой заключается в знаменателе. Где для подборки он будет приравниваться (n-1), а для генеральной совокупы лишь n.

Сейчас разберемся с функциями расчета дисперсии с окончаниями А, в описании которых сказано, что при расчете учитываются текстовые и логические значения. В этом случае при расчете дисперсии определенного массива данных, где встречаются не числовые значения, Excel будет интерпретировать текстовые и неверные логические значения как равными 0, а настоящие логические значения как равными 1.

Итак, если у вас есть массив данных, высчитать его дисперсию ни составит никакого труда, воспользовавшись одной из вышеперечисленных функций Excel.

Как высчитать дисперсию в Excel

Из предшествующей статьи мы узнали о таковых показателях, как размах варианты, межквартильный размах и среднее линейное отклонение. В данной нам статье изучим дисперсию, среднеквадратичное отклонение и коэффициент варианты.

Дисперсия

Дисперсия случайной величины – это один из главных характеристик в статистике. Он отражает меру разброса данных вокруг средней арифметической.

На данный момент маленький экскурс в теорию вероятностей, которая лежит в базе математической статистики. Как и матожидание, дисперсия является принципиальной чертой случайной величины. Если матожидание отражает центр случайной величины, то дисперсия дает характеристику разброса данных вокруг центра.

Формула дисперсии в теории вероятностей имеет вид:

Другими словами дисперсия — это математическое ожидание отклонений от математического ожидания.

На практике при анализе выборок математическое ожидание, обычно, не понятно. Потому заместо него употребляют оценку – среднее арифметическое. Расчет дисперсии создают по формуле:

s 2 – выборочная дисперсия, рассчитанная по данным наблюдений,

X – отдельные значения,

X̅– среднее арифметическое по выборке.

Необходимо отметить, что у такового расчета дисперсии есть недочет – она выходит смещенной, т.е. ее математическое ожидание не равно настоящему значению дисперсии. Подробней о этом тут. Но при увеличении размера подборки она все-же приближается к собственному теоретическому аналогу, т.е. является асимптотически не смещенной.

Ординарными словами дисперсия – это средний квадрат отклонений. Другими словами сначала рассчитывается среднее значение, потом берется разница меж каждым начальным и средним значением, возводится в квадрат, складывается и потом делится на количество значений в данной совокупы. Разница меж отдельным значением и средней отражает меру отличия. В квадрат возводится для того, чтоб все отличия стали только положительными числами и чтоб избежать взаимоуничтожения положительных и отрицательных отклонений при их суммировании. Потом, имея квадраты отклонений, просто рассчитываем среднюю арифметическую. Средний – квадрат – отклонений. Отличия возводятся в квадрат, и считается средняя. Сейчас вы понимаете, как отыскать дисперсию.

Расчет дисперсии в Excel

Генеральную и выборочную дисперсии просто высчитать в Excel. Есть особые функции: ДИСП.Г и ДИСП.В соответственно.

В чистом виде дисперсия не употребляется. Это вспомогательный показатель, который нужен в остальных расчетах. К примеру, в проверке статистических гипотез либо расчете коэффициентов корреляции. Отсюда хорошо бы знать математические характеристики дисперсии.

Характеристики дисперсии

Свойство 1. Дисперсия неизменной величины A равна (нулю).

Свойство 2. Если случайную величину помножить на постоянную А, то дисперсия данной нам случайной величины возрастет в А 2 раз. Иными словами, неизменный множитель можно вынести за символ дисперсии, возведя его в квадрат.

Свойство 3. Если к случайной величине добавить (либо отнять) постоянную А, то дисперсия остается постоянной.

Свойство 4. Если случайные величины X и Y независимы, то дисперсия их суммы равна сумме их дисперсий.

Свойство 5. Если случайные величины X и Y независимы, то дисперсия их различия также равна сумме дисперсий.

Если из дисперсии извлечь квадратный корень, получится среднеквадратичное (обычное) отклонение (сокращенно СКО). Встречается заглавие среднее квадратичное отклонение и сигма (от наименования греческой буковкы). Общая формула обычного отличия в арифметике последующая:

На практике формула обычного отличия последующая:

Как и с дисперсией, есть и незначительно иной вариант расчета. Но с ростом подборки разница исчезает.

Расчет cреднеквадратичного (обычного) отличия в Excel

Для расчета обычного отличия довольно из дисперсии извлечь квадратный корень. Но в Excel есть и готовые функции: СТАНДОТКЛОН.Г и СТАНДОТКЛОН.В (по генеральной и выборочной совокупы соответственно).

Среднеквадратичное отклонение имеет те же единицы измерения, что и анализируемый показатель, потому является сравнимым с начальными данными.

Значение обычного отличия зависит от масштаба самих данных, что не дозволяет ассоциировать вариабельность различных подборках. Чтоб убрать воздействие масштаба, нужно высчитать коэффициент варианты по формуле:

По нему можно ассоциировать однородность явлений даже с различным масштабом данных. В статистике принято, что, если значение коэффициента варианты наименее 33%, то совокупа считается однородной, если больше 33%, то – неоднородной. В действительности, если коэффициент варианты превосходит 33%, то специально ничего созодать по этому поводу не надо. Это информация для общего представления. В общем коэффициент варианты употребляют для оценки относительного разброса данных в выборке.

Расчет коэффициента варианты в Excel

Расчет коэффициента варианты в Excel также делается делением обычного отличия на среднее арифметическое:

Коэффициент варианты обычно выражается в процентах, потому ячейке с формулой можно присвоить процентный формат:

Коэффициент осцилляции

Очередной показатель разброса данных на сей день – коэффициент осцилляции. Это соотношение размаха варианты (различия меж наибольшим и наименьшим значением) к средней. Готовой формулы Excel нет, потому придется скомпоновать три функции: МАКС, МИН, СРЗНАЧ.

Коэффициент осцилляции указывает степень размаха варианты относительно средней, что также можно употреблять для сопоставления разных наборов данных.

Таковым образом, в статистическом анализе существует система характеристик, отражающих разброс либо однородность данных.

Ниже видео о том, как посчитать коэффициент варианты, дисперсию, обычное (среднеквадратичное) отклонение и остальные характеристики варианты в Excel.

Онлайн курс

Статистика в MS Excel

Корпоративный тренинг

Статистика в MS Excel

Поделиться в соц сетях:

• <ss>2</ss>
• <ss> </ss>
• <ss> </ss>
• <ss>1</ss>
• <ss> </ss>
• <ss> </ss>
• <ss> </ss>
• <ss> </ss>
• <ss> </ss>

Вычисление дисперсии

Дисперсия – это показатель варианты, который представляет собой средний квадрат отклонений от математического ожидания. Таковым образом, он выражает разброс чисел относительно среднего значения. Вычисление дисперсии может проводиться как по генеральной совокупы, так и по выборочной.

Метод 1: расчет по генеральной совокупы

Для расчета данного показателя в Excel по генеральной совокупы применяется функция ДИСП.Г. Синтаксис этого выражения имеет последующий вид:

Всего быть может использовано от 1 до 255 аргументов. В качестве аргументов могут выступать, как числовые значения, так и ссылки на ячейки, в которых они содержатся.

Поглядим, как вычислить это значение для спектра с числовыми данными.

1. Производим выделение ячейки на листе, в которую будут выводиться итоги вычисления дисперсии. Щелкаем по кнопочке «Вставить функцию», размещенную слева от строчки формул.
2. Запускается Мастер функций. В группы «Статистические» либо «Полный алфавитный список» исполняем поиск аргумента с наименованием «ДИСП.Г». Опосля того, как отыскали, выделяем его и щелкаем по кнопочке «OK».
3. Производится пуск окна аргументов функции ДИСП.Г. Устанавливаем курсор в поле «Число1». Выделяем на листе спектр ячеек, в котором содержится числовой ряд. Если таковых диапазонов несколько, то можно также употреблять для занесения их координат в окно аргументов поля «Число2», «Число3» и т.д. Опосля того, как все данные внесены, нажимаем на клавишу «OK».
4. Как лицезреем, опосля этих действий делается расчет. Результат вычисления величины дисперсии по генеральной совокупы выводится в за ранее обозначенную ячейку. Это конкретно та ячейка, в которой конкретно находится формула ДИСП.Г.

Урок: Мастер функций в Эксель

Метод 2: расчет по выборке

В отличие от вычисления значения по генеральной совокупы, в расчете по выборке в знаменателе указывается не полное количество чисел, а на одно меньше. Это делается в целях корректировки погрешности. Эксель учитывает данный аспект в специальной функции, которая создана для данного вида вычисления – ДИСП.В. Её синтаксис представлен последующей формулой:

Количество аргументов, как и в предшествующей функции, тоже может колебаться от 1 до 255.

1. Выделяем ячейку и таковым же методом, как и в предшествующий раз, запускаем Мастер функций.
2. В группы «Полный алфавитный список» либо «Статистические» отыскиваем наименование «ДИСП.В». Опосля того, как формула найдена, выделяем её и делаем клик по кнопочке «OK».
3. Делается пуск окна аргументов функции. Дальше поступаем стопроцентно аналогичным образом, как и при использовании предшествующего оператора: устанавливаем курсор в поле аргумента «Число1» и выделяем область, содержащую числовой ряд, на листе. Потом щелкаем по кнопочке «OK».
4. Итог вычисления будет выведен в отдельную ячейку.

Урок: Остальные статистические функции в Эксель

Как лицезреем, программка Эксель способна в значимой мере облегчить расчет дисперсии. Эта статистическая величина быть может рассчитана приложением, как по генеральной совокупы, так и по выборке. При всем этом все деяния юзера практически сводятся лишь к указанию спектра обрабатываемых чисел, а основную работу Excel делает сам. Непременно, это сбережет существенное количество времени юзеров. Мы рады, что смогли посодействовать Для вас в решении препядствия. Опишите, что у вас не вышло. Наши спецы постараются ответить очень стремительно.

Посодействовала ли для вас эта статья?

Цель данной статьи показать, как математические формулы, с которыми вы сможете столкнуться в книжках и статьях, разложить на простые функции в Excel.

В данной статье мы разберем формулы среднеквадратического отличия и дисперсии и рассчитаем их в Excel.

Перед тем как перебегать к расчету среднеквадратического отличия и разбирать формулу, лучше разобраться в простых статистических показателях и обозначениях.

Рассматривая формулы моделей прогнозирования, мы встретимся со последующими показателями:

Факторный и дисперсионный анализ в Excel с автоматизацией подсчетов

Чтоб проанализировать изменчивость признака под действием контролируемых переменных, применяется дисперсионный способ.

Для исследования связи меж значениями – факторный способ. Разглядим подробнее аналитические инструменты: факторный, дисперсионный и двухфакторный дисперсионный способ оценки изменчивости.

Дисперсионный анализ в Excel

Условно цель дисперсионного способа можно сконструировать так: вычленить из общей вариативности параметра 3 личные вариативности:

• 1 – определенную действием всякого из изучаемых значений;
• 2 – продиктованную связью меж исследуемыми значениями;
• 3 – случайную, продиктованную всеми неучтенными обстоятельствами.

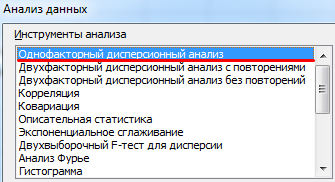
В программке Microsoft Excel дисперсионный анализ можно выполнить при помощи инструмента «Анализ данных» (вкладка «Данные» — «Анализ»). Это надстройка табличного микропроцессора. Если надстройка недосягаема, необходимо открыть «Характеристики Excel» и включить настройку для анализа.

Работа начинается с дизайна таблицы. Правила:

1. В любом столбце должны быть значения 1-го исследуемого фактора.
2. Столбцы расположить по возрастанию/убыванию величины исследуемого параметра.

Разглядим дисперсионный анализ в Excel на примере.

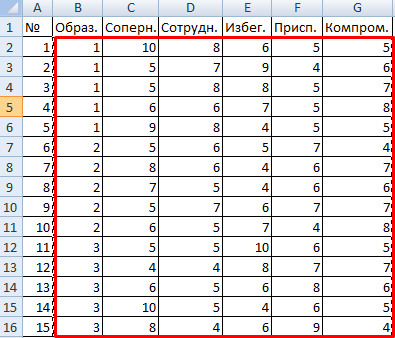
Психолог конторы проанализировал при помощи специальной методики стратегии поведения служащих в конфликтной ситуации. Предполагается, что на поведение влияет уровень образования (1 – среднее, 2 – среднее особое, 3 – высшее).

Внесем данные в таблицу Excel:

1. Открываем диалоговое окно нашего аналитического инструмента. В раскрывшемся перечне избираем «Однофакторный дисперсионный анализ» и жмем ОК.
2. В поле «Входной интервал» ввести ссылку на спектр ячеек, содержащихся во всех столбцах таблицы.
3. «Группирование» назначить по столбцам.
4. «Характеристики вывода» — новейший рабочий лист. Если необходимо указать выходной спектр на имеющемся листе, то переключатель ставим в положение «Выходной интервал» и ссылаемся на левую верхнюю ячейку спектра для выводимых данных. Размеры обусловятся автоматом.
5. Результаты анализа выводятся на отдельный лист (в нашем примере).

Весомый параметр залит желтоватым цветом. Потому что Р-Значение меж группами больше 1, аспект Фишера недозволено считать весомым. Как следует, поведение в конфликтной ситуации не зависит от уровня образования.

Факторный анализ в Excel: пример

Факторным именуют многомерный анализ взаимосвязей меж значениями переменных. При помощи данного способа можно решить важные задачки:

• всесторонне обрисовать измеряемый объект (при этом емко, компактно);
• выявить сокрытые переменные значения, определяющие наличие линейных статистических корреляций;
• систематизировать переменные (найти связи меж ними);
• уменьшить число нужных переменных.

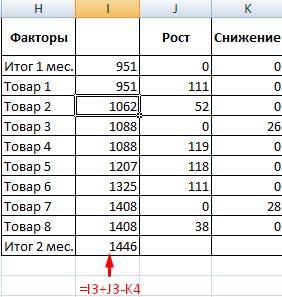
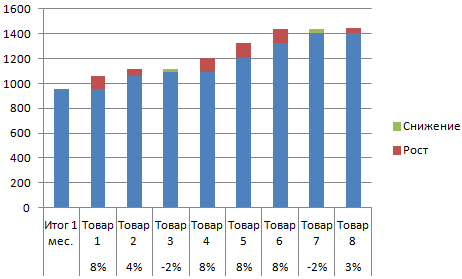
Разглядим на примере проведение факторного анализа. Допустим, нам известны реализации каких-то продуктов за крайние 4 месяца. Нужно проанализировать, какие наименования пользуются спросом, а какие нет.

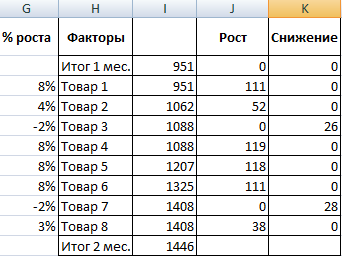
1. Поглядим, за счет, каких наименований произошел главный рост по итогам второго месяца. Если реализации какого-то продукта выросли, положительная дельта – в столбец «Рост». Отрицательная – «Понижение». Формула в Excel для «роста»: =ЕСЛИ((C2-B2)>0;C2-B2;0), где С2-В2 – разница меж 2 и 1 месяцем. Формула для «понижения»: =ЕСЛИ(J3=0;B2-C2;0), где J3 – ссылка на ячейку слева («Рост»). Во 2-м столбце – сумма предшествующего значения и предшествующего роста за вычетом текущего понижения.
2. Рассчитаем процент роста по любому наименованию продукта. Формула: =ЕСЛИ(J3/$I$11=0;-K3/$I$11;J3/$I$11). Где J3/$I$11 – отношение «роста» к итогу за 2 месяц, ;-K3/$I$11 – отношение «понижения» к итогу за 2 месяц.
3. Выделяем область данных для построения диаграммы. Перебегаем на вкладку «Вставка» — «Гистограмма».
4. Поработаем с подписями и цветами. Уберем накопительный результат через «Формат ряда данных» — «Заливка» («Нет заливки»). При помощи данного инвентаря меняем цвет для «понижения» и «роста».

Сейчас наглядно видно, реализации какого продукта дают главный рост.

Двухфакторный дисперсионный анализ в Excel

Указывает, как влияет два фактора на изменение значения случайной величины. Разглядим двухфакторный дисперсионный анализ в Excel на примере.

Задачка. Группе парней и дам предъявляли звук разной громкости: 1 – 10 дБ (Децибел — логарифмическая единица уровней, затуханий и усилений), 2 – 30 дБ (Децибел — логарифмическая единица уровней, затуханий и усилений), 3 – 50 дБ (Децибел — логарифмическая единица уровней, затуханий и усилений). Время ответа фиксировали в миллисекундах. Нужно найти, влияет ли пол на реакцию; влияет ли громкость на реакцию.

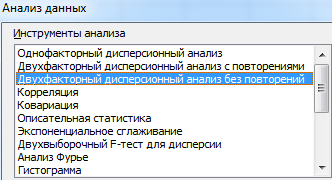
1. Перебегаем на вкладку «Данные» — «Анализ данных» Избираем из перечня «Двухфакторный дисперсионный анализ без повторений».
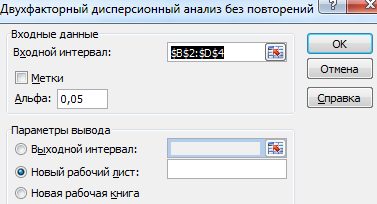
2. Заполняем поля. В спектр должны войти лишь числовые значения.
3. Итог анализа выводится на новейший лист (как было задано).

Та как F-статистики (столбец «F») для фактора «Пол» больше критичного уровня F-распределения (столбец «F-критическое»), данный фактор имеет воздействие на анализируемый параметр (время реакции на звук).