Цифровая сортировка
(англ. radix sort) — один из алгоритмов сортировки, использующих внутреннюю структуру сортируемых объектов.
Содержание
Метод [ править ]

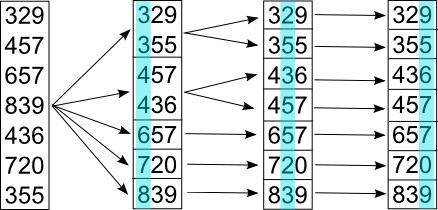
Имеем огромное количество последовательностей схожей длины, состоящих из частей, на которых задано отношение линейного порядка. Требуется отсортировать эти последовательности в словарном порядке.
По аналогии с разрядами чисел будем именовать элементы, из которых состоят сортируемые объекты, разрядами. Сам метод состоит в поочередной сортировке объектов какой-нибудь устойчивой сортировкой по любому уровню, в порядке от младшего разряда к старшему, опосля что последовательности будут размещены в требуемом порядке.
Примерами объектов, которые комфортно разбивать на разряды и сортировать по ним, являются числа и строчки.
- Для чисел уже существует понятие разряда, потому будем представлять числа как последовательности разрядов. Естественно, в различных системах счисления разряды 1-го и такого же числа различаются, потому перед сортировкой представим числа в комфортной для нас системе счисления.
- Строчки представляют из себя последовательности знаков, потому в качестве разрядов в данном случае выступают отдельные знаки, сопоставление которых обычно происходит по подходящим им кодам из таблицы шифровок. Для такового разбиения самый младший разряд — крайний знак строчки.
Для перечисленных выше объектов более нередко в качестве устойчивой сортировки используют сортировку подсчетом.
Таковой подход к методу именуют LSD-сортировкой (Least Significant Digit radix sort). Существует модификация метода цифровой сортировки, анализирующая значения разрядов, начиная слева, с более означающих разрядов. Данный метод известен, как MSD-сортировка (Most Significant Digit radix sort).
Правильность метода LSD-сортировки [ править ]
Докажем, что данный метод работает правильно, используя способ математической индукции по номеру разряда. Пусть [math] n [/math] — количество разрядов в сортируемых объектах.
База: [math] n = 1 [/math] . Разумеется, что метод работает правильно, поэтому что в таком случае мы просто сортируем младшие разряды некий заблаговременно избранной устойчивой сортировкой.
Переход: Пусть для [math] n = k [/math] метод верно отсортировал последовательности по [math] k [/math] младшим разрядам. Покажем, что в таком случае, при сортировке по [math] (k + 1) [/math] -му уровню, последовательности также будут отсортированы в правильном порядке.
Вспомогательная сортировка разобьет все объекты на группы, в которых [math] (k + 1) [/math] -й разряд объектов однообразный. Разглядим такие группы. Для сортировки по отдельным разрядам мы используем устойчивую сортировку, как следует порядок объектов с схожим [math] (k + 1) [/math] -м разрядом не поменялся. Но по предположению индукции по предшествующим [math] k [/math] разрядам последовательности были отсортированы верно, и потому в каждой таковой группе они будут отсортированы правильно. Также правильно, что сами группы находятся в правильном относительно друг дружку порядке, а, как следует, и все объекты отсортированы верно по [math] (k + 1) [/math] -м младшим разрядам.
Псевдокод [ править ]
LSD-сортировка [ править ]
В качестве примера разглядим сортировку чисел. Как говорилось выше, в таковой ситуации в качестве устойчивой сортировки используют сортировку подсчетом, потому что обычно количество разных значений разрядов не превосходит количества сортируемых частей. Ниже приведен псевдокод цифровой сортировки, которой подается массив [math] A [/math] размера [math] n [/math] [math] m [/math] -разрядных чисел . Сам по для себя метод представляет собой цикл по номеру разряда, на каждой итерации которого элементы массива [math] A [/math] располагаются в подходящем порядке во вспомогательном массиве [math] B [/math] . Для подсчета количества объектов, [math] i [/math] -й разряд которых однообразный, а потом и для определения положения объектов в массиве [math] B [/math] употребляется вспомогательный массив [math] C [/math] . Функция [math] mathrm
MSD-сортировка [ править ]
Будем считать, что у всех частей однообразное число разрядов. Если это не так, то положим на наиболее старших разрядах элементы с самым небольшим значением — для чисел это [math]0[/math] . Поначалу начальный массив делится на [math]k[/math] частей, где [math]k[/math] — основание, выбранное для представления сортируемых объектов. Эти части принято именовать «корзинами» либо «кармашками». В первую корзину попадают элементы, у каких старший разряд с номером [math]d = 0[/math] имеет значение [math]0[/math] . Во вторую корзину попадают элементы, у каких старший разряд с номером [math]d = 0[/math] имеет значение [math]1[/math] и так дальше. Потом элементы, попавшие в различные корзины, подвергаются рекурсивному разделению по последующему уровню с номером [math]d = 1[/math] . Рекурсивный процесс разделения длится, пока не будут перебраны все разряды сортируемых объектов и пока размер корзины больше единицы. Другими словами останавливаемся когда [math]d gt m[/math] либо [math]l geqslant r[/math] , где m — наибольшее число разрядов в сортируемых объектах, [math]l[/math] , [math]r[/math] — левая и правая границы отрезка массива [math]A[/math] .
В базу распределения частей по корзинам положен способ распределяющего подсчета частей с схожими значениями в сортируемом разряде. Для этого производится просмотр массива и подсчет количества частей с разными значениями в сортируемом разряде. Эти счетчики фиксируются во вспомогательном массиве счетчиков [math]cnt[/math] . Потом счетчики употребляются для вычисления размеров корзин и определения границ разделения массива. В согласовании с этими границами сортируемые объекты переносятся во вспомогательный массив [math]c[/math] , в котором расположены корзины. Опосля того как корзины сформированы, содержимое вспомогательного массива [math]c[/math] переносится назад в начальный массив [math]A[/math] и производится рекурсивное разделение новейших частей по последующему уровню в границах границ корзин, приобретенных на прошлом шаге.
Вначале запускаем функцию так [math]mathrm
Сложность [ править ]
Сложность LSD-сортировки [ править ]
Пусть [math] m [/math] — количество разрядов, [math] n [/math] — количество объектов, которые необходимо отсортировать, [math] T(n) [/math] — время работы устойчивой сортировки. Цифровая сортировка делает [math] k [/math] итераций, на каждой из которой производится устойчивая сортировка и не наиболее [math] O(1) [/math] остальных операций. Как следует время работы цифровой сортировки — [math] O(k T(n)) [/math] .
Разглядим раздельно вариант сортировки чисел. Пусть в качестве аргумента сортировке передается массив, в котором содержатся [math] n [/math] [math] m [/math] -значных чисел, и любая цифра может принимать значения от [math] 0 [/math] до [math] k — 1 [/math] . Тогда цифровая сортировка дозволяет отсортировать данный массив за время [math] O(m (n + k)) [/math] , если устойчивая сортировка имеет время работы [math] O(n + k) [/math] . Если [math] k [/math] маленькое, то нормально выбирать в качестве устойчивой сортировки сортировку подсчетом.
Если количество разрядов — константа, а [math] k = O(n) [/math] , то сложность цифровой сортировки составляет [math] O(n) [/math] , другими словами она линейно зависит от количества сортируемых чисел.
Сложность MSD-сортировки [ править ]
Пусть значения разрядов меньше [math]b[/math] , а количество разрядов — [math]k[/math] . При сортировке массива из схожих частей MSD-сортировкой на любом шаге все элементы будут находится в неубывающей по размеру корзине, а потому что цикл идет по всем элементам массива, то получим, что время работы MSD-сортировки оценивается величиной [math]O(nk)[/math] , при этом это время недозволено сделать лучше. Неплохим случаем для данной сортировки будет массив, при котором на любом шаге любая корзина будет делиться на [math]b[/math] частей. Как размер корзины станет равен [math]1[/math] , сортировка не станет рекурсивно запускаться в данной нам корзине. Таковым образом, асимптотика будет [math]Omega(nlog_b
Существует также модификация MSD-сортировки, при которой рекурсивный процесс останавливается при маленьких размерах текущего кармашка, и вызывается наиболее стремительная сортировка, основанная на сопоставлениях (к примеру, сортировка вставками).